浅谈AVL树

文章目录

  • 1.介绍
    • 1.1定义
    • 1.2来源
    • 1.3概念
      • 1.特性
      • 2.平衡因子[ Balance Factor-- _bf ]
  • 2.BST==>AVL
    • 1.示例分析
    • 2.情况分类
    • 3.代码剖析
      • 3.1左左型-右单旋
      • 3.2右右型-左单旋
      • 3.3左右型-左右旋
      • 3.4右左型:右左旋
      • 3.5总图
  • 3.完整代码
    • 3.1AVLTree.h
    • 3.2Test.cpp

在这里插入图片描述

1.介绍

1.1定义

AVL树 – 平衡二叉树 – 平衡二叉搜索（排序）树 – 高度平衡搜索树
Balanced Binary Tree （BBT）

1.2来源

AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。
二叉搜索树可以缩短查找的效率，但在数据有序或接近有序时它将退化为单支树，查找元素相当于在顺序表中搜索，效率低下。两位俄罗斯的数学家发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

1.3概念

1.特性

  • 一棵空树或左右两个子树高度差绝对值不超过1
  • 左右两个子树也都是一棵高度平衡搜索树

2.平衡因子[ Balance Factor-- _bf ]

  1. 结点的平衡因子 == 右子树高度 - 左子树高度
  2. | _bf | <= 1
  3. AVL树不一定有平衡因子, 使用平衡因子只是一种较为简单的实现方式
    在这里插入图片描述

2.BST==>AVL

[设定 _bf = 右子树高度 - 左子树高度]

1.示例分析

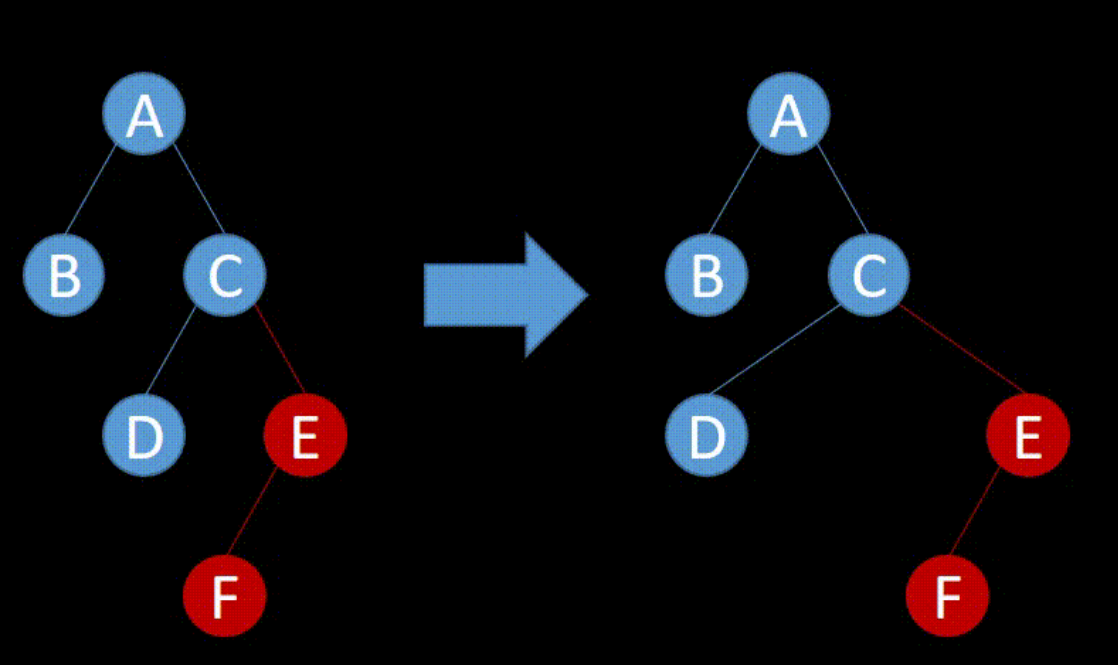
先看一下下面的图 了解一下什么叫做旋转 以及旋转的目的

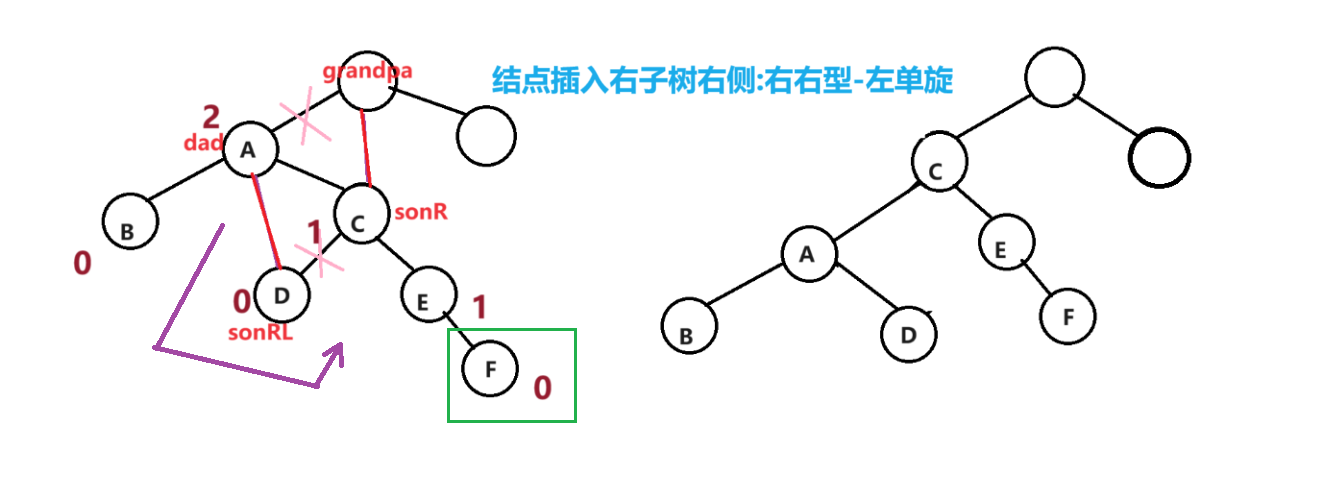
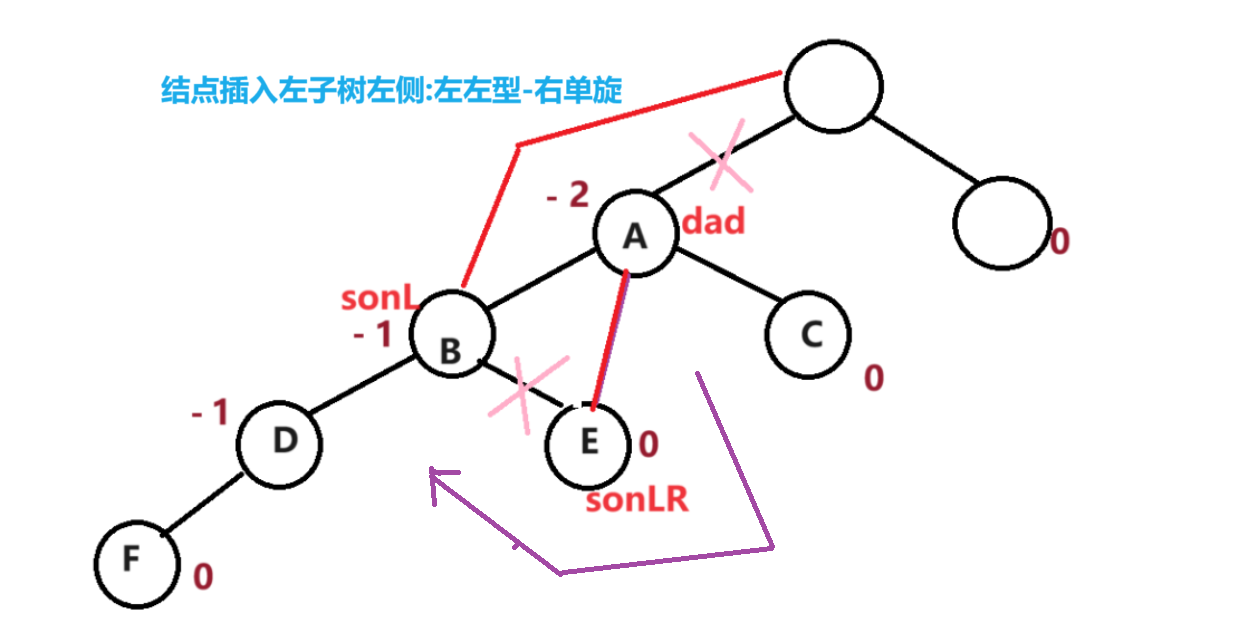
在这里插入图片描述
在这里插入图片描述

2.情况分类

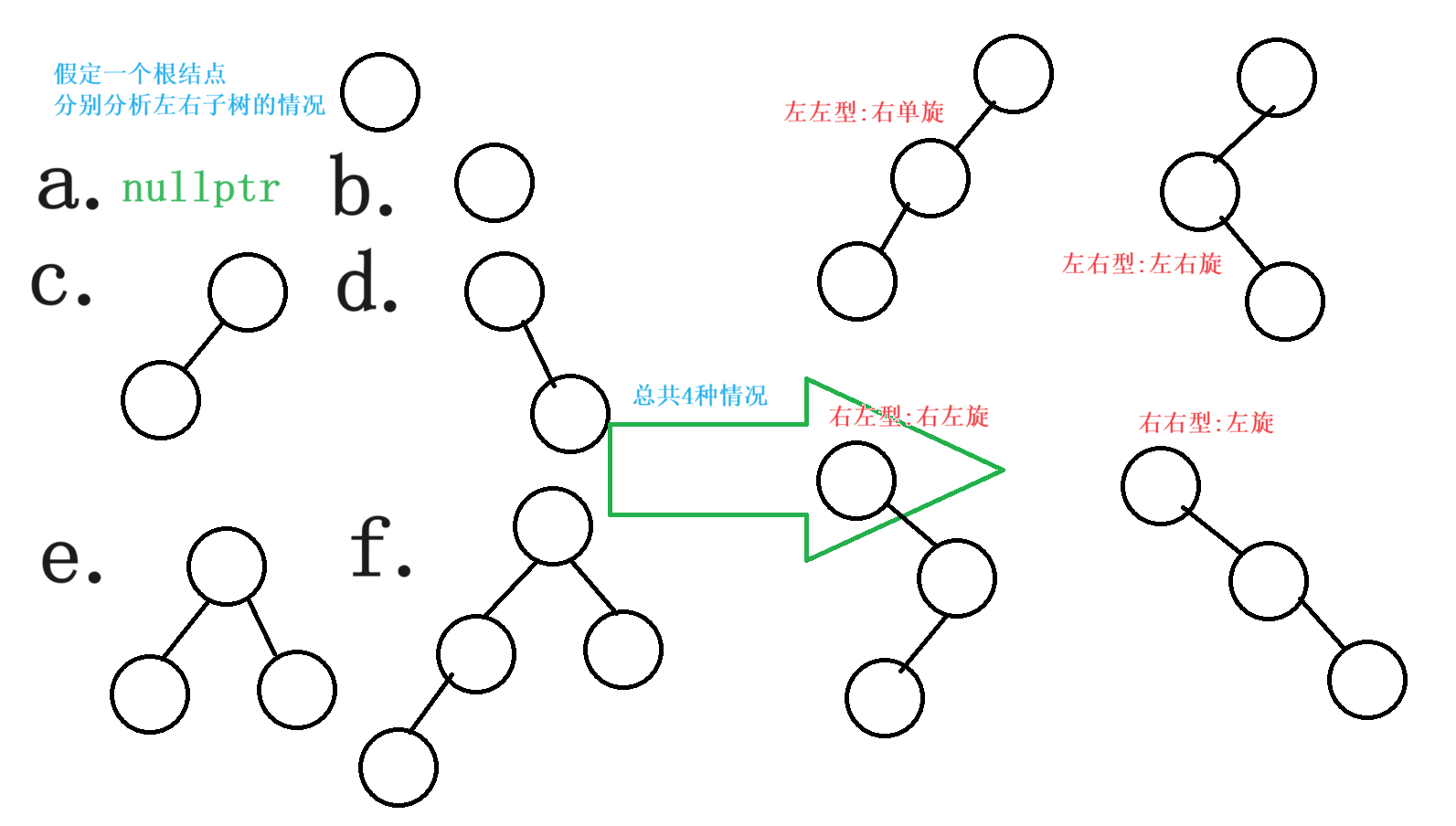
在这里插入图片描述

3.代码剖析

3.1左左型-右单旋

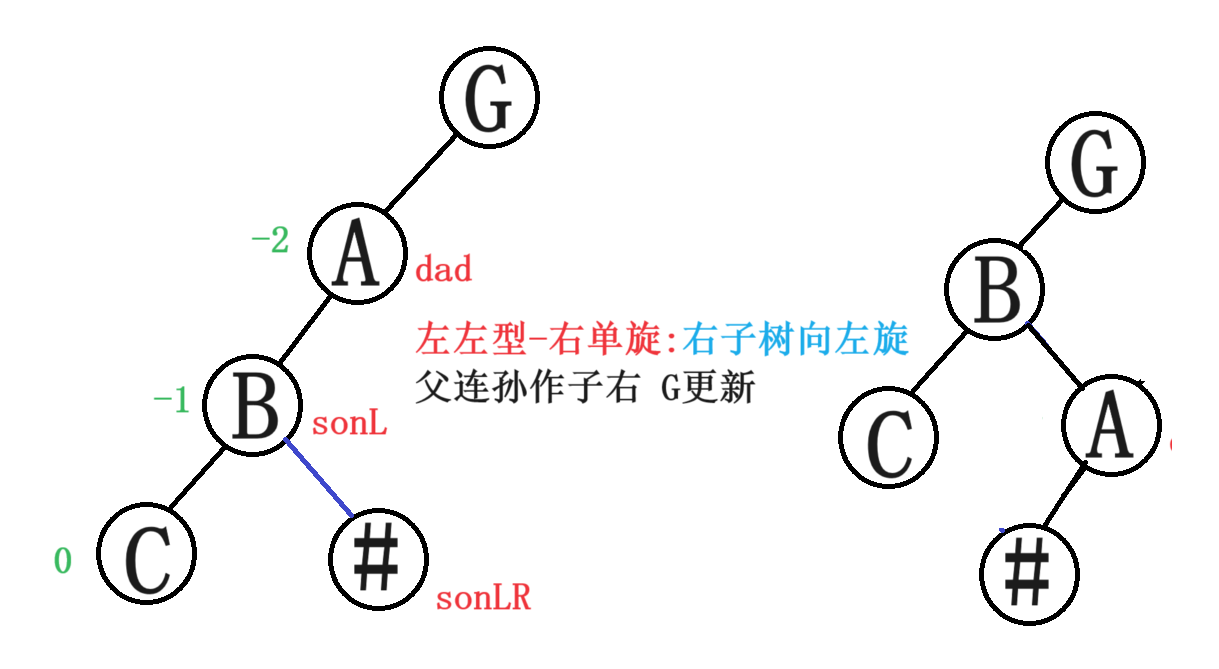
在这里插入图片描述

	void RotateRight(Node* dad){Node* Grandpa = dad->_parent;Node* sonL = dad->_left;Node* sonLR = sonL->_right;//dad连接sonLR sonLR不空-继承dad 为空不继承dad->_left = sonLR;if (sonLR)sonLR->_parent = dad;//sonL连接dad dad继承sonLsonL->_right = dad;dad->_parent = sonL;//G为空 表明dad为根结点 if (Grandpa == nullptr){//更新根结点_root = sonL;//更新根结点成员属性_root->_parent = nullptr;}else{//父连子if (Grandpa->_left == dad)Grandpa->_left = sonL;elseGrandpa->_right = sonL;//子继承父sonL->_parent = Grandpa;}//更新_bfsonL->_bf = dad->_bf = 0;}

3.2右右型-左单旋

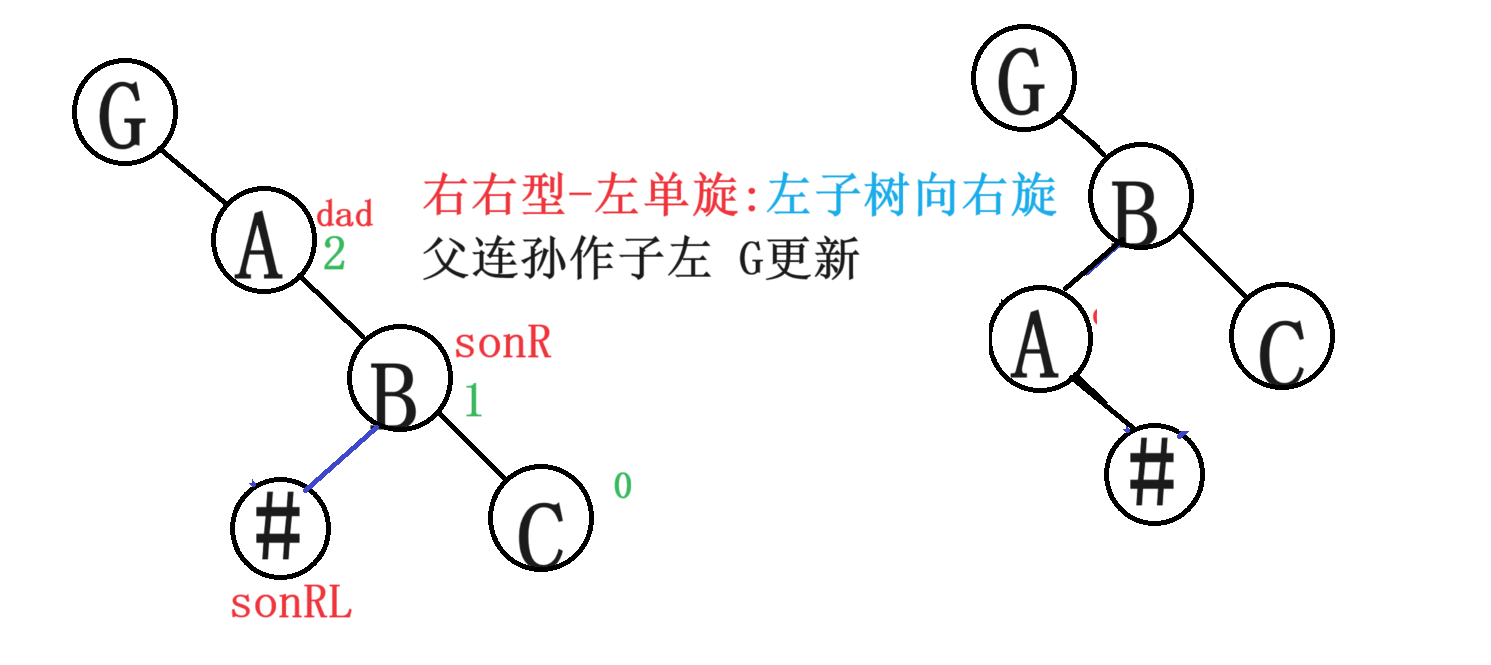
在这里插入图片描述

void RotateLeft(Node* dad)
{Node* Grandpa = dad->_parent;Node* sonR = dad->_right;Node* sonRL = sonR->_left;//dad连接sonRL sonRL不空继承dad 为空不继承dad->_right = sonRL;if (sonRL)sonRL->_parent = dad;//sonR连接dad dad继承sonRsonR->_left = dad;dad->_parent = sonR;//Grandpa为空--dad为根节点 更新后 sonR为根节点 根节点的_parent置空if (Grandpa == nullptr){_root = sonR;_root->_parent = nullptr;}//不为空 依实际连接else{//父连子if (Grandpa->_left == dad)Grandpa->_left = sonR;elseGrandpa->_right = sonR;//子继承父sonR->_parent = Grandpa;}//左旋目的达到 更新_bfdad->_bf = sonR->_bf = 0;
}

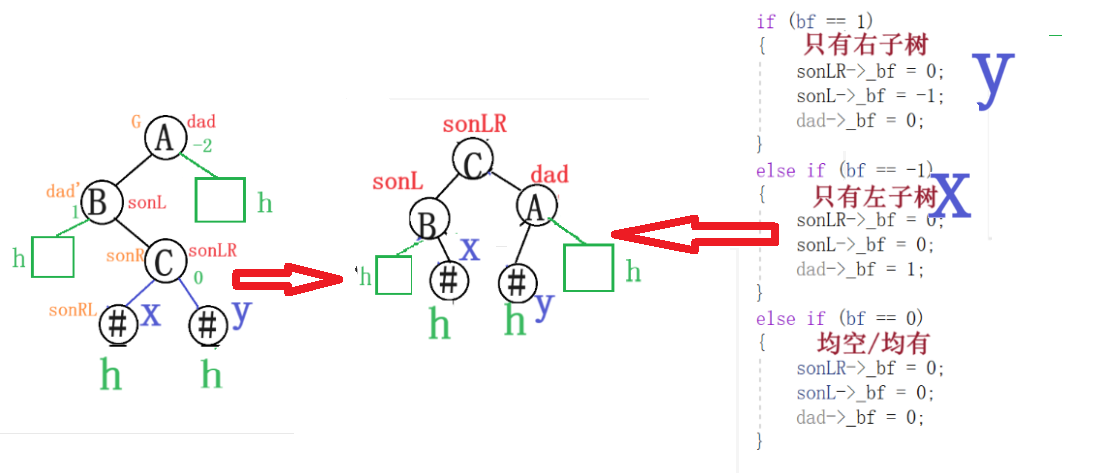
3.3左右型-左右旋

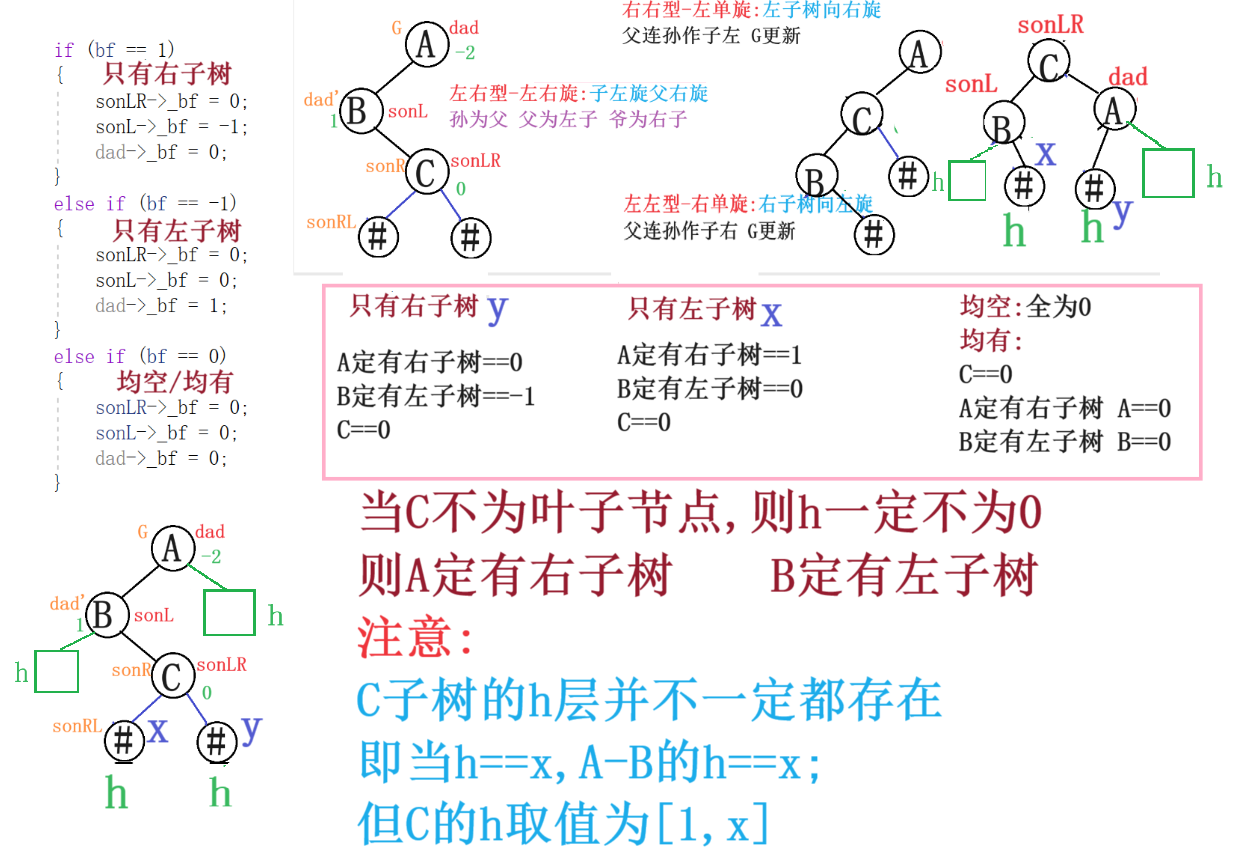
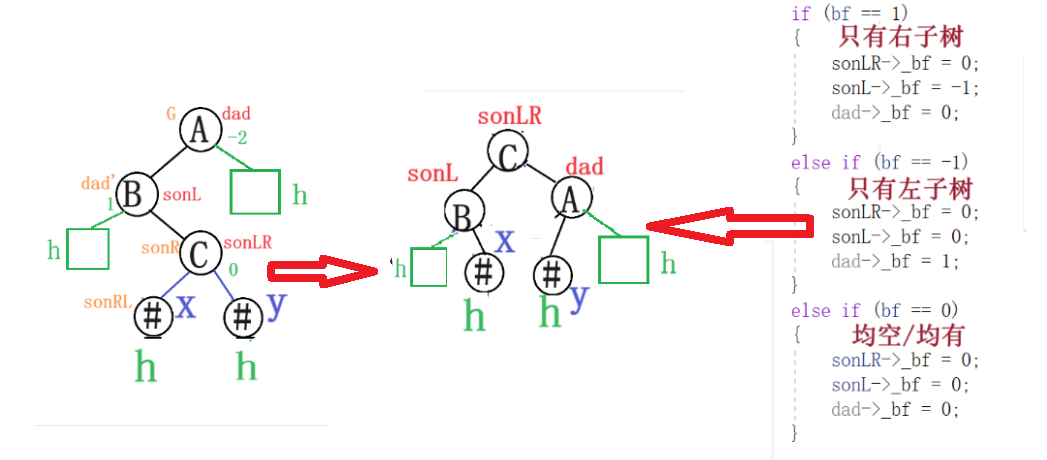
在这里插入图片描述
在这里插入图片描述

void RotateLR(Node* dad)
{Node* sonL = dad->_left;Node* sonLR = sonL->_right;int bf = sonLR->_bf;RotateLeft(sonL);RotateRight(dad);if (bf == 1){sonLR->_bf = 0;sonL->_bf = -1;dad->_bf = 0;}else if (bf == -1){sonLR->_bf = 0;sonL->_bf = 0;dad->_bf = 1;}else if (bf == 0){sonLR->_bf = 0;sonL->_bf = 0;dad->_bf = 0;}else{assert(false);}
}

3.4右左型:右左旋

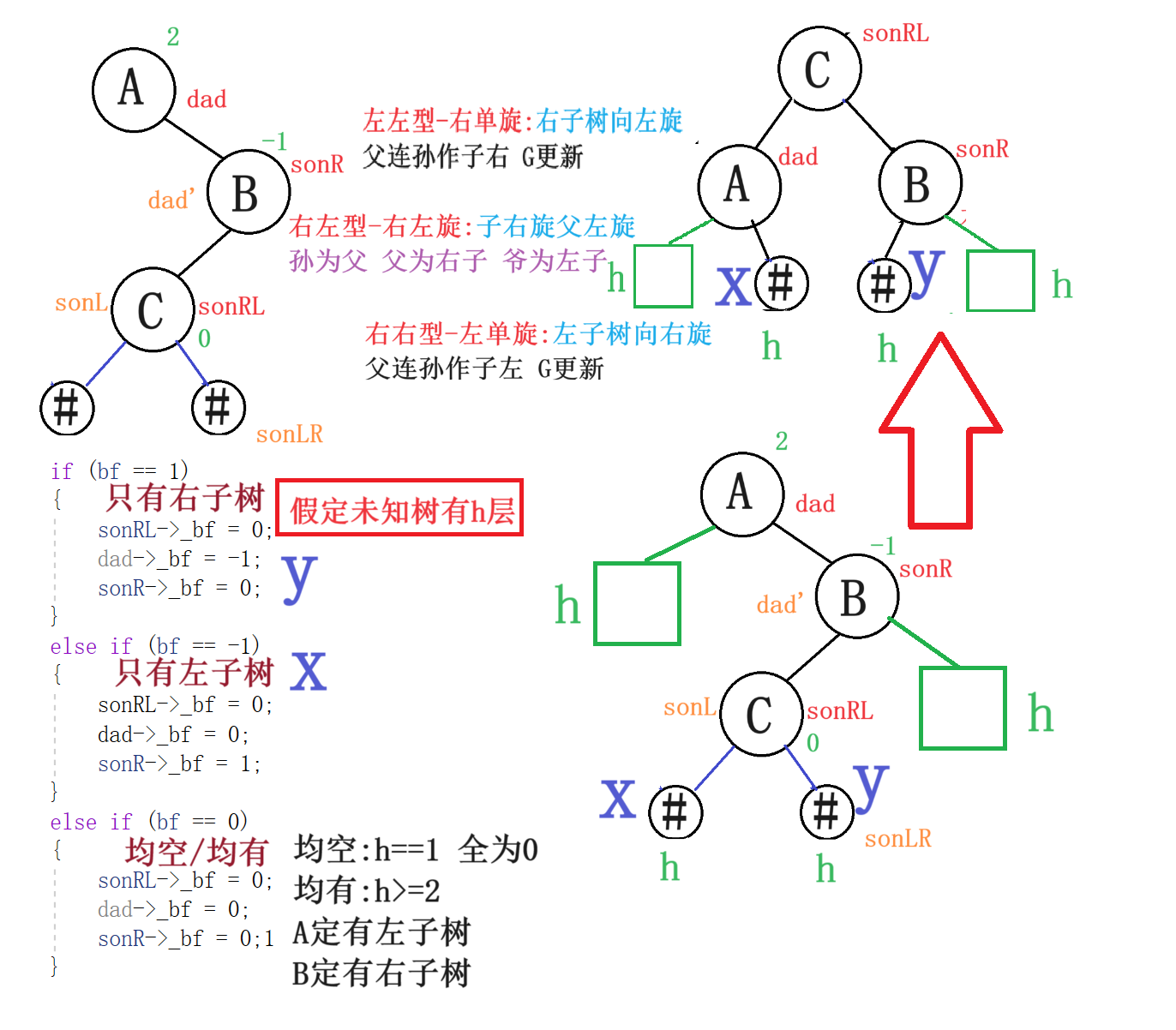
在这里插入图片描述
在这里插入图片描述

void RotateRL(Node* dad)
{Node* sonR = dad->_right;Node* sonRL = sonR->_left;int bf = sonRL->_bf;//最终根结点的_bfRotateLeft(dad->_right);RotateRight(dad);if (bf == 1){sonRL->_bf = 0;dad->_bf = -1;sonR->_bf = 0;}else if (bf == -1){sonRL->_bf = 0;dad->_bf = 0;sonR->_bf = 1;}else if (bf == 0){sonRL->_bf = 0;dad->_bf = 0;sonR->_bf = 0;1}else{assert(false);}
}

3.5总图

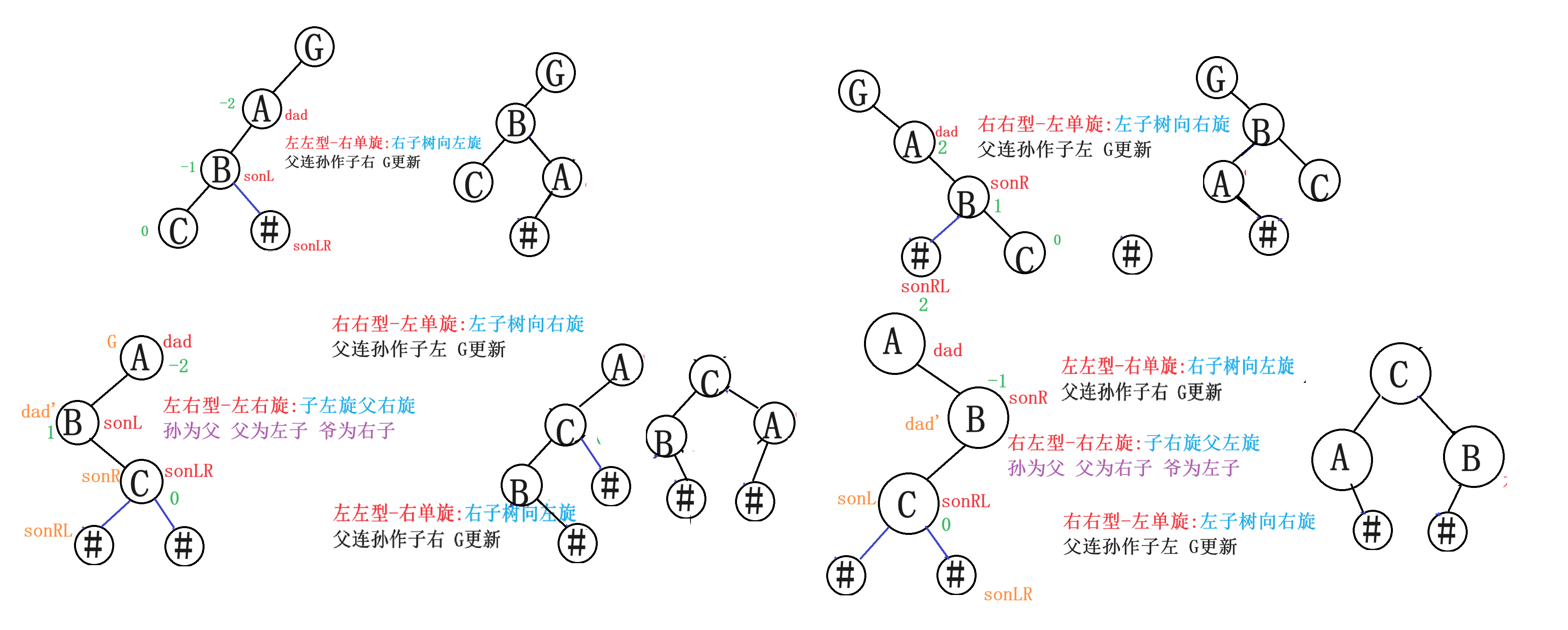
在这里插入图片描述

3.完整代码

3.1AVLTree.h

#pragma once
#include <iostream>
#include <list>
#include <vector>
#include <algorithm>
#include <array>
#include <time.h>
#include <queue>
#include <stack>
#include <string>
#include <set>
#include <map>
#include <functional>
#include <assert.h>
#include <math.h>
using namespace std;
template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _pair;int _bf;           // balance factorAVLTreeNode(const pair<K, V>& pair):_left(nullptr), _right(nullptr), _parent(nullptr), _pair(pair), _bf(0){}
};//高度平衡搜索树
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public://插入--创建二叉树bool Insert(const pair<K, V>& pair){//空树--new结点if (_root == nullptr){_root = new Node(pair);return true;}//非空--插入//1.定位到合适位置Node* parent = nullptr;Node* cp = _root;while (cp){if (pair.first > cp->_pair.first){parent = cp;cp = cp->_right;}else if (pair.first < cp->_pair.first){parent = cp;cp = cp->_left;}else{//搜索树不可有数据重复 -- 插入失败return false;}}//2.链接cp = new Node(pair);if (pair.first < parent->_pair.first){parent->_left = cp;}else{parent->_right = cp;}//cp继承parentcp->_parent = parent;//构建AVL树while (parent){//一、更新平衡因子//插入结点在右子树if (cp == parent->_right){parent->_bf++;}//插入结点在左子树else{parent->_bf--;}//二、分类讨论// _bf == 1/-1 原为0 现高度受到影响// 回溯直至遇到根源结点 即_bf==2/-2的结点if (parent->_bf == 1 || parent->_bf == -1){parent = parent->_parent;cp = cp->_parent;}//_bf == 0 不做处理 原为-1/1 现已满足 不继续更新else if (parent->_bf == 0){break;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转处理目的://1.使得当前子树平衡 2.降低当前子树的高度//左单旋if (parent->_bf == 2 && cp->_bf == 1){RotateL(parent);}//右单旋else if (parent->_bf == -2 && cp->_bf == -1){RotateR(parent);}//左右旋else if (parent->_bf == -2 && cp->_bf == 1){RotateLR(parent);}//右左旋else if (parent->_bf == 2 && cp->_bf == -1){RotateRL(parent);}else{assert(false);}break;}else{assert(false);}}return true;}//中序遍历void InOrder(){_InOrder(_root);cout << endl;}//高度接口int Height(){return _Height(_root);}//判断是否满足AVL树平衡bool IsBalance(){return _IsBalance(_root);}private:// 中序遍历void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_pair.first << " ";_InOrder(root->_right);}//高度接口int _Height(Node* root){if (root == NULL)return 0;int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;}//判断是否满足AVL树平衡bool _IsBalance(Node* root){if (root == NULL){return true;}int leftH = _Height(root->_left);int rightH = _Height(root->_right);if (rightH - leftH != root->_bf){cout << root->_pair.first << "Abnormal node balance factor!" << endl;return false;}return abs(leftH - rightH) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);}//左单旋void RotateL(Node* parent){//记录GrandpaNode* Grandpa = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;//parent链接subRL subRL不空继承parent 空没必要继承parent->_right = subRL;if (subRL)subRL->_parent = parent;//subR连接parent parent继承subRsubR->_left = parent;parent->_parent = subR;//Grandpa为空--parent为根节点 更新后 subR为根节点 根节点的_parent置空if (Grandpa == nullptr){_root = subR;_root->_parent = nullptr;}//不为空 依实际连接else{//父连子if (Grandpa->_left == parent){Grandpa->_left = subR;}else{Grandpa->_right = subR;}//子继承父subR->_parent = Grandpa;}parent->_bf = subR->_bf = 0;}//右单旋void RotateR(Node* parent){Node* Grandpa = parent->_parent;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (Grandpa->_left == parent){Grandpa->_left = subL;}else{Grandpa->_right = subL;}subL->_parent = Grandpa;}subL->_bf = parent->_bf = 0;}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else if (bf == -1){parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf == 0){parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else{assert(false);}}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 1){subR->_bf = 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 0){subR->_bf = 0;parent->_bf = 0;subRL->_bf = 0;}else{assert(false);}}private:Node* _root = nullptr;
};void Test_AVLTree1()
{int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int b[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };AVLTree<int, int> tree;for (auto e : b){tree.Insert(make_pair(e, e));if (tree.IsBalance()){cout << e << "插入成功!" << endl;}else{cout << e << "插入失败!" << endl;}}cout << "此树中序遍历:" << endl;tree.InOrder();if (tree.IsBalance()){cout << "此树为一棵AVL树" << endl;}else{cout << "此树不为一棵AVL树!" << endl;}
}void Test_AVLTree2()
{srand(time(0));const size_t N = 10;AVLTree<int, int> tree;for (size_t i = 0; i < N; ++i){size_t x = rand() + i;tree.Insert(make_pair(x, x));if (tree.IsBalance()){cout << x << "插入成功!" << endl;}else{cout << x << "插入失败!" << endl;}}cout << "此树中序遍历:" << endl;tree.InOrder();if (tree.IsBalance()){cout << "此树为一棵AVL树" << endl;}else{cout << "此树不为一棵AVL树!" << endl;}cout << "此树高度为:" << tree.Height() << endl;
}

3.2Test.cpp

#define _CRT_SECURE_NO_WARNINGS 
#include <iostream>
#include <list>
#include <vector>
#include <algorithm>
#include <array>
#include <time.h>
#include <queue>
#include <stack>
#include <string>
#include <set>
#include <map>
#include <functional>
using namespace std;
#include "AVLTree.h"int main()
{Test_AVLTree1();return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/90980.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

RabbitMQ（15672） 消息中间件 NOTE

RabbitMQ（15672） 消息中间件 NOTE

目录 1、初识 RabbitMQ 消息队列 1.1 MQ 四大核心概念 1.2 消息的发送&#xff08;无交换机态&#xff09; 1.3 关于消息自动重新入队 1.3.1 消息的常见应答方法&#xff08;R&#xff09; 1.4 关于 RabbitMQ 的持久化、不公平分发以及预取值 2、RabbitMQ 消息的发布确认…
阅读更多...
centos7用docker安装WireGuard教程

centos7用docker安装WireGuard教程

PS:本文章用于帮助组建自己内网或者公司组网操作,该教程不涉及翻墙操作. 1、 检查centos内核版本 uname -r2、升级内核 下载脚本上传到服务器运行脚本进行升级内核 链接&#xff1a;https://pan.baidu.com/s/1vYmqVy2St3nFnJWGPIwdOw 提取码&#xff1a;owac 3、安装WireG…
阅读更多...
云原生Kubernetes：K8S安全机制

云原生Kubernetes：K8S安全机制

目录 一、理论 1.K8S安全机制 2.Authentication认证 3.Authorization授权 4.Admission Control准入控制 5.User访问案例 6.ServiceAccount访问案例 二、实验 1.Admission Control准入控制 2.User访问案例 3.ServiceAccount访问案例 三、问题 1.生成资源报错 2.镜…
阅读更多...
uniapp瀑布流：他的数据是纵向渲染，怎么实现动态上拉加载数据？

uniapp瀑布流：他的数据是纵向渲染，怎么实现动态上拉加载数据？

不喜勿喷&#xff0c;非常感谢 准备数据&#xff1a;首先&#xff0c;你需要有一些数据&#xff0c;这些数据将会在瀑布流中渲染。你可以将这些数据存储在一个数组中&#xff0c;或者从服务器请求获取。 创建页面&#xff1a;在UniApp中创建一个页面&#xff0c;用于展示纵向…
阅读更多...
7.2 怎样定义函数

7.2 怎样定义函数

7.2.1 为什么要定义函数 主要内容&#xff1a; 为什么要定义函数 C语言要求所有在程序中用到的函数必须“先定义&#xff0c;后使用”。这是因为在调用一个函数之前&#xff0c;编译系统需要知道这个函数的名字、返回值类型、功能以及参数的个数与类型。如果没有事先定义&…
阅读更多...
多叉树+图实现简单业务流程

多叉树+图实现简单业务流程

文章目录 场景整体架构流程业务界面技术细节小结 场景 这次遇到一个需求,大致就是任务组织成方案,方案组织成预案,预案可裁剪调整.预案关联事件等级配置,告警触发预案产生事件.然后任务执行是有先后的,也就是有流程概念. 整体架构流程 方案管理、预案管理构成任务流程的基础条…
阅读更多...
k8s-实战——基于nfs实现动态存储

k8s-实战——基于nfs实现动态存储

部署nfs服务 基于Centos7.9版本创建动态存储注意k8s版本应低于v1.24版本高k8s版本ServiceAccount需要手动创建secrets并关联相关sa部署流程 创建NFS共享服务、采用单独的节点用于nfs服务独占安装nfs-utils和rpcbindnfs客户端和服务端都安装nfs-utils包通过部署化脚本安装k8s集群…
阅读更多...
nginx 多层代理 + k8s ingress 后端服务获取客户真实ip 配置

nginx 多层代理 + k8s ingress 后端服务获取客户真实ip 配置

1.nginx http 七层代理 修改命令空间&#xff1a; namespace: nginx-ingress : configmap&#xff1a;nginx-configuration kubectl get cm nginx-configuration -n ingress-nginx -o yaml添加如上配置 compute-full-forwarded-for: “true” forwarded-for-header: X-Forwa…
阅读更多...
java通过接口转发文件（上传下载）

java通过接口转发文件（上传下载）

java接口转发上传的文件 RequestMapping(value "/XXXX/fileUpload", method RequestMethod.POST) public String getFileUpload2(RequestParam("file") MultipartFile file, HttpServletRequest request) public static String hotMapPost3(String ur…
阅读更多...
.balckhoues-V-XXXXXXX勒索病毒数据怎么处理|数据解密恢复

.balckhoues-V-XXXXXXX勒索病毒数据怎么处理|数据解密恢复

引言&#xff1a; 随着网络犯罪的不断演进&#xff0c;勒索病毒已成为当前数字时代的威胁之一&#xff0c;其中包括.balckhoues-V-XXXXXXX勒索病毒。本文将深入介绍.balckhoues-V-XXXXXXX勒索病毒的特点、数据恢复方法以及预防措施&#xff0c;以帮助您更好地理解和应对这一威…
阅读更多...
pyqt实现简易浏览器

pyqt实现简易浏览器

需要的软件包如下&#xff1a; Package Version ----------------- ------- pip 23.2.1 PyQt5 5.15.9 PyQt5-Qt5 5.15.2 PyQt5-sip 12.12.2 PyQtWebEngine 5.15.6 PyQtWebEngine-Qt5 5.15.2 setuptools 65.5.1…
阅读更多...
NPDP产品经理认证怎么报名？考试难度大吗？

NPDP产品经理认证怎么报名？考试难度大吗？

PMDA&#xff08;Product Development and Management Association&#xff09;是美国产品开发与管理协会&#xff0c;在中国由中国人才交流基金会培训中心举办NPDP&#xff08;New Product Development Professional&#xff09;考试&#xff0c;该考试是产品经理国际资格认证…
阅读更多...
Spring实例化源码解析之ComponentScanAnnotationParser(四)

Spring实例化源码解析之ComponentScanAnnotationParser(四)

上一章我们分析了ConfigurationClassParser&#xff0c;配置类的解析源码分析。在ComponentScans和ComponentScan注解修饰的候选配置类的解析过程中&#xff0c;我们需要深入的了解一下ComponentScanAnnotationParser的parse执行流程&#xff0c;SpringBoot启动类为什么这么写&…
阅读更多...
WinPcap4.1.3安装失败解决方法，A newer version of winpcap...

WinPcap4.1.3安装失败解决方法，A newer version of winpcap...

WinPcap4.1.3安装失败解决方法&#xff0c;A newer version of winpcap… 如图所示&#xff0c;提示本地安装有更高版本的WinPcap时&#xff0c;按如下操作即可解决。 找到相应文件&#xff0c;扩展名修改成如下&#xff1a; C:\Windows\SysWOW64 的wpcap.dll改成 wpcap.dll.…
阅读更多...
tomcat乱码解决

tomcat乱码解决

解决乱码 1、修改bin\catalina.bat配置文件 修改tomcat的配置文件&#xff0c;找到tomcat路径下的\bin目录下的catalina.bat文件&#xff0c;修改 set “JAVA_OPTS%JAVA_OPTS% %JSSE_OPTS% -Dfile.encodingUTF-8 -Dsun.jnu.encodingUTF-8 ” 2、修改conf\logging.properties配置…
阅读更多...
【Verilog 教程】6.5 Verilog避免Latch

【Verilog 教程】6.5 Verilog避免Latch

关键词&#xff1a;触发器&#xff0c;锁存器 Latch 的含义 锁存器&#xff08;Latch&#xff09;&#xff0c;是电平触发的存储单元&#xff0c;数据存储的动作取决于输入时钟&#xff08;或者使能&#xff09;信号的电平值。仅当锁存器处于使能状态时&#xff0c;输出才会随着…
阅读更多...
使用 Velocity 模板引擎的 Spring Boot 应用

使用 Velocity 模板引擎的 Spring Boot 应用

使用 Velocity 模板引擎的 Spring Boot 应用 模板引擎是构建动态内容的重要工具&#xff0c;特别适用于生成HTML、邮件内容、报告和其他文本文档。Velocity是一个强大的模板引擎&#xff0c;它具有简单易用的语法和灵活性。本文将介绍如何在Spring Boot应用中使用Velocity模板…
阅读更多...
erlang练习题(三)

erlang练习题(三)

题目一 查询列表A是否为列表B的前缀 解答 isPrefix([], List2) -> io:format("A is prefix of B ~n");isPrefix([H1 | ListA], [H2 | ListB]) ->case H1 H2 oftrue -> isPrefix(ListA, ListB);false -> io:format("A is not prefix of B ~n&quo…
阅读更多...
[React] react-router-dom的v5和v6

[React] react-router-dom的v5和v6

v5 版本既兼容了类组件&#xff08;react v16.8前&#xff09;&#xff0c;又兼容了函数组件&#xff08;react v16.8及以后&#xff0c;即hook&#xff09;。v6 文档把路由组件默认接受的三个属性给移除了&#xff0c;若仍然使用 this.props.history.push()&#xff0c;此时pr…
阅读更多...
C语言入门Day_27 开发环境

C语言入门Day_27 开发环境

前言&#xff1a; 在线编译环境涉及到联网&#xff0c;如果在没有网的情况下&#xff0c;我们就不能写代码了&#xff0c;这一章节&#xff0c;我们将会给大家介绍一下如何搭建一个本地的C语言编译环境。 如果想要设置 C 语言环境&#xff0c;需要确保电脑上有以下两款可用的…
阅读更多...
最新文章

Copyright @ 2022~2023