[Leetcode小记] 3233. 统计不是特殊数字的数字数量

代码：

方法一：平凡解法(最直观但时间复杂度最高)

class Solution {public int nonSpecialCount(int l, int r) {int res=r-l+1;//初始不是特殊数字的答案为[l,r]范围内数字总数for(int i=(int)Math.ceil(Math.sqrt(l));i<=(int)Math.floor(Math.sqrt(r));i++){if(isPrime(i)) res--;//如果是质数，说明是特殊数字，则不是特殊数字的数-1}return res;}private boolean isPrime(int number){//判断数字是否是质数if(number==1) return false;if(number==2) return true;for(int i=2;i<=(int)Math.sqrt(number);i++){if(number%i==0) return false;}return true;}
}

时间复杂度：对于 nonSpecialCount 方法中的每个i，isPrime 方法被调用一次，其时间复杂度为 $O(\sqrt{i})$ ，由于 i 的范围是 $\left \lceil \sqrt{l} \right \rceil$ 到 $\left \lfloor \sqrt{r} \right \rfloor$ ，需要计算这些调用的总时间复杂度。

在最坏情况下，当 l=1 且 r 非常大时，nonSpecialCount 方法的时间复杂度主要由以下部分组成：

①循环次数：最多 $\sqrt{r}$ 次；②每次循环中调用 isPrime 的时间复杂度为 $O(\sqrt{i})$ ，其中i最大值为 $\sqrt{r}$ 。因此，总时间复杂度可以近似为： $\sum_{i=\sqrt{l}}^{\sqrt{r}}O(\sqrt{i})$ 。由于 $\sqrt{i}$ 是递增的，并且主要关心的是当 r 非常大时的行为，这个求和可以近似为： $O(\sqrt{r})*O(\sqrt{\sqrt{r}})=O(\sqrt{r}*r_{}^{1/4})=O(r_{}^{3/4})$ ，其中 r 是给定的区间上界。(注：该计算为较宽松的估计，实际上由于 i 的增长速度较慢，并且并不是对每一个 i 都进行到 $\sqrt{r}$ 的检查（而是到 $\sqrt{i}$ ），实际运行时间可能会比该估计要快。但从理论上看，该估计给出了一个上界。)

空间复杂度：O(1)

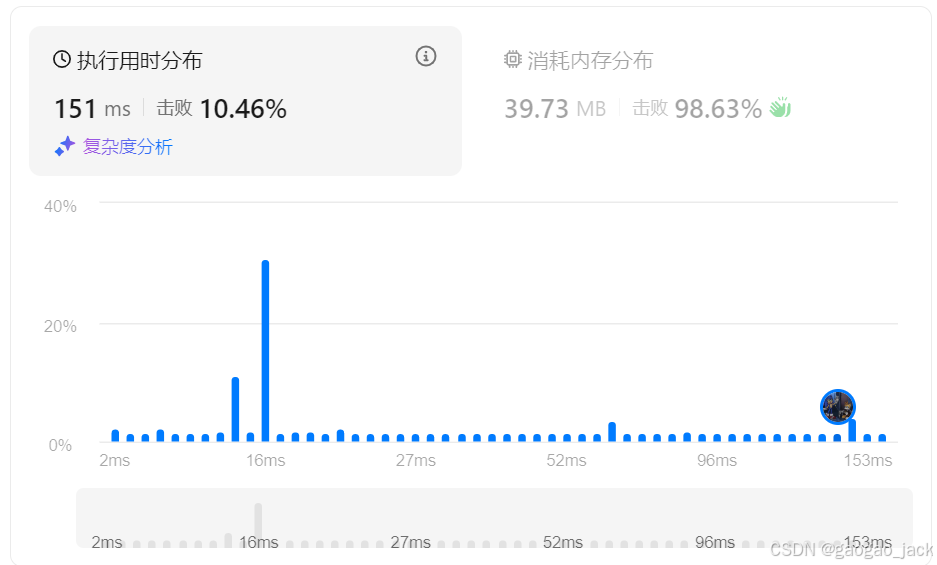
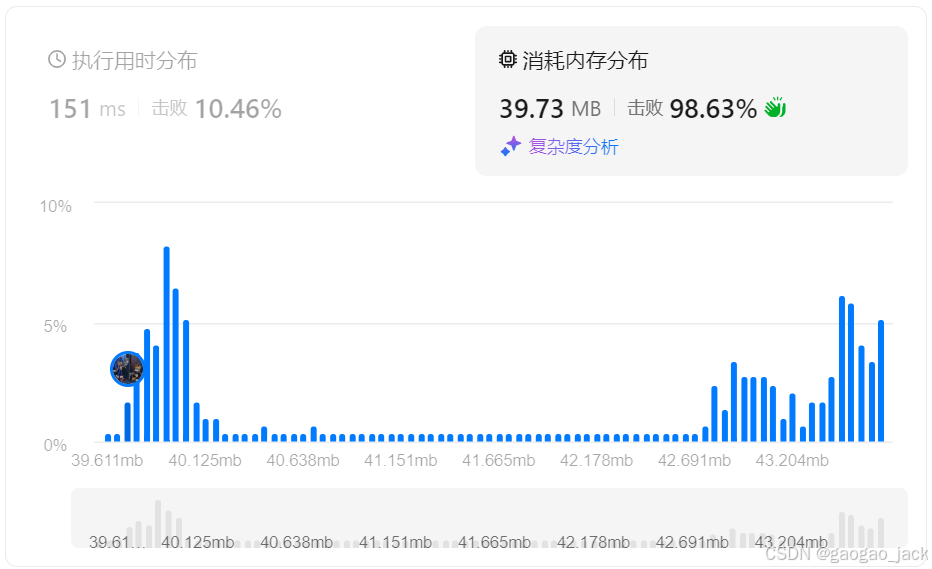
方法二：埃拉托斯特尼筛法(埃氏筛)

参考链接：https://leetcode.cn/problems/find-the-count-of-numbers-which-are-not-special/solutions/2860320/3233-tong-ji-bu-shi-te-shu-shu-zi-de-shu-enhg/

原理：“埃拉托斯特尼筛法，简称埃氏筛，是由希腊数学家埃拉托斯特尼提出的筛选质数的算法。埃氏筛的原理是：对于质数 p，所有大于 p 的 p 的倍数都是合数，根据该性质移除所有的合数。

使用埃氏筛得到不超过 upperBound 的所有质数的做法是：使用列表记录从 2 到 upperBound 的所有整数，每次保留列表中的最小整数 p，将 p 保留，并将列表中的所有大于 p 的 p 的倍数都删除，当没有更多的整数可以删除时，剩下的数就是不超过 upperBound 的所有质数。”

class Solution {public int nonSpecialCount(int l, int r) {int lowerBound = (int) Math.ceil(Math.sqrt(l));//下界int upperBound = (int) Math.floor(Math.sqrt(r));//上界boolean[] isPrime = new boolean[upperBound + 1];Arrays.fill(isPrime, true);isPrime[0] = false;isPrime[1] = false;for(int i = 2; i * i <= upperBound; i++) {if(isPrime[i]) {for(int j = i * i; j <= upperBound; j += i) isPrime[j] = false;}}int res = 0;for(int i = lowerBound; i <= upperBound; i++) {if(isPrime[i]) res++;}return r-l+1-res;//总数减去是特殊数字的数量即为不是特殊数字的数量}
}

时间复杂度： $O(\sqrt{r}\log \log\sqrt{r})$ ，其中 r 是给定的区间上界。

空间复杂度： $O(\sqrt{r})$ ，其中 r 是给定的区间上界。

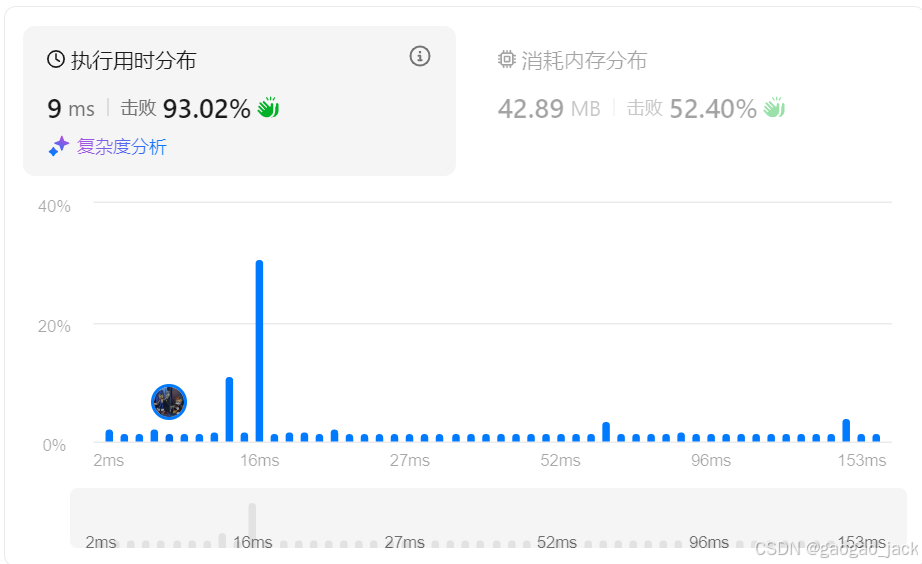
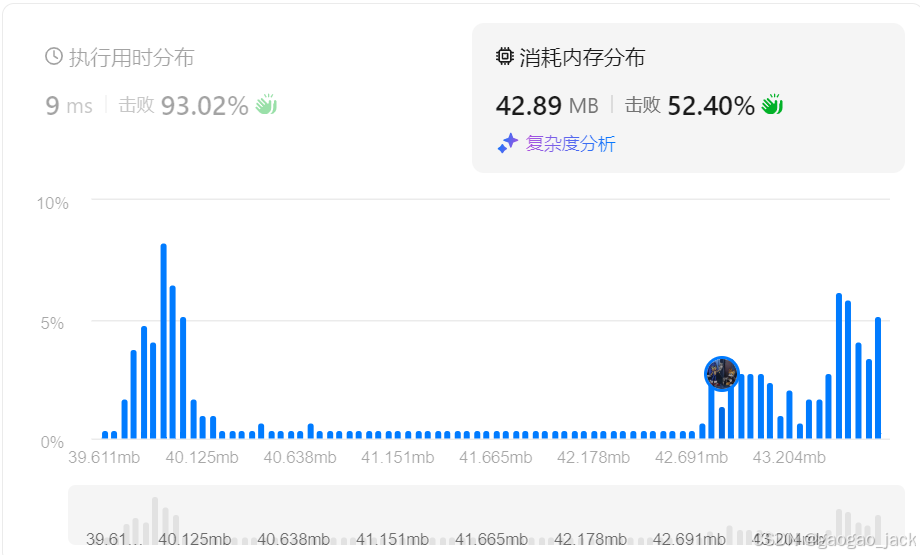
方法三：欧拉筛(线性筛)->避免重复标记

参考链接：https://leetcode.cn/problems/find-the-count-of-numbers-which-are-not-special/solutions/2860320/3233-tong-ji-bu-shi-te-shu-shu-zi-de-shu-enhg/

该方法可看作是方法二的改进版，因为埃氏筛存在重复标记的情况，如果一个合数有多个不同的质因数，则会被标记多次，比如30会被2、3、5分别标记一次。

原理(引用自参考链接)：

class Solution {public int nonSpecialCount(int l, int r) {int lb = (int) Math.ceil(Math.sqrt(l));//下界int ub = (int) Math.floor(Math.sqrt(r));//上界List<Integer> primes = new ArrayList<Integer>();boolean[] isPrime = new boolean[ub+1];Arrays.fill(isPrime, true);isPrime[0] = false;isPrime[1] = false;for(int i=2;i<=ub;i++) {if(isPrime[i]) primes.add(i);for(int prime:primes) {if(i*prime<=ub) {isPrime[i*prime]=false;if(i%prime==0) break;}else break;}}int res=0;for(int i=lb;i<=ub;i++){if(isPrime[i]) res++;//是特殊数字的数字数量}return r-l+1-res;//总数-是特殊数字的数字数量即为题目答案}
}

时间复杂度： $O(\sqrt{r})$ ，其中 r 是给定的区间上界。

空间复杂度： $O(\sqrt{r})$ ，其中 r 是给定的区间上界。

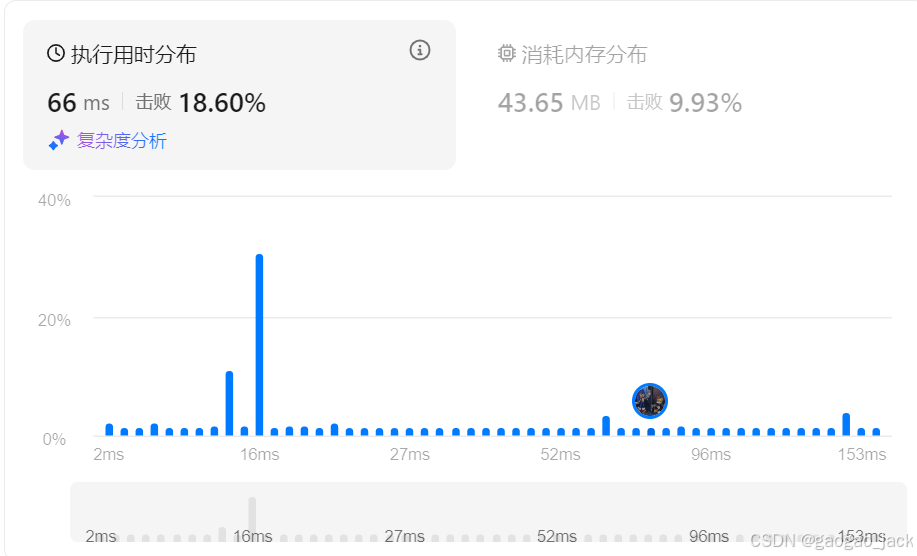
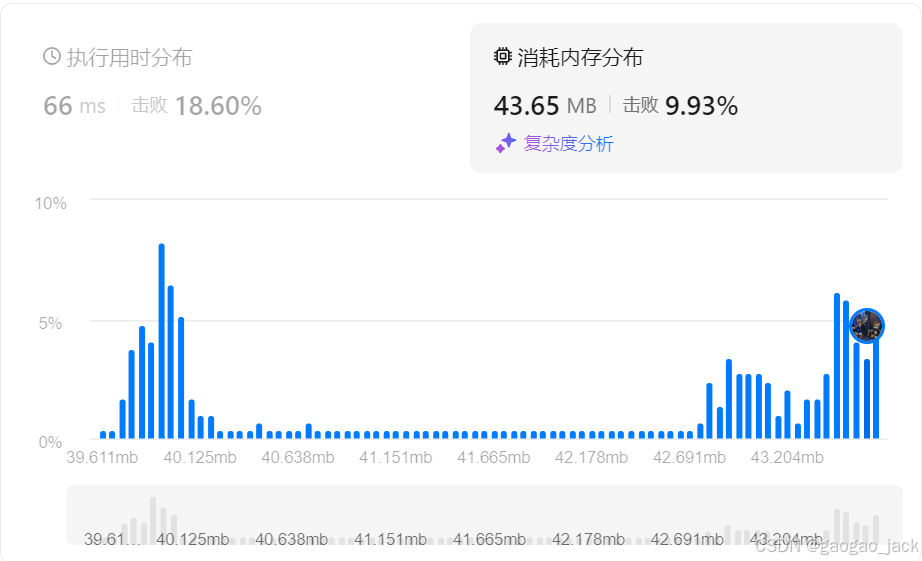
方法四：求范围内质数

参考链接：https://leetcode.cn/problems/find-the-count-of-numbers-which-are-not-special/solutions/2887918/3233-tong-ji-bu-shi-te-shu-shu-zi-de-shu-zxa2/

该方法可看作是方法一的优化。
思路：首先根据题意，特殊数字是指除1和本身外只包含一个质数的数字。即相当于质数的平方。然后对数据进行预处理，判断范围内的质数。对于质数范围，假设右边界r是特殊数字，则必然存在一个质数Math.sqrt(r)，即为质数范围最大值。然后完成问题转换，将[l,r]区间单个进行枚举判断，转为根据范围内质数算出特殊数字，并判断是否落在区间内。最后用总数减去特殊数字个数即为题目结果。

class Solution {public int nonSpecialCount(int l, int r) {int n = (int) Math.sqrt(r) + 1;boolean[] pir = getPrimeInRange(n);// 统计特殊数字个数int res=0;for (int i = 0; i < pir.length ;i++) {if (!pir[i]) continue;// 当前i为质数，num为特殊数字int num=i*i;// 判断特殊数字是否落在lr区间内if (num > r) break;else if (num < l) continue;else res++;}return r-l+1-res;}private static boolean[] getPrimeInRange(int n) {// 函数作用：判断范围内的质数boolean[] isPrime = new boolean[n];// 使用数组存储该位是否为质数Arrays.fill(isPrime, true);isPrime[1] = false;for(int i=2;i*i<n;i++) {if(isPrime[i]) {for (int j = i * i; j < n; j += i) isPrime[j] = false; // 原数是质数，在范围n内累乘迭代，结果均为非质数}}return isPrime;}
}

时间复杂度： $O(n\log n)$

空间复杂度： $O(n)$

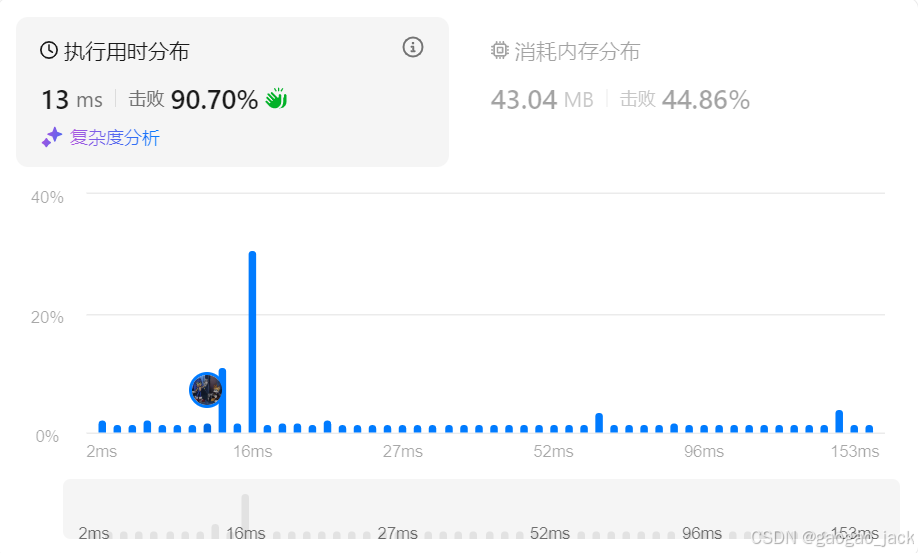
方法五：预处理质数(灵神解法)

(该方法较为巧妙)

参考链接：https://leetcode.cn/problems/find-the-count-of-numbers-which-are-not-special/solutions/2860276/yu-chu-li-zhi-shu-o1hui-da-pythonjavacgo-7xaq/

class Solution {private static final int Max = 31622;private static final int[] p = new int[Max + 1];static{for (int i = 2; i <= Max; i++) {if (p[i] == 0){// i 是质数p[i] = p[i-1] + 1;for (int j = i * i; j <=Max; j += i) p[j] = -1; // 标记 i 的倍数为合数 // 注：如果 MX 比较大，小心 i*i 溢出} else p[i] = p[i - 1];}}public int nonSpecialCount(int l, int r) {return r-l+1-(p[(int)Math.sqrt(r)]-p[(int)Math.sqrt(l-1)]);}
}

时间复杂度： $O(1)$ ，预处理不计。