- 训练深层神经网络是十分困难的,特别是在较短的时间内使它们收敛更加棘手。而本节的批量规范化(batch normalization) 可以持续加速深层网络的收敛速度
- 结合下节会介绍道德残差块,批量规范化使得研究人员能够训练100层以上的网络
1. 训练深层网络
- 为什么要批量规范化层呢?下面回顾一下训练神经网络时出现的实际挑战
- 首先,数据的预处理方式通常会对最终结果产生巨大影响。在前面我们预测房价实战中,我们第一步是标准化输入特征,使其均值为 0,方差为 1。这种标准化可以很好地配合我们的优化器,因为它可以将参数的量级进行同一
- 对于 MLP 或 CNN。当我们训练时,中间层的变量可能有更广的变化范围:无论是沿着从输入到输出的层,跨同一层中的单元,或是随着时间的推移,模型参数随着训练更新变幻莫测
- 批量规范化的发明者非正式地假设,这些变量分布中的这种偏移可能会阻碍网络收敛。如果一个层的可变值是另一个层的100倍,这可能需要学习率进行补偿
- 更深层的网络很复杂,容易过拟合,这意味着正则化变得更加重要
- 批量规范化可以应用于单个可选层,也可以应用到所有层。原理如下:在每次训练迭代中,我们首先规范化输入,即通过减去均值并除以标准差,其中两者均基于当前小批量处理。接下来我们应用比例系数和比例偏移。由于是基于批量统计的标准化,所以i叫批量规范化
- 如果我们尝试使用大小为1的小批量应用批量规范化,我们将无法学到任何东西。这是因为在减去均值之后,每个隐藏单元将为0。 所以,只有使用足够大的小批量,批量规范化这种方法才是有效且稳定的。 请注意,在应用批量规范化时,批量大小的选择可能比没有批量规范化时更重要。

- 在训练过程中,中间层的变化幅度不能过于剧烈,而批量规范化将每一层主动居中,并将它们重新调整为给定的平均值和大小

- 由于某些尚未被明确的原因,优化中各种噪声源通常会导致更快的训练和较少的过拟合,这种变化似乎是正则化的一种形式
- 另外,批量规范化层在”训练模式“(通过小批量统计数据规范化)和“预测模式”(通过数据集统计规范化)中的功能不同。 在训练过程中,我们无法得知使用整个数据集来估计平均值和方差,所以只能根据每个小批次的平均值和方差不断训练模型。 而在预测模式下,可以根据整个数据集精确计算批量规范化所需的平均值和方差。
- 下面来看是如何在实践中工作的
2. 批量规范化层
- 回想一下,批量规范化和其他层之间的一个关键区别是批量规范化在完整的小批量上运行,因此我们不能像以前在引入其他层时那样忽略批量大小。
- 我们在下面讨论这两种情况:全连接层和卷积层,他们的批量规范化实现略有不同。
2.1 全连接层

2.2 卷积层
- 对于卷积层,可以在卷积层之后和非线性激活函数之前进行批量规范化,每个通道都有自己的拉伸和偏移参数,两个参数都是标量
- 假设我们的小批量包含 m 个样本,并且对于每个通道,卷积的输出具有高度 p和宽度 q。 那么对于卷积层,我们在每个输出通道的 mpq 个元素上同时执行每个批量规范化。 因此,在计算平均值和方差时,我们会收集所有空间位置的值,然后在给定通道内应用相同的均值和方差,以便在每个空间位置对值进行规范化。
2.3 预测过程中的批量规范化
- 批量规范化在训练模式和预测模式下的行为通常不同
- 将训练好的模型用于预测时,我们不再需要样本均值中的噪声以及在微批次上估计每个小批次产生的样本方差了
- 我们可能需要使用我们的模型对逐个样本进行预测。 一种常用的方法是通过移动平均估算整个训练数据集的样本均值和方差,并在预测时使用它们得到确定的输出
- 和暂退法一样,批量规范化层在训练模式和预测模式下的计算结果也是不一样的
3. 从零开始实现
- 下面是实现代码



- 我们现在可以创建一个正确的BatchNorm层。 这个层将保持适当的参数:拉伸gamma和偏移beta,这两个参数将在训练过程中更新
- 我们的层将保存均值和方差的移动平均值,以便在模型预测期间随后使用

4. 使用批量规范化层的LeNet
- 为了更好地理解BatchNorm,下面我们将其应用于LeNet模型。批量规范化是在卷积层或全连接层之后、相应的激活函数之前应用的。

- 我们再在Fashion-MNIST数据集上训练网络,但不同的是学习率大得多,下面的补充内容会提到为什么可以上更大的学习率

5. 简明实现
- 我们可以直接使用深度学习框架中定义的BatchNorm。 代码看起来几乎与我们上面的代码相同。

6. 补充
- 下面是我在b站上看的一个视频的笔记,看了之后感觉清晰了很多:https://www.bilibili.com/video/BV12d4y1f74C/?spm_id_from=333.880.my_history.page.click&vd_source=bab99a4bc7d540abf82733d55fa02cca
- 在网络学习的过程中,全一层的输出就是后一层的输入,因此由于参数的更新,每层的输入分布都在发生变化,这会导致网络很难收敛

- 而为了能够收敛,那么就需要:① 学习率不能太高。 ② 参数初始化准确。 ③ 网络层数不能太多。
- 而神经网络的研究人员发现,这个现象是由于每层分布的差异过大,且无法预测而导致的。那么如果让每一个batch在每一层中都服从类似的分布,就可以解决这一的问题了

- 加上伽马和贝塔是因为我们不想每层输入的分布都相同

- 在加上了Batch Normalization,那么我们就可以:① 使用较大的学习率。 ② 参数初始化不敏感。 ③ 加快网络训练。
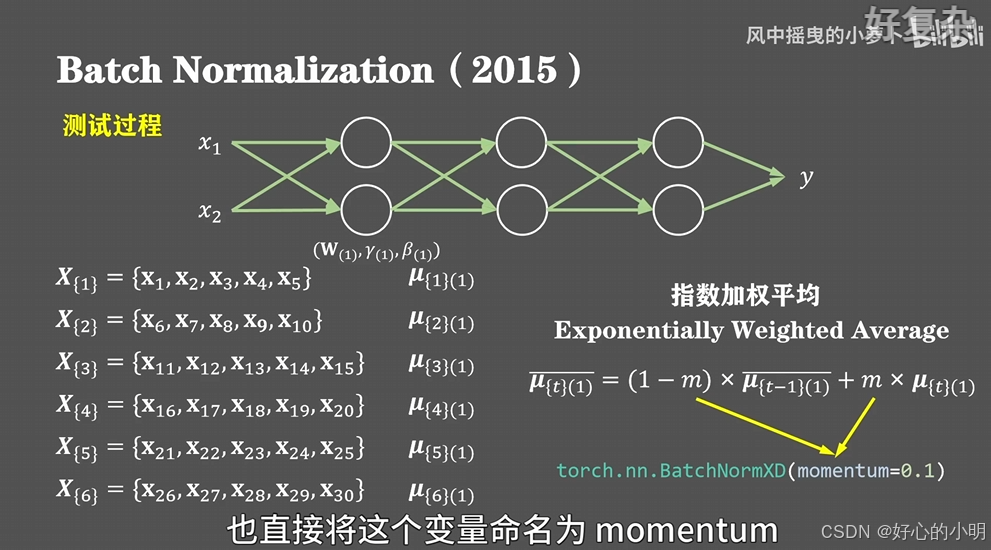
- 在测试推理阶段,我们仍然可以使用训练得到的伽马和贝塔两个参数。但是训练集和测试集的样本分布不完全一致,并且我们可能只使用一个样本进行测试,无法计算均值和标准差。因此我们需要保存并使用训练过程中的结果来辅助运算
- 假设我们有30个样本,每五个样本构成一个batch进行训练,完整遍历一次训练集就需要六个batch,那么对于第一层神经网络来说我们会得到六个均值的历史数值,那么接下来通过指数加权,获得这六个均值的平均值,下面的m可以看作是对历史的保留,非常类似于随机梯度下降中动量的概念,在torch框架中也直接将这个变量命名为 momentum,默认值为0.1
- Batch Normalization可以加速神经网络收敛。但是①仅在样本数量较多时有效。② 对RNN或序列数据性能较差。 ③ 分布式运算时影响效率















)



