10. 灾后重建
Pear市一共有N(<=50000)个居民点,居民点之间有M(<=200000)条双向道路相连。这些居民点两两之间都可以通过双向道路到达。这种情况一直持续到最近,一次严重的地震毁坏了全部M条道路。
震后,Pear打算修复其中一些道路,修理第i条道路需要Pi的时间。不过,Pear并不打算让全部的点连通,而是选择一些标号特殊的点让他们连通。
Pear有Q(<=50000)次询问,每次询问,他会选择所有编号在[l,r]之间,并且 编号 mod K = C 的点,修理一些路使得它们连通。由于所有道路的修理可以同时开工,所以完成修理的时间取决于花费时间最长的一条路,即涉及到的道路中Pi的最大值。你能帮助Pear计算出每次询问时需要花费的最少时间么?这里询问是独立的,也就是上一个询问里的修理计划并没有付诸行动。
【输入格式】
第一行三个正整数N、M、Q,含义如题面所述。
接下来M行,每行三个正整数Xi、Yi、Pi,表示一条连接Xi和Yi的双向道路,修复需要Pi的时间。可能有自环,可能有重边。1<=Pi<=1000000。
接下来Q行,每行四个正整数Li、Ri、Ki、Ci,表示这次询问的点是[Li,Ri]区间中所有编号Mod Ki=Ci的点。保证参与询问的点至少有两个。【输出格式】
输出Q行,每行一个正整数表示对应询问的答案。【样例输入】
7 10 4
1 3 10
2 6 9
4 1 5
3 7 4
3 6 9
1 5 8
2 7 4
3 2 10
1 7 6
7 6 9
1 7 1 0
1 7 3 1
2 5 1 0
3 7 2 1【样例输出】
9
6
8
8【数据范围】
对于20%的数据,N,M,Q<=30
对于40%的数据,N,M,Q<=2000
对于100%的数据,N<=50000,M<=2*10^5,Q<=50000. Pi<=10^6.
Li,Ri,Ki均在[1,N]范围内,Ci在[0,对应询问的Ki)范围内。资源约定:
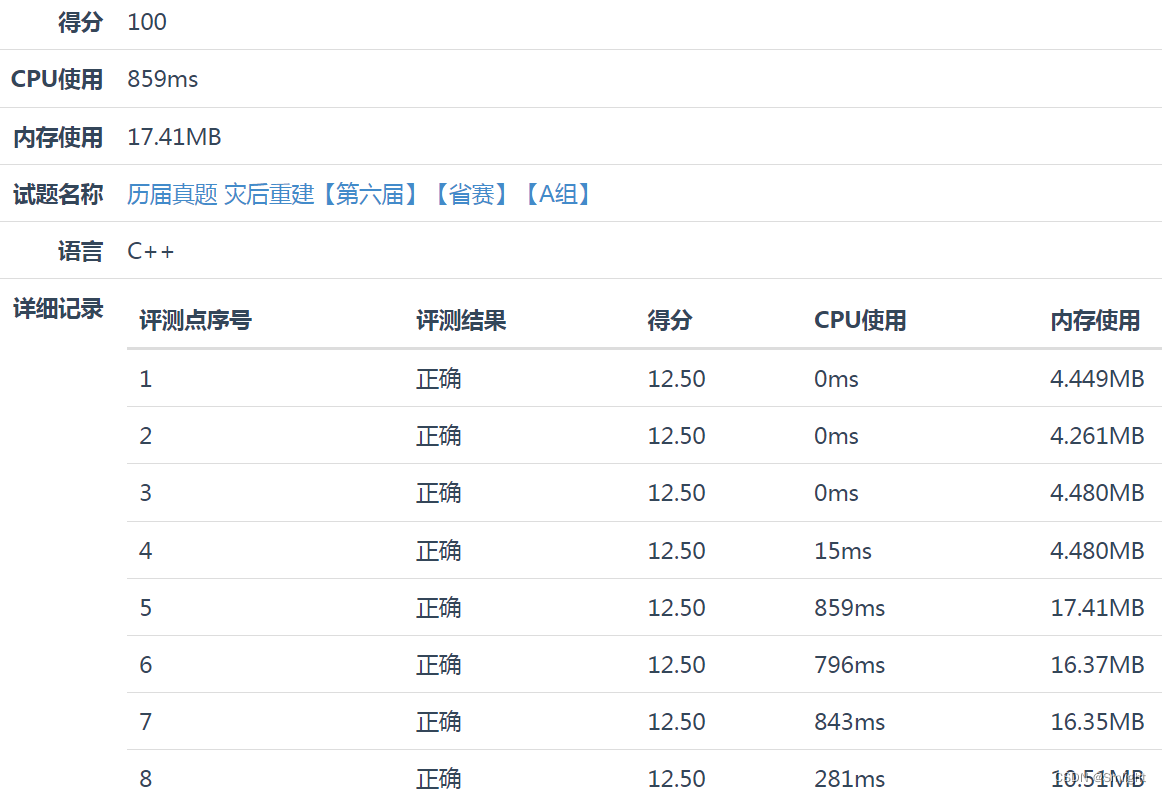
峰值内存消耗 < 256M
CPU消耗 < 5000ms请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include , 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
这题比较复杂,算法总共要分为三个部分。
首先,每次询问其实都是给出一个特定点集,要求最小化把这些点连通的边权的最大值。
那么,该问题是MST问题的变体 最小生成树资料
进一步地,对于每次询问,最佳方案的边都在原图的最小生成树中,可由反证法证得。
因此,算法的第一部分就是抛弃原图,只留下最小生成树,边数减少到 n − 1 n-1 n−1,并且有很多好用的特征。
任选一点使之成为有根树,树上任意两点有且仅有一条简单路径,也即两点分别向上连到LCA 最近公共祖先资料
本题所取点集与除法取模有关,可以考虑 Big Small 分界。参考资料:fold的毒瘤题
设定一个阈值 T T T,
- 当 k > T k>T k>T时,点数约为 n k \frac{n}{k} kn,至多为 n T \frac{n}{T} Tn,顺序遍历所有点是可接受的。
可以对LCA分类讨论证得,点1点3路径的最大值,其实已包含在点1点2路径和点2点3路径。
因此,对于特定点集并不需要两两求LCA,只需要对“相邻”点顺序求过去就行。
由于原图的MST不会变动,可以采用倍增预处理的方法作为算法的第二部分。 - 当 k < = T k<=T k<=T时, k k k的取值至多有 T T T种,遍历不同的 k k k是可接受的。
考虑到上述“相邻”的特性,其实对于同一组 ( k , c ) (k,c) (k,c),就是多次查询不同的 ( l , r ) (l,r) (l,r)区间,
因为本题允许离线处理,可以把所有符合条件的点的路径建立数据结构,这是算法的第三部分。
同样是没有修改,这里用线段树来优化查询速度 线段树资料
当 T T T取 n \sqrt n n时,总体复杂度最小。
进一步分析发现,该方法还可以简化,下面说明只用线段树方法复杂度仍然是正确的。
考虑最极端情况,每次询问的 ( k , c ) (k,c) (k,c)均不同,每次都需要重新建树,因为 k k k越小点集越大,且对于每个 k k k, c c c各有 k k k种取值,因此求LCA和建树的总复杂度为
T ( n ) = n 1 ( log n + log n 1 ) + ( n 2 ( log n + log n 2 ) ) × 2 + ( n 3 ( log n + log n 3 ) ) × 3 + … T(n) = \frac{n}{1}(\log n + \log \frac{n}{1}) + (\frac{n}{2}(\log n + \log \frac{n}{2})) \times 2 + (\frac{n}{3}(\log n + \log \frac{n}{3})) \times 3 + \dots T(n)=1n(logn+log1n)+(2n(logn+log2n))×2+(3n(logn+log3n))×3+…
≤ n ⋅ 2 log n + n ⋅ 2 log n + n ⋅ 2 log n + … \le n \cdot 2 \log n + n \cdot 2 \log n + n \cdot 2 \log n + \dots ≤n⋅2logn+n⋅2logn+n⋅2logn+…
= O ( n ⋅ n ⋅ log n ) = O(\sqrt{n} \cdot n \cdot \log n) =O(n⋅n⋅logn)
查询的总复杂度显然是 O ( q ⋅ log n ) O(q \cdot \log n) O(q⋅logn),两部分都完全没毛病。
本题从 Big Small 分界出发,到最后发现其实并不需要 Big Small 分界,直接建简化线段树的复杂度也是没有问题的,真是挺有趣的。
不过在线练习系统只给了1s的时限就比较紧,这就必须得套个读入优化才能保证每次都过了,读入量接近百万级(20w*3+5w*4)。
#include <bits/stdc++.h>
using namespace std;typedef pair<int, int> PII;
const int N = 50010;
const int M = 200010;
const int FN = 16;
vector<PII> G[N];
int dep[N], ans[N];
int fa[N][FN], val[N][FN];
struct Que {int x, l, r, k, c;
} que[N];
bool debug = false;inline void getmax(int& x, int y)
{if (y > x)x = y;
}namespace Kruskal {
int p[N], ra[N];
struct Edge {int u, v, w;
} eg[M];int cmp(const Edge& p1, const Edge& p2) { return p1.w < p2.w; }int find(int x) { return p[x] == x ? x : p[x] = find(p[x]); }int merge(int x, int y)
{x = find(x);y = find(y);if (x == y)return 0;if (ra[x] > ra[y]) {p[y] = x;} else {if (ra[x] == ra[y])ra[y]++;p[x] = y;}return 1;
}void build(int kn, int km)
{int cnt = 0;for (int i = 1; i <= kn; i++) {p[i] = i;ra[i] = 0;}sort(eg + 1, eg + km + 1, cmp);for (int i = 1; i <= km; i++) {if (merge(eg[i].u, eg[i].v)) {G[eg[i].u].push_back(PII(eg[i].v, eg[i].w));G[eg[i].v].push_back(PII(eg[i].u, eg[i].w));if (++cnt == kn - 1)break;}}
}
} // namespace Kruskalclass SegTree {
#define lson rt << 1, l, m
#define rson rt << 1 | 1, m + 1, r
public:int key[N << 2];void build(int a[], int rt, int l, int r){if (l == r) {key[rt] = a[l];return;}int m = (l + r) >> 1;build(a, lson);build(a, rson);push_up(rt);}int query(int rt, int l, int r, int L, int R){if (L <= l && r <= R) {return key[rt];}int m = (l + r) >> 1;int res = 0;if (L <= m)getmax(res, query(lson, L, R));if (m < R)getmax(res, query(rson, L, R));return res;}private:inline void push_up(int rt){key[rt] = max(key[rt << 1], key[rt << 1 | 1]);}
#undef lson
#undef rson
};
SegTree T;void dfs(int u, int x)
{for (size_t i = 0; i < G[u].size(); i++) {int v = G[u][i].first;int w = G[u][i].second;if (v != x) {dep[v] = dep[u] + 1;fa[v][0] = u;val[v][0] = w;dfs(v, u);}}
}bool cmpkc(const Que& p, const Que& q)
{return p.k < q.k || (p.k == q.k && p.c < q.c);
}int query(int x, int y)
{if (x == 0)return 0;if (dep[x] > dep[y])swap(x, y);int res = 0, di = dep[y] - dep[x];for (int k = 0; k < FN; k++) {if ((di >> k) & 1) {getmax(res, val[y][k]);y = fa[y][k];}}int k = FN - 1;while (x != y) {while (k > 0 && fa[x][k] == fa[y][k])--k;getmax(res, val[x][k]);getmax(res, val[y][k]);x = fa[x][k];y = fa[y][k];}return res;
}template <class T>
inline bool read(T& x)
{char c;int neg = 0;if (c = getchar(), c == EOF)return false; // EOFwhile (c != '-' && (c < '0' || c > '9'))c = getchar();if (c == '-')neg = 1, c = getchar();x = (c - '0');while (c = getchar(), c >= '0' && c <= '9')x = (x << 3) + (x << 1) + (c - '0');if (neg)x = -x;return true;
}int main()
{int n, m, q;read(n);read(m);read(q);{using namespace Kruskal;for (int i = 1; i <= m; i++) {read(eg[i].u);read(eg[i].v);read(eg[i].w);}build(n, m);} // now G is MSTfa[1][0] = 1;dep[1] = 1;dfs(1, 0);for (int k = 1; k < FN; k++) {for (int i = 1; i <= n; i++) {fa[i][k] = fa[fa[i][k - 1]][k - 1];val[i][k] = max(val[i][k - 1], val[fa[i][k - 1]][k - 1]);}}for (int i = 1; i <= q; i++) {read(que[i].l);read(que[i].r);read(que[i].k);read(que[i].c);que[i].x = i;}sort(que + 1, que + q + 1, cmpkc);int tmp[N], tlen;for (int x = 1; x <= q; x++) {int k = que[x].k, c = que[x].c;if (k != que[x - 1].k || c != que[x - 1].c) {// not same, rebuild segtreetlen = 0;for (int i = c; i + k <= n; i += k) {tmp[++tlen] = query(i, i + k);}T.build(tmp, 1, 1, tlen);}ans[que[x].x] = T.query(1, 1, tlen, (que[x].l - c + k - 1) / k + 1, (que[x].r - c) / k);}for (int i = 1; i <= q; i++) {printf("%d\n", ans[i]);}return 0;
}






)
)



方法源码分析)


事务管理)




