目录

简介

第一个错误的版本

算法思路

代码实现

两个数组的交集

算法思路

代码实现

两个数组的交集2

算法思路

代码实现

有效的完全平方数

算法思路

代码实现

猜数字大小

算法思路

代码实现

排列硬币

算法思路

代码实现

寻找比目标字母大的最小字母

代码实现

总结

---

简介

前面已经学过了二分算法,时间久了就会忘记,所以应该抽出时间进行复习,下面是我leetcode中写的几道简单的二分题来唤醒死去的记忆.想复习懒得手写的小伙伴可以来看看哦;

第一个错误的版本

地址:. - 力扣（LeetCode）

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例 1：

输入：n = 5, bad = 4
输出：4
解释：
调用 isBadVersion(3) -> false 
调用 isBadVersion(5) -> true 
调用 isBadVersion(4) -> true
所以，4 是第一个错误的版本。

示例 2：

输入：n = 1, bad = 1
输出：1

算法思路

这道题给的序列是递增的, 我们根据题意可以区分出二段性将数组分成两部分,左边都是好的版本右边都是坏的版本.让我们找出第一坏的版本.
首先最后循环结束时,mid肯定是落在正确结果上的,也就是指向的是第一个坏的版本,是不可能越过右边部分的.我们把mid当成最后的结果,那么就是始终是不可能是mid-1的所以在二分时left=mid+1,right=mid;这个时候需要注意的是求mid时得是left+(right-left)/;如果是left+(right-left+1)/2可能会发生死循环;如此一来便可解之;

关键点在于right和mid是在同一侧(根据二段性将数组分为了两个部分)的,所以right就不可能会越过mid;然后再检查下mid的方式;

代码实现

// The API isBadVersion is defined for you.
// bool isBadVersion(int version);class Solution {
public:int firstBadVersion(int n) {int left=1;int right=n;while(left<right){int mid=left+(right-left)/2;if(isBadVersion(mid)==true)right=mid;else left=mid+1;}return right;}
};

两个数组的交集

地址:. - 力扣（LeetCode）

给定两个数组 nums1 和 nums2 ，返回 它们的 

交集

 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

示例 2：

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
解释：[4,9] 也是可通过的

算法思路

这道题标签是二分,但是本人并没有看出来怎么二分,因为每个元素都是唯一的,所以直接使用set进行去重,然后以一个数组为基准,遍历另外一个数组;

代码实现

class Solution {
public:bool isPerfectSquare(int num) {if(num==1)return true;int left=1;int right=num;while(left<right){long long mid=left+(right-left)/2;if(mid*mid>num)right=mid;else if(mid*mid<num)left=mid+1;else return true;}return false ;}
};

两个数组的交集2

地址:. - 力扣（LeetCode）

给你两个整数数组 nums1 和 nums2 ，请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数，应与元素在两个数组中都出现的次数一致（如果出现次数不一致，则考虑取较小值）。可以不考虑输出结果的顺序。

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2,2]

示例 2:

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[4,9]

算法思路

与1不同的是,这个数组中的元素并不是唯一的,我们可以使用哈希表来进行去重,转化为类似于1的形式,以一个数组为标准,遍历另外一个数组,额外多出的一点就是需要判断两个数组中重复元素的个数,小的那个才是结果;

代码实现

class Solution {
public:vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {int hash1[1001];int hash2[1001];for(auto &x:nums1)hash1[x]++;for(auto &x:nums2)hash2[x]++;vector<int>ret;set<int>s(nums2.begin(),nums2.end());//进行去重for(auto &x:s){if(hash1[x]){int a=hash1[x];int b=hash2[x];//插入数量小的int n=min(a,b);for(int i=0;i<n;i++)ret.push_back(x);}}return ret;}
};

有效的完全平方数

地址:. - 力扣（LeetCode）

给你一个正整数 num 。如果 num 是一个完全平方数，则返回 true ，否则返回 false 。

完全平方数 是一个可以写成某个整数的平方的整数。换句话说，它可以写成某个整数和自身的乘积。

不能使用任何内置的库函数，如  sqrt 。

示例 1：

输入：num = 16
输出：true
解释：返回 true ，因为 4 * 4 = 16 且 4 是一个整数。

示例 2：

输入：num = 14
输出：false
解释：返回 false ，因为 3.742 * 3.742 = 14 但 3.742 不是一个整数。

算法思路

这道题就是在1道-num之间的数中找到一个数的平方等于num,根据结果来说我们可以将mid*mid大于等于num的分为右边,mid*mid小于num的分为左边,我们只需要求出第一个大于等于部分的数即可(right和mid在同一侧);所以二分过程中left=mid+1,right=mid;  mid=left+(right-left)/2;

代码实现

class Solution {
public:bool isPerfectSquare(int num) {if(num==1)return true;int left=1;int right=num;while(left<right){long long mid=left+(right-left)/2;if(mid*mid>num)right=mid;else if(mid*mid<num)left=mid+1;else return true;}return false ;}
};

猜数字大小

地址:. - 力扣（LeetCode）

我们正在玩猜数字游戏。猜数字游戏的规则如下：

我会从 1 到 n 随机选择一个数字。 请你猜选出的是哪个数字。

如果你猜错了，我会告诉你，我选出的数字比你猜测的数字大了还是小了。

你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果，返回值一共有三种可能的情况：

• -1：你猜的数字比我选出的数字大 （即 num > pick）。
• 1：你猜的数字比我选出的数字小 （即 num < pick）。
• 0：你猜的数字与我选出的数字相等。（即 num == pick）。

返回我选出的数字。

示例 1：

输入：n = 10, pick = 6
输出：6

示例 2：

输入：n = 1, pick = 1
输出：1

算法思路

与检查版本的一样,无需多言.

代码实现

class Solution {
public:int guessNumber(int n) {int left=1;int right=n;while(left<right){long long  mid=left+(right-left)/2;if(guess(mid)<0)right=mid;else if(guess(mid)>0)left=mid+1;else return mid;}return right;}
};

排列硬币

地址:. - 力扣（LeetCode）

你总共有 n 枚硬币，并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯，其第 i 行必须正好有 i 枚硬币。阶梯的最后一行 可能 是不完整的。

给你一个数字 n ，计算并返回可形成 完整阶梯行 的总行数。

示例 1：

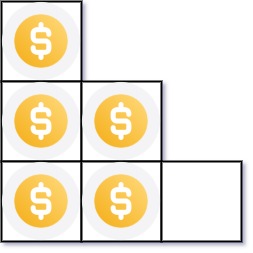
输入：n = 5
输出：2
解释：因为第三行不完整，所以返回 2 。

示例 2：

输入：n = 8
输出：3
解释：因为第四行不完整，所以返回 3 。

算法思路

这道题就是硬币数和结题书进行比较,老玩法了,无需多言.

代码实现

class Solution {
public:int arrangeCoins(int n) {int left=1;int right=n;while(left<right){long long mid=left+(right-left+1)/2;long long  ret=(1+mid)*mid/2;if(ret<=n)left=mid;else right=mid-1;}return right;}
};

寻找比目标字母大的最小字母

地址:. - 力扣（LeetCode）

给你一个字符数组 letters，该数组按非递减顺序排序，以及一个字符 target。letters 里至少有两个不同的字符。

返回 letters 中大于 target 的最小的字符。如果不存在这样的字符，则返回 letters 的第一个字符。

示例 1：

输入: letters = ["c", "f", "j"]，target = "a"
输出: "c"
解释：letters 中字典上比 'a' 大的最小字符是 'c'。

示例 2:

输入: letters = ["c","f","j"], target = "c"
输出: "f"
解释：letters 中字典顺序上大于 'c' 的最小字符是 'f'。

示例 3:

输入: letters = ["x","x","y","y"], target = "z"
输出: "x"
解释：letters 中没有一个字符在字典上大于 'z'，所以我们返回 letters[0]。

代码实现

class Solution {
public:char nextGreatestLetter(vector<char>& letters, char target) {int left=0;int right=letters.size()-1;while(left<right){int mid=left+(right-left)/2;if(letters[mid]>target)right=mid;else left=mid+1;}if(letters[right]<=target)return letters[0];return letters[right];}
};

总结

1.确定边界left和right;
2.区分二段性,判断最终的mid和left同侧还是跟right同侧;
3.如果是mid和left同侧,那么left=mid;right=mid-1;mid=left+(right-left+1)/2;反之,right=mid;left=mid+1;mid=left+(right-left)/2;