2024年了,PINN网络依然火爆,各大顶会顶刊都能看见它的相关论文。
这是因为,AI交叉学科通常离不开求解偏微分方程PDE,而传统的求解方法受初始假设限制,一旦没设好就会导致很大的误差。
PINN作为一种新的思路,但凡涉及到求解PDE,理论上都可以适用,它可以处理复杂几何和边界条件,无需网格就可以计算,实现快速求解PDE,满足我们解决实际复杂问题建模后求解需求,因此在各个领域中都有用武之地。
目前有关PINN求解PDE的创新主要围绕网络结构优化、正则化方法、损失函数构造等。为了方便想发论文的同学,我根据这些创新方向整理了9篇最新的PINN求解PDE论文,开源的代码已附。
论文原文+开源代码需要的同学看文末
Gpt-pinn: Generative pre-trained physics-informed neural networks toward non-intrusive meta-learning of parametric pdes
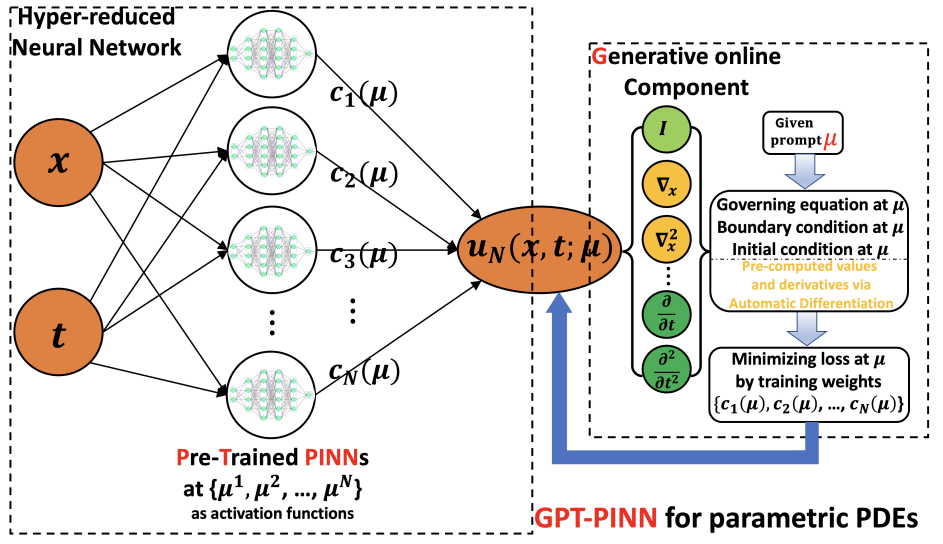
方法:论文提出了一种新型的物理信息神经网络框架,称为生成预训练的PINN(GPT-PINN),它用于求解参数化的偏微分方程(PDEs)。GPT-PINN的核心思想是结合元学习(meta-learning)和深度学习技术,以提高求解参数化PDEs的效率和准确性。
创新点:
-
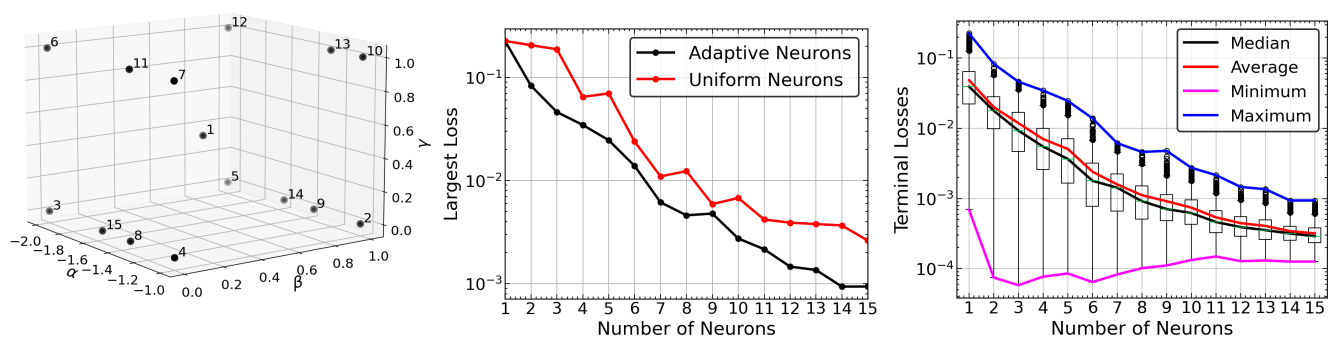
设计了具有定制激活函数的网络架构,这些激活函数是通过贪婪算法选择的参数值实例化的预训练PINNs。这是首次将整个(预训练)网络用作一个神经元的激活函数。
-
提出了一种全新的元学习范式,即GPT-PINN,用于解决参数化系统中PINNs面临的训练成本和过度参数化的挑战。
-
借鉴了经典的RBM技术,采用策略来显著减小PINNs的规模,并加速使用PINNs求解参数化PDE的过程。
Physics-Informed Neural Operator for Learning Partial Differential Equations
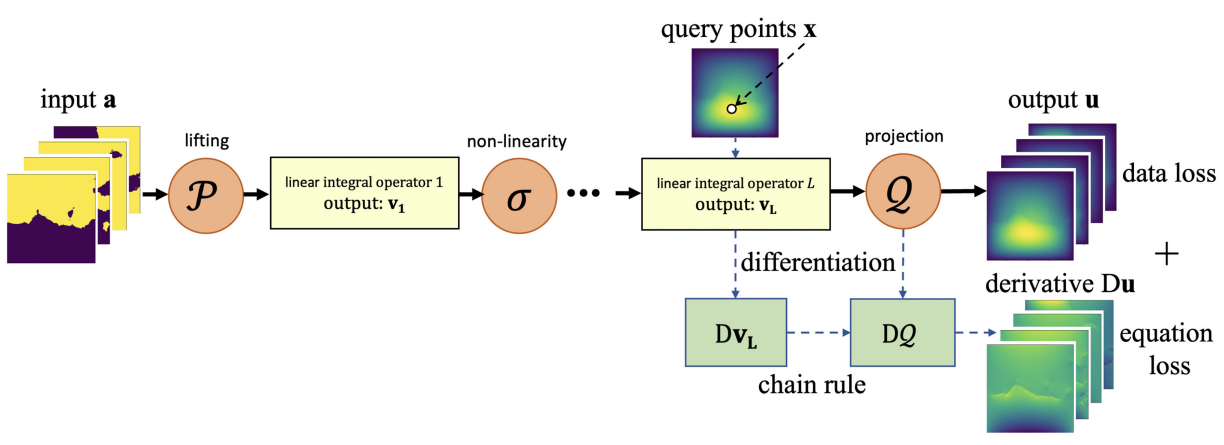
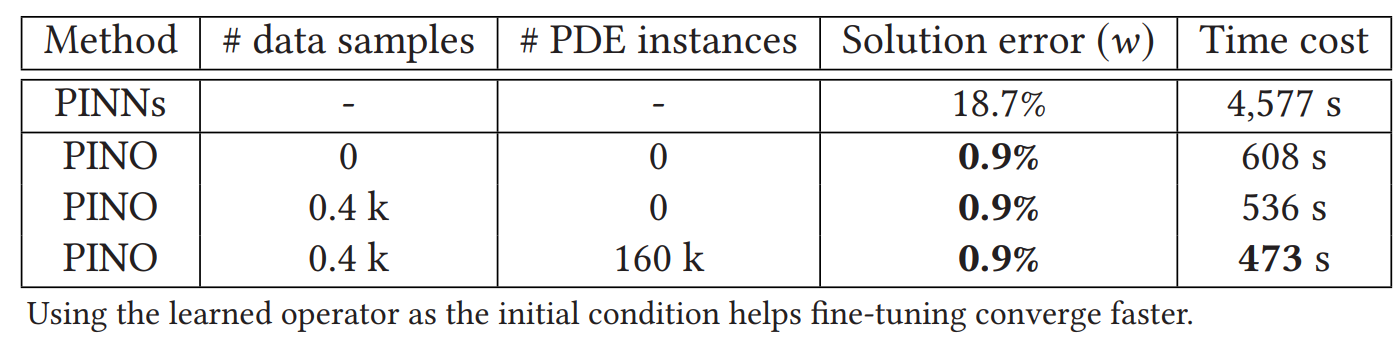
方法:论文提出了一种结合了物理信息和神经网络算子的新方法PINO,用于学习求解参数化偏微分方程(PDEs)的解算子。PINO利用神经算子框架,能够精确地近似给定PDE族的解算子,并且在零样本超分辨率下不降低准确性。
创新点:
-
PINO 是一种混合方法,它结合了训练数据和物理约束,来学习给定参数化 PDEs 家族的解算子。
-
PINO 使用傅里叶神经算子(FNO)框架,它是一个对任何连续算子的通用逼近器,并且在网格细化的极限中是离散化收敛的。
-
在准确性和速度方面,PINO 优于其他基于物理信息的学习方法,如 PINN、LAAF-PINN 和 SA-PINN。
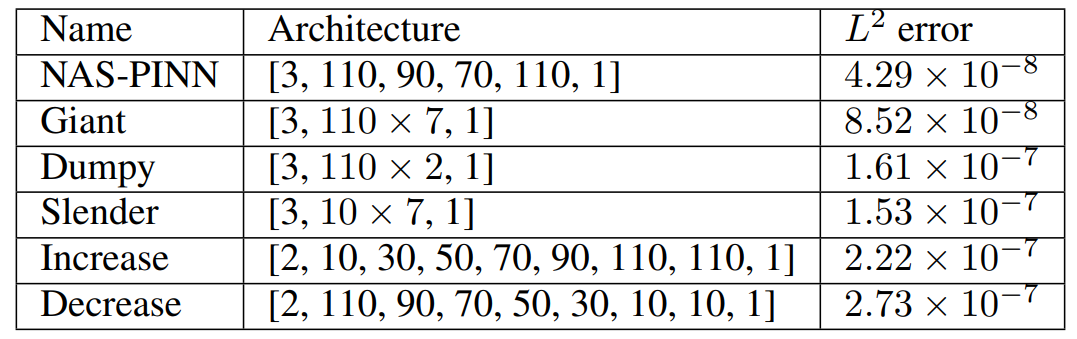
NAS-PINN: neural architecture search-guided physics-informed neural network for solving PDEs
方法:论文提出了一种新型的神经网络架构搜索方法,称为NAS-PINN,它用于求解偏微分方程(PDEs)。NAS-PINN通过自动搜索最优的神经网络架构来解决特定的PDEs问题。
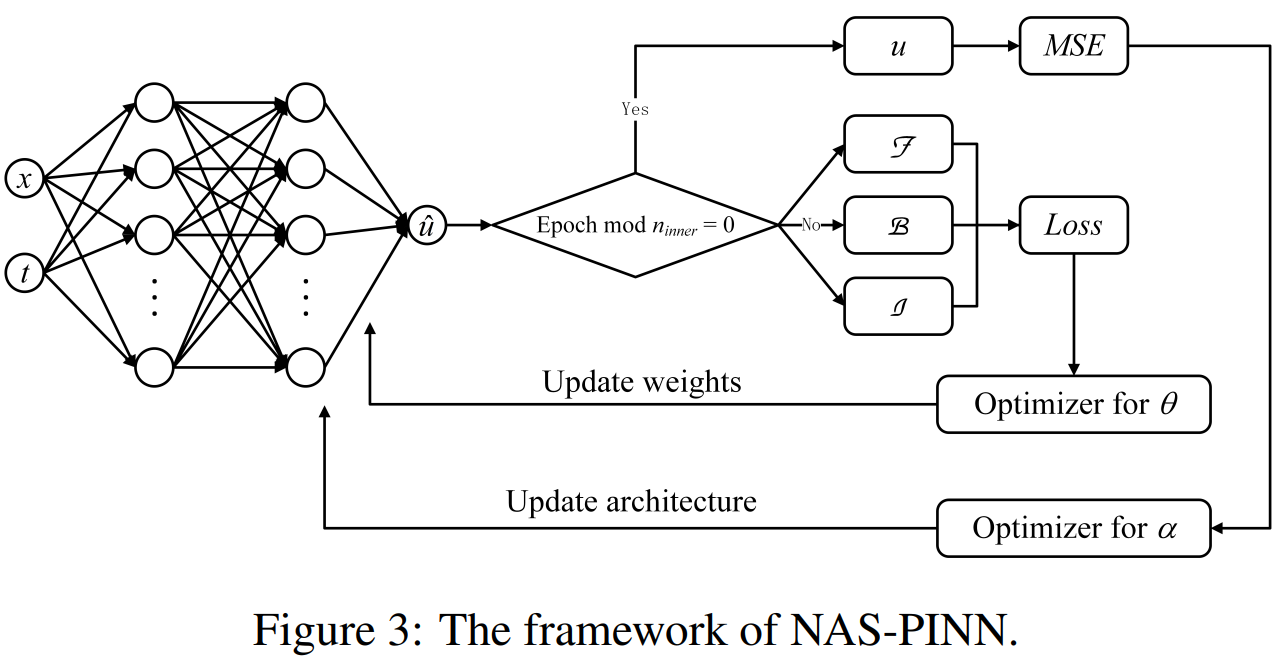
创新点:
-
提出了一种新的神经架构搜索方法,称为NAS-PINN。通过构建混合操作和引入掩码来实现不同形状张量的相加,将架构搜索问题转化为一个连续的双层优化问题。
-
在PINN框架中引入了空间信息。通过使用数值微分(ND)替代自动微分(AD),成功地将空间信息引入模型中,确保模型得到的解符合物理定律。
Solving partial differential equations with sampled neural networks
方法:论文研究了基于神经网络的偏微分方程(PDE)求解方法,提出了一种新的采样方法,通过随机采样内部权重来构建神经网络的基函数,并通过分离变量的方法解决时间相关问题。
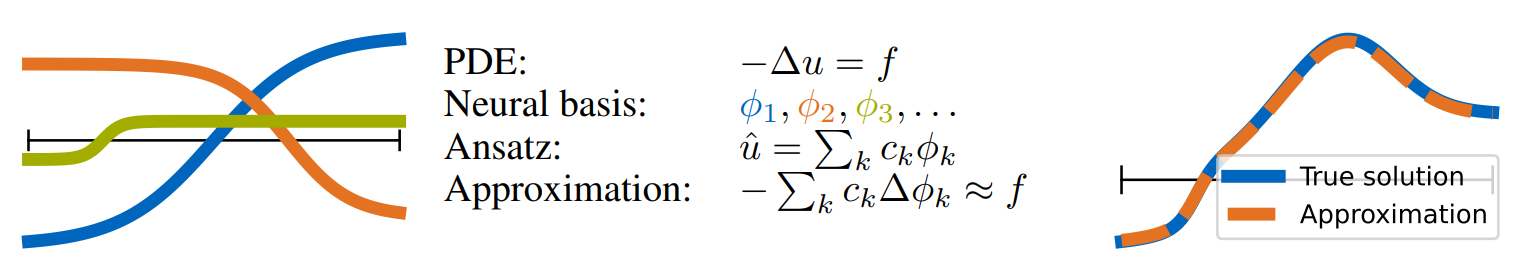
创新点:
-
通过对隐藏层的权重进行采样,提出了一种用于求解偏微分方程(PDE)的新方法。
-
对于静态线性PDE,通过求解一个线性问题来找到解,从而减少了参数的数量。
-
对于一般的时间依赖性PDE,通过在空间中随机采样ansatz函数,将问题简化为求解高维ODE。
关注下方《学姐带你玩AI》🚀🚀🚀
回复“物理微分”获取全部论文+开源代码
码字不易,欢迎大家点赞评论收藏









)


数值微分)




建议收藏!)

