问题一:
首先看一个最经典的问题:上台阶问题。P1255 数楼梯 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
我们首先看一下,如何用DFS的方法进行解题。
假设我们要上到第5级台阶:
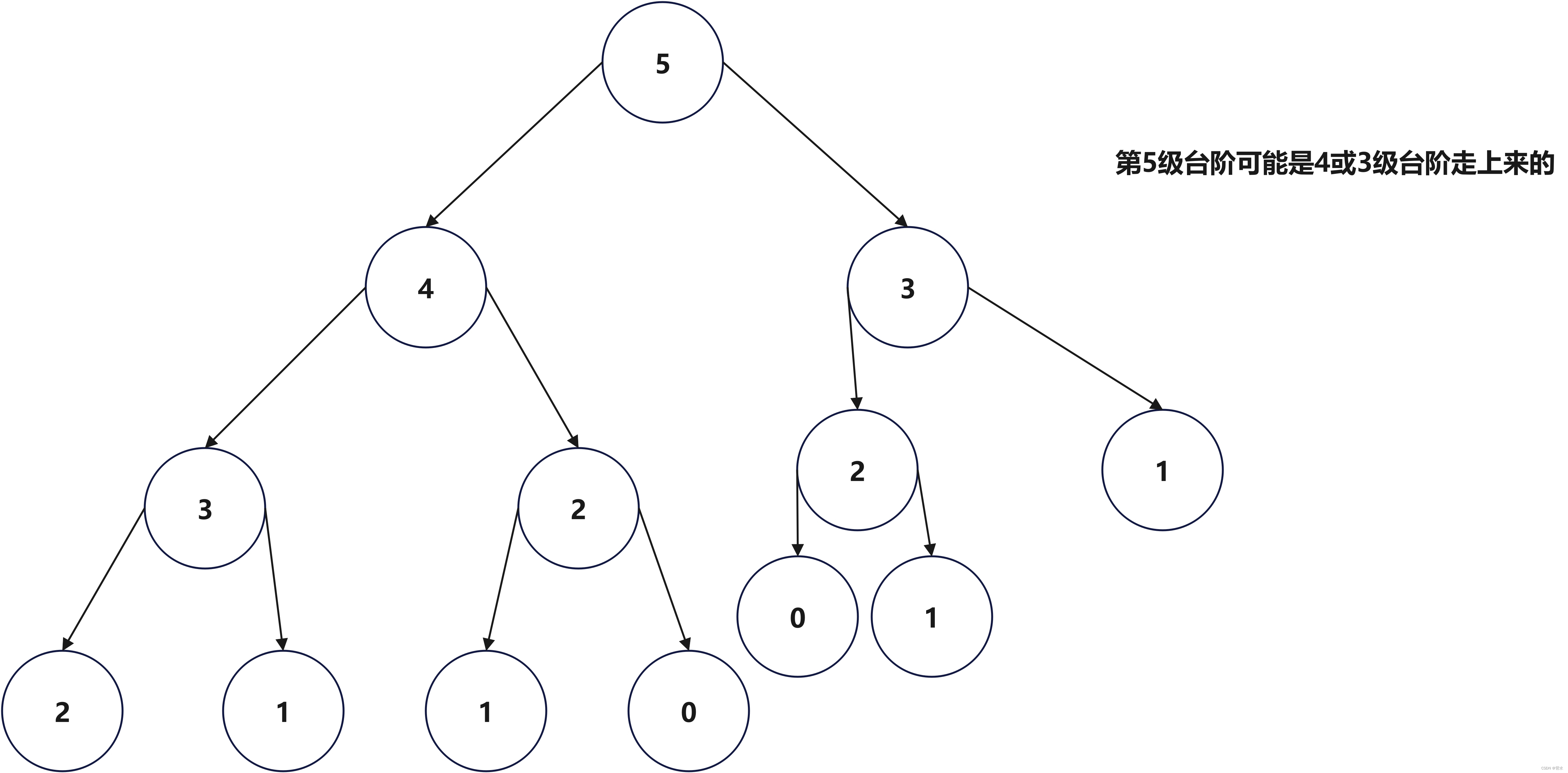
可以看出上到第五级台阶时,可能是由第4级上去的,也可能是从第3级上去的。接下来以此类推。
所有我们很容易想到一个方程:假设F(x)表示上到第X级台阶的方案数。那么不难看出:
F(x) = F(x-1) + F(x-2)
一开始不要多想直接按照常规的DFS进行,
#include<iostream>
using namespace std;
int n;
int dfs(int x)
{if(x==1) return 1;else if(x==2) return 2; return dfs(x-1) + dfs(x-2);
}int main()
{cin>>n;cout<<dfs(n)<<endl;return 0;
}但是这个过不了;
再看上面的图,发现很多都算了2遍,比如3。
那么来记忆化搜索:
问题二:
1049. 大盗阿福 - AcWing题库
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 𝑁 家店铺,每家店中都有一些现金。
阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
输入的第一行是一个整数 T𝑇,表示一共有 𝑇 组数据。
接下来的每组数据,第一行是一个整数 𝑁 ,表示一共有 𝑁 家店铺。
第二行是 𝑁 个被空格分开的正整数,表示每一家店铺中的现金数量。
每家店铺中的现金数量均不超过1000。
输出格式
对于每组数据,输出一行。
该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
输入样例:
2
3
1 8 2
4
10 7 6 14
输出样例:
8
24解答题目啦:
首先用DFS的思想想一下:
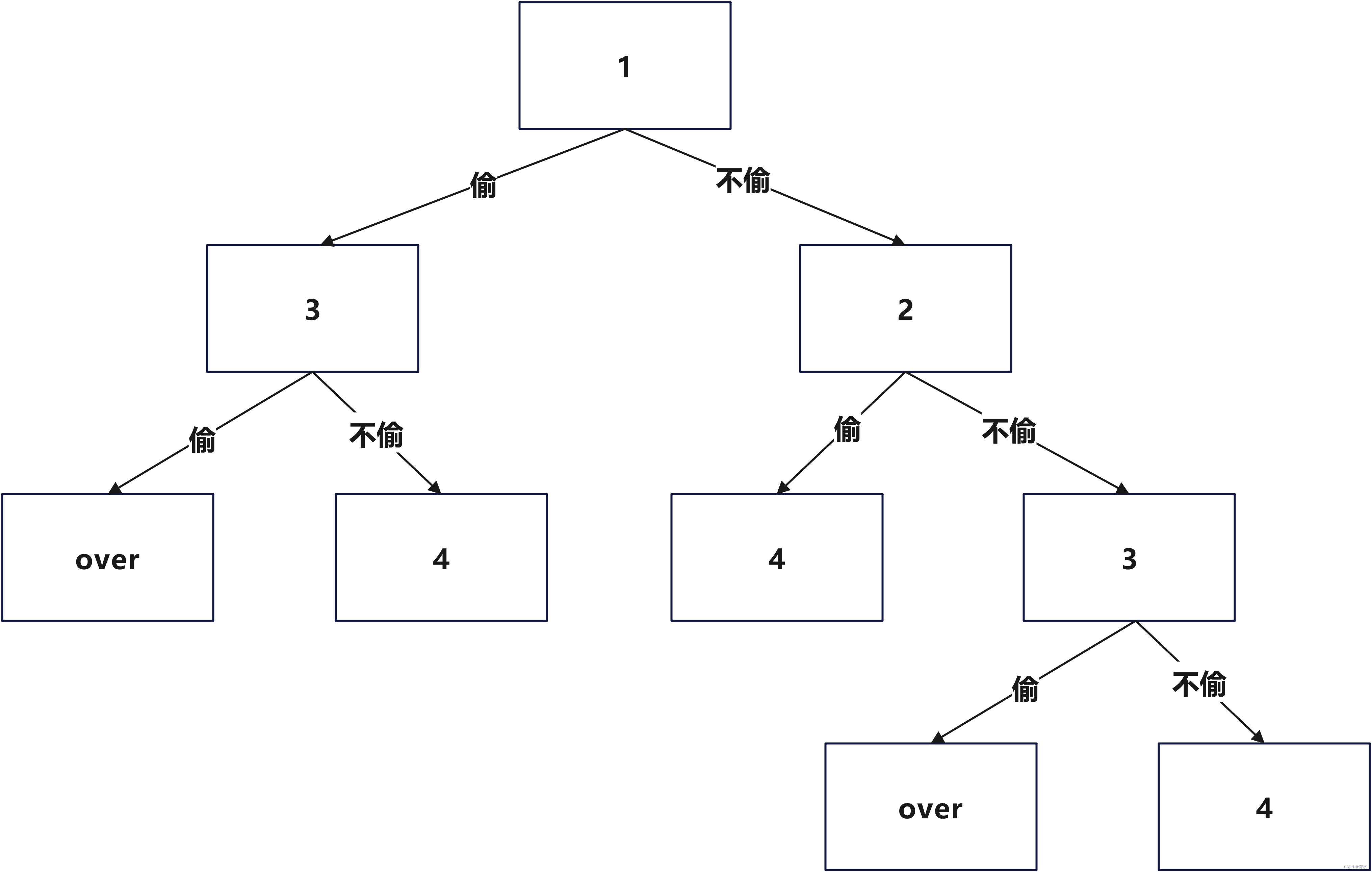
解释一下:
方块里面的标i记是第i家店。每个店铺都可以进行偷或不偷。但是!当偷了前一个店铺,那么这个店铺就不能再偷了。
还有一点很重要的要注意!我们这里是从第一家(1)先“分”到第4家或第3家,然后还要返回去。也就是说要确定递归的终点,这里可以想到如果到了倒数第一个(4)或倒数第2各(3)都要return 。
那么我们是不是也可以反过来递归呢?
答案当然可以啦。
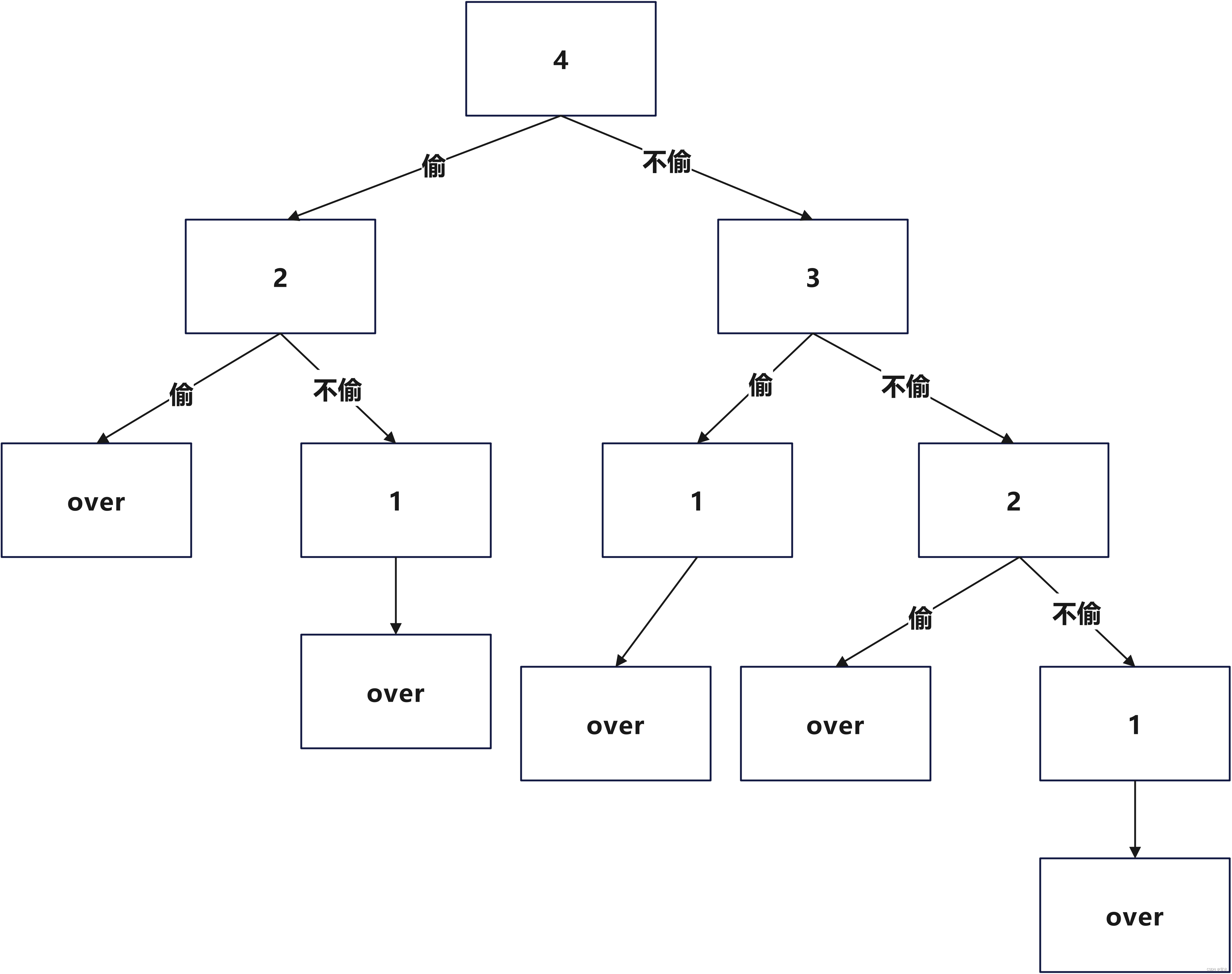
先看从1开始递归的:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100005;
int n;
int arr[N];
int dfs(int x)
{if(x>n) return 0;//注意这里为什么是只要x>n就可以了?return max(dfs(x+1),dfs(x+2) + arr[x]);
}
int main()
{int T;cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++) cin>>arr[i];cout<<dfs(1)<<endl; }return 0;
}
上面有个小细节:为什么当x>n就可以了呢?不是当此时选了3也就停止了吗?以及为什么这样就可以用dfs直接加上一个数了?
我们这样一步一步分析: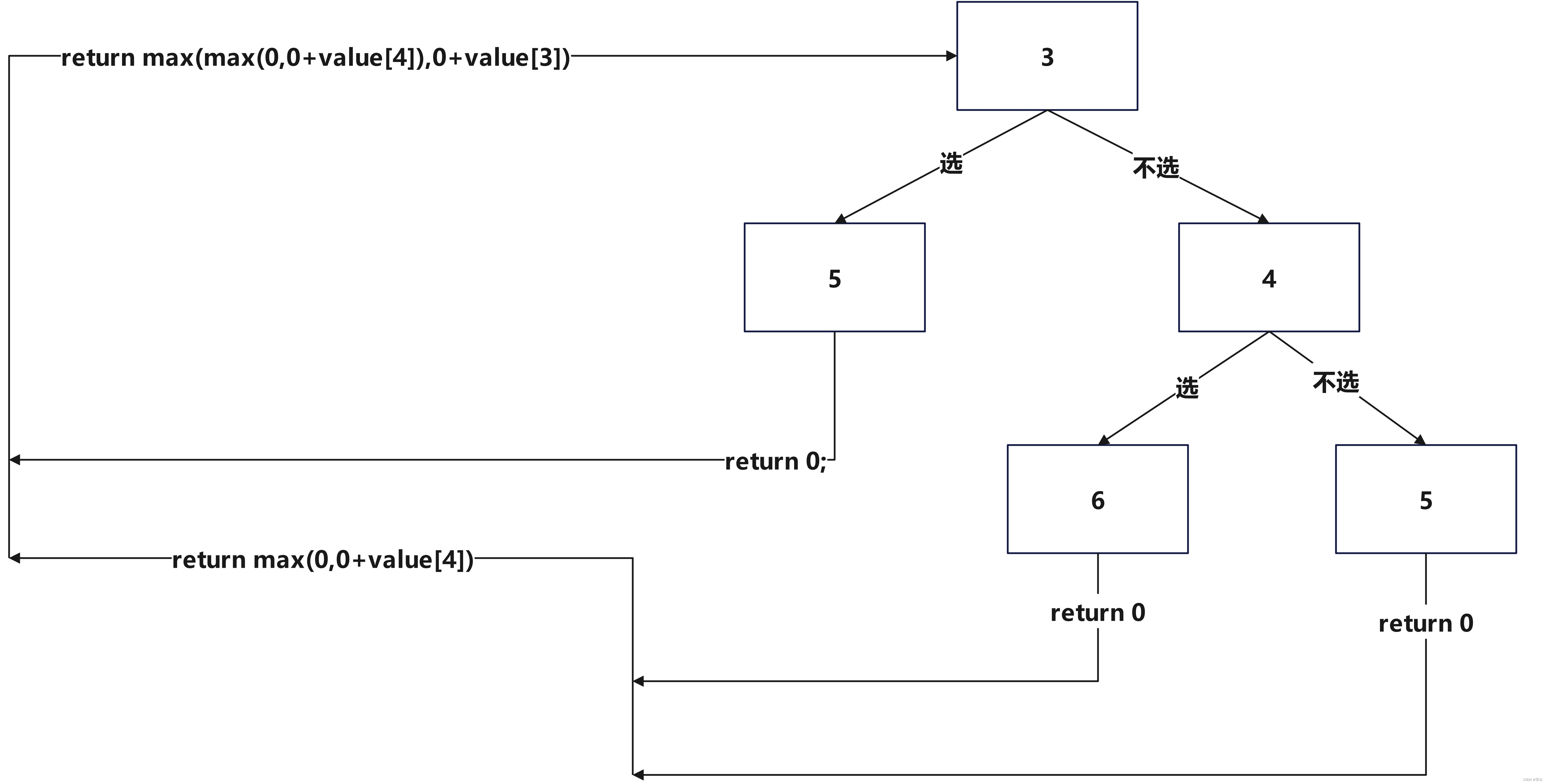
发现:4及以上的都必须是0,而选了3时下一个一定是5,所以直接递归0就OK。也不会执行下面的。
现在我们来记忆化搜索:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 100005;
int n;
int arr[N];
int mum[N];
int dfs(int x)
{if(mum[x]) return mum[x];int summ = 0; //创建一个变量用来存储当前节点的数值。if(x>n) summ = 0; //如果越界那么值为0;else summ = max(dfs(x+1),dfs(x+2) + arr[x]);//否则将DFS的值赋值给summum[x]=summ; //将summ的值赋值给记忆化数组return summ; //返回当前层的值。注意如何越界了就不会走else后面的了。这里要和不加else区分开
}
int main()
{int T;cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++) cin>>arr[i];cout<<dfs(1)<<endl; memset(mum,0,sizeof(mum));}return 0;
}有的小伙伴可能会这样想,我要记录最大值,那么我可不可以在DFS函数上面加一个参数呢?这个参数用来记录当前的最大值。
这个思想是可以的,但是我们想一下:加上这个参数能给我们省下什么?加上一个参数,那就说明此时的状态(就是此时的层数和价格组成的笛卡尔积)是一个节点,我们进行记忆化存储的前提是什么?是要存什么?在上面的图中可以看出是要存节点的值(哪一层),现在多加了一个参数,那是不是要用二维数组来存储啊?
而且我们前面在DFS函数中加参数是为了是什么?
是因为这个参数可以影响我们的递归的进行,比如(x1,y1)这个坐标。当然要两个值,因为x和y都不能超出界限,一旦超出那就要return 。和我们这一题比较一下,我们加上当前我们偷的最大值有有什么影响吗?这个最大值没有限制我们递归的进行,所以是不需要加上的,加了反而多此一举。
我们要记住:
当想要剪枝时,在DFS函数中尽可能多的加入可以判断剪枝的参数。
当要记忆化存储时,在DFS函数中尽可能少的加入参数。
接下来,进阶,DP!
对于这个图:

我们的DFS是从4 --> 1 ,然后从1-->4,那我们能不能直接从1到4呢?
答案是可以的:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 100005;
int n;
int arr[N];
int mum[N];
int dp[N];
//int dfs(int x)
//{
// if(mum[x]) return mum[x];
// int summ = 0;
// if(x>n) summ = 0;
// else summ = max(dfs(x+1),dfs(x+2) + arr[x]);
// mum[x]=summ;
// return summ;
//}
int main()
{int T;cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++) cin>>arr[i];
// cout<<dfs(1)<<endl;
// memset(mum,0,sizeof(mum));for(int i=1;i<=n;i++){//dp[i] = max(dp[i-1],dp[i-2] + arr[i-2])//这里i同时加2dp[i+2] = max(dp[i+1],dp[i] + arr[i]);}cout<<dp[n+2]<<endl;;}return 0;
}可能很多人直接接触DP时,很不理解这个给状态转移方程到底咋来的,我们观察上面,它不就是DFS直接从最底层向上推得来的吗?



















