粒子扩展卡尔曼滤波|MATLAB代码

粒子滤波PF与扩展卡尔曼滤波EKF结合
下载链接：https://download.csdn.net/download/callmeup/89512392

粒子滤波

粒子滤波是一种用于估计状态变量的非线性滤波方法。它通过引入一组粒子来近似表示概率分布，从而利用蒙特卡洛方法进行状态估计。粒子滤波的主要思想是根据系统的状态转移方程和观测方程，在每个时间步上对每个粒子进行状态更新和权重更新。

具体而言，粒子滤波包括以下步骤：

初始化：根据先验知识或测量数据，生成一组初始粒子，并为每个粒子赋予相同的权重。
预测：使用系统的状态转移方程对每个粒子进行状态更新。根据系统的动力学模型，可以通过添加噪声来模拟系统的不确定性。
权重更新：使用观测方程计算每个粒子的观测值，并根据观测值与实际观测值的差异来更新每个粒子的权重。差异越小，权重越高。
重采样：根据粒子的权重，以一定的概率进行重采样，以保留具有较高权重的粒子，并且生成新的粒子来填补权重较低的区域。
估计：根据粒子的权重，可以使用加权平均或最大权重对状态进行估计。

通过不断重复上述步骤，粒子滤波可以逐步收敛到目标状态的概率分布，从而实现状态估计。粒子滤波在非线性问题和非高斯问题中表现优秀，并且可以适用于多传感器融合、目标跟踪、机器人定位等领域。

卡尔曼滤波与EKF

卡尔曼滤波（Kalman Filter）和扩展卡尔曼滤波（Extended Kalman Filter，EKF）是用于状态估计的常见方法。

卡尔曼滤波是一种最优的线性滤波器，用于从包含噪声的测量数据中估计系统的状态。它基于一个线性的状态空间模型，假设系统的状态变量和观测变量服从线性的高斯分布。卡尔曼滤波器通过对观测数据和系统模型进行融合，以得到最优的系统状态估计结果。

扩展卡尔曼滤波是卡尔曼滤波的非线性扩展。它在模型中引入了非线性函数，使得系统模型和观测模型可以处理非线性问题。在EKF中，通过线性化非线性函数，将非线性问题转化为线性问题，然后利用卡尔曼滤波的方法进行状态估计。

EKF常用于非线性系统的状态估计，例如机器人定位和导航、目标跟踪等领域。它在实际应用中具有一定的稳定性和鲁棒性，但也存在一些缺点，如对初始状态估计的依赖性较强，容易出现估计误差累积的问题。

总之，卡尔曼滤波和EKF是常用的状态估计方法，其中卡尔曼滤波适用于线性系统，EKF适用于非线性系统。它们在估计系统状态方面具有一定的优势和适用性，但也需要根据具体问题选择合适的方法。

粒子扩展卡尔曼滤波

粒子滤波PF与扩展卡尔曼滤波EKF结合，命名为PEKF，主要思想是：
对状态量进行采样，并对其粒子进行EKF的求解，得到的粒子再经过加权平均得到估计的状态量。状态协方差、一步转移噪声协方差、观测协方差均遵循EKF

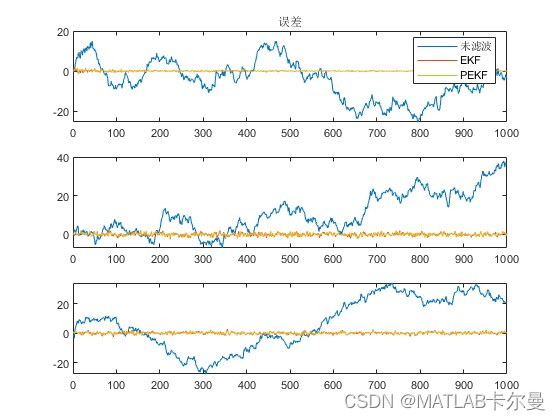
效果

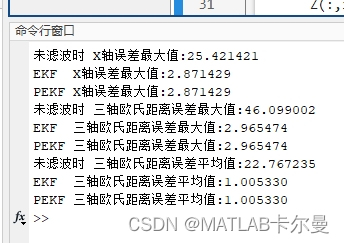
粒子数=1时，PEKF=EKF，两者效果相同，估计误差的统计特性也相同：
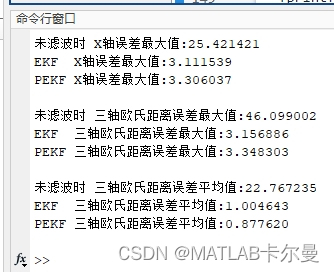
请添加图片描述
粒子数=10时，各有千秋，但是PEKF的三轴欧氏距离误差平均值更低：

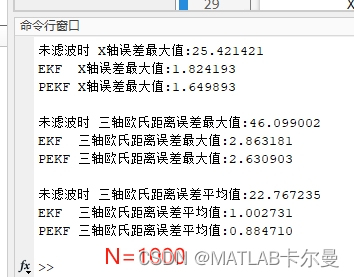
粒子数=1000时，PEKF的效果明显更好：

状态曲线如下：

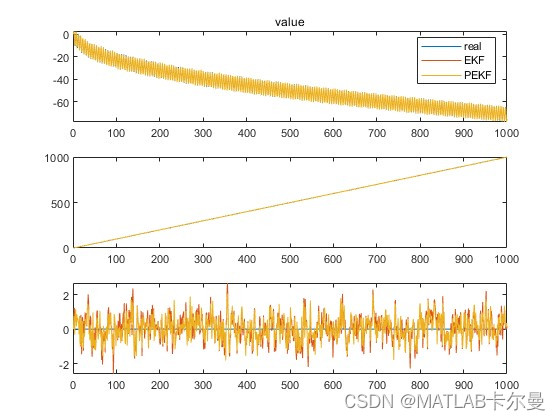
误差曲线如下：

部分程序源代码

% EKF与PF的融合，粒子扩展卡尔曼滤波PEKF
% author:Evand
% 作者联系方式：evandjiang@qq.com（除前期达成一致外，咨询需付费）
% 2024-7-3/Ver1
clear;clc;close all;
rng(0);
%% 参数设置
N = 1000; %粒子总数
t = 1:1:1000;
Q = 1*diag([1,1,1]);w_=sqrt(Q)*randn(size(Q,1),length(t));
w_pf =