假设我们有一个简单的信号，由两个不同频率的正弦波组成，我们希望通过傅里叶变换来分析其频谱。

示例信号

假设我们有一个信号 ：

这个信号由两个频率成分组成：一个50 Hz的正弦波和一个120 Hz的正弦波，后者的振幅是前者的一半。

采样和离散化

首先，我们需要将连续信号离散化，以便进行计算。假设采样频率为1000 Hz，即每秒采样1000次。我们采样1秒钟，得到1000个样本点。

采样得到的离散信号为：

计算离散傅里叶变换（DFT）

我们使用离散傅里叶变换来将离散信号转换到频域：

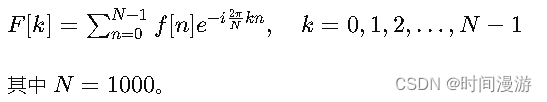
实际计算（使用Python）

为了方便，我们使用Python和NumPy库来进行计算：

import numpy as np
import matplotlib.pyplot as plt# 参数设置
fs = 1000  # 采样频率 (Hz)
t = np.linspace(0, 1, fs, endpoint=False)  # 采样点
f = np.cos(2 * np.pi * 50 * t) + 0.5 * np.cos(2 * np.pi * 120 * t)  # 信号# 计算傅里叶变换
F = np.fft.fft(f)# 计算频率
frequencies = np.fft.fftfreq(fs, 1/fs)# 绘制结果
plt.figure(figsize=(12, 6))
plt.plot(frequencies, np.abs(F))
plt.title('Frequency Domain')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.grid(True)
plt.show()

结果分析

通过计算傅里叶变换，我们得到频域表示 F(ω)，并绘制其频谱图。结果显示在频率50 Hz和120 Hz处有两个峰值，对应于原始信号中的两个频率成分。

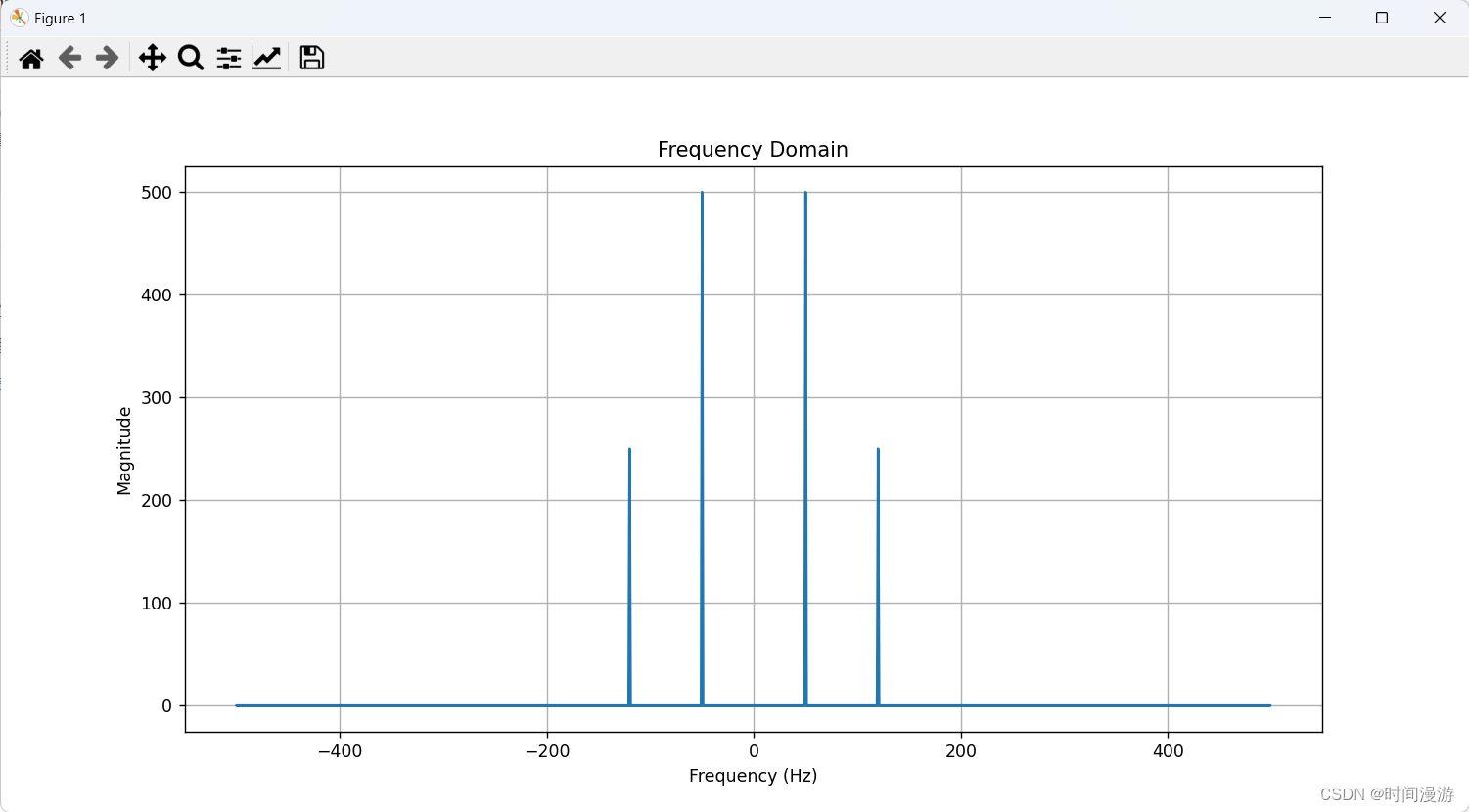
np.fft.fftfreq 函数生成一个数组，该数组包含傅里叶变换中对应的频率。对于一个长度为 N 的信号，其频率分量的索引范围是 −N/2 到 N/2−1

np.abs(F) 是计算复数数组 F 的绝对值（或模）的函数。在傅里叶变换的上下文中，这通常用于获取信号的幅度谱。