一、快速排序的思想
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
二、快速排序的三种实现方法
2.1、Hoare
思想:取最左边key为基准值,用right指针找比key值小的元素,用left指针找比key位置大的元素,
将两位置值进行交换,最后,将key值放在二者相遇位置上,就可保证key左边都是比key小的值,
右边都是比key大的值,然后进行递归即可实现,从相遇点分割成两部分,在分别对左右两部分重
复上述排序。

代码实现 :
void Swap(int* p1, int* p2)
{int temp = *p1;*p1 = *p2;*p2 = temp;
}
//Hoare
int partSort1(int* a, int left, int right)
{int key = left;while (right > left){//从右往左找小while (right > left && a[right] >= a[key]){right--;}//从左往右找大while (right > left && a[left] <= a[key]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[key]);return left;
}void QuickSort(int* arr, int begin,int end)
{if (begin >= end){return;}int keyi = partSort1(arr, begin, end);QuickSort(arr, begin, keyi - 1);QuickSort(arr, keyi + 1, end);
}
2.2、挖坑法
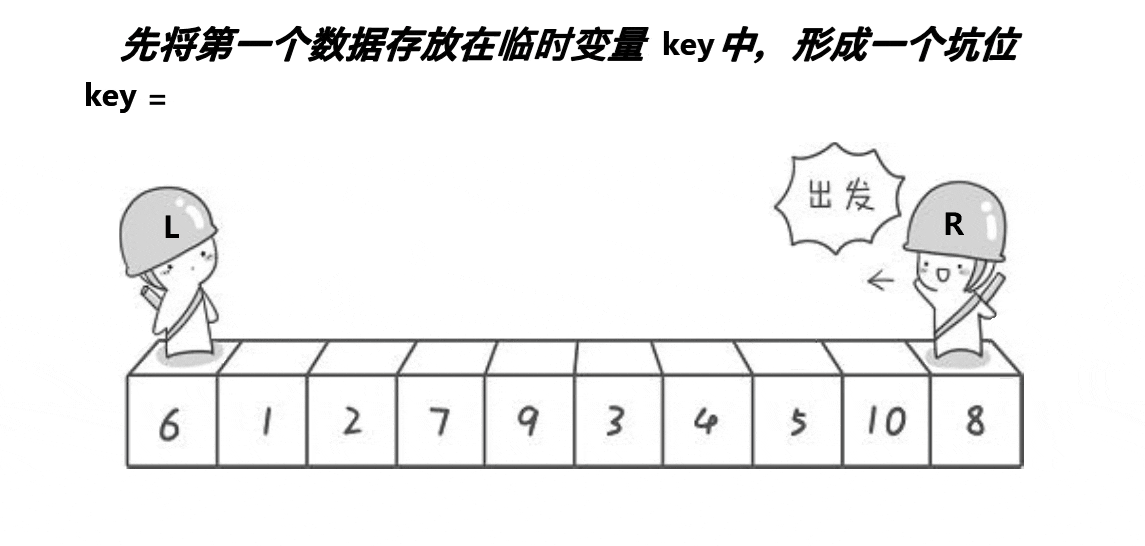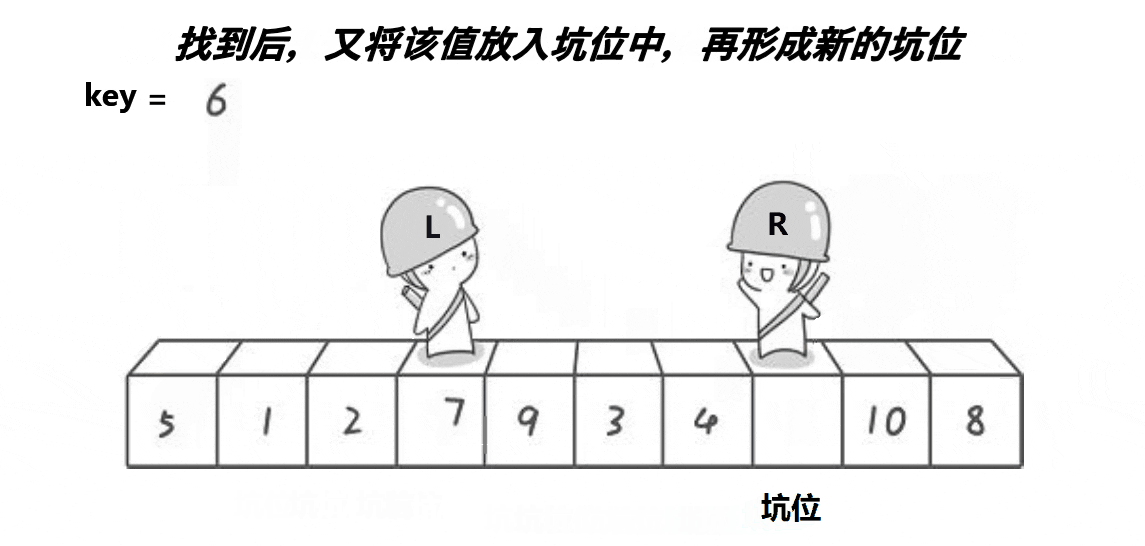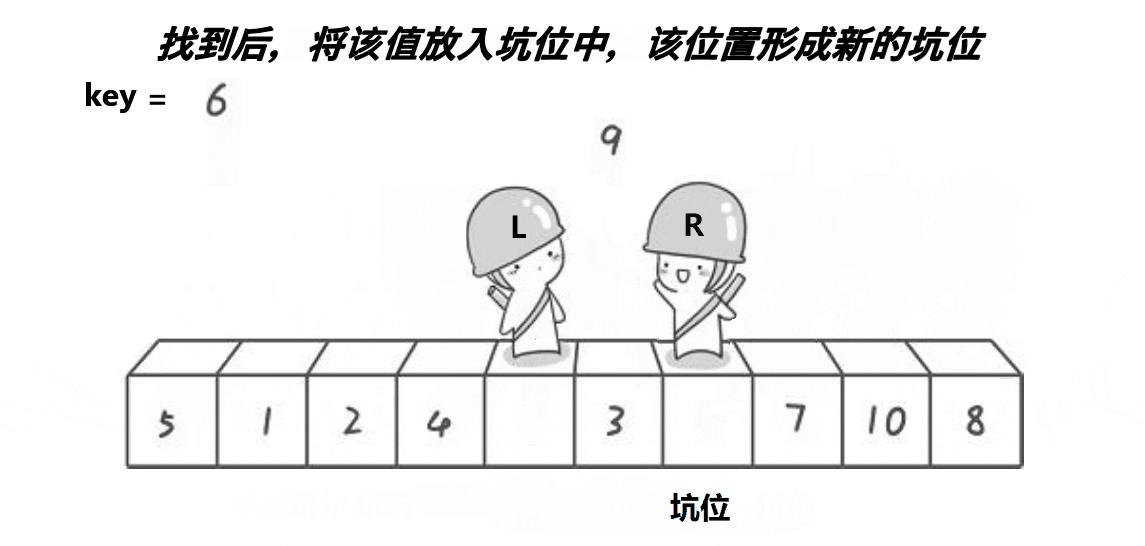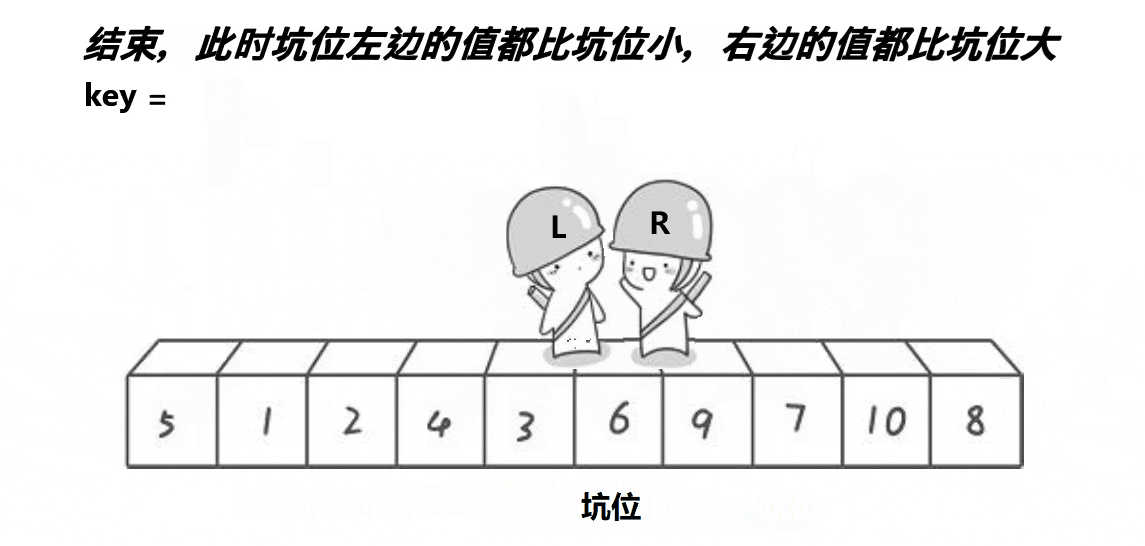
思想:取最左边或最右边值做key,右边形成一个坑,定义两个指针left、right指向头和尾。右边找
小值放到左边坑中右边形成新坑,左边找大值放到右边左边形成新坑,将key放到相遇位置。这时
key左边值均小于key,右边值均大于key。
 代码实现:
代码实现:
void Swap(int* p1, int* p2)
{int temp = *p1;*p1 = *p2;*p2 = temp;
}//挖坑法
int partSort2(int* a, int left, int right)
{int hole = left;int key = a[left];while (right > left){//从右往左找小while (right > left && a[right] >= key){right--;}a[hole] = a[right];hole = right;//从左往右找大while (right > left && a[left] <= key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}void QuickSort(int* arr, int begin,int end)
{if (begin >= end){return;}int keyi = partSort2(arr, begin, end);QuickSort(arr, begin, keyi - 1);QuickSort(arr, keyi + 1, end);
}
2.3、双指针法
思想:
1.选择数组中的第一个元素arr[startIndex]作为轴(pivot)
2.左指针为left,从最左边开始寻找第一个比pivot大的数
3.右指针为right,从最右面的一个元素开始向左寻找第一个小于等于pivot的数值
4.经过2,3两个步骤后,将会出现以下两种情况
(1):left和right没有相遇,此时进行交换,swap(arr,left,right);
(2):left和right相遇,做swap(arr,startIndex,left),然后返回left
5.partition中返回pivot用于分割数组,下一次用于排序的数组被分割为(startIndex,pivot-1),(pivot+1,endIndex)两段,进行递归操作

代码实现:
void Swap(int* p1, int* p2)
{int temp = *p1;*p1 = *p2;*p2 = temp;
}int partSort3(int* a, int left, int right)
{int prev = left;int cur = prev + 1;int key = left;while (cur <= right){if (a[cur] < a[key] && ++prev != cur){Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[prev], &a[key]);return prev;
}void QuickSort(int* arr, int begin,int end)
{if (begin >= end){return;int keyi = partSort3(arr, begin, end);QuickSort(arr, begin, keyi - 1);QuickSort(arr, keyi + 1, end);
}三、快速排序的优化
3.1、三数取中
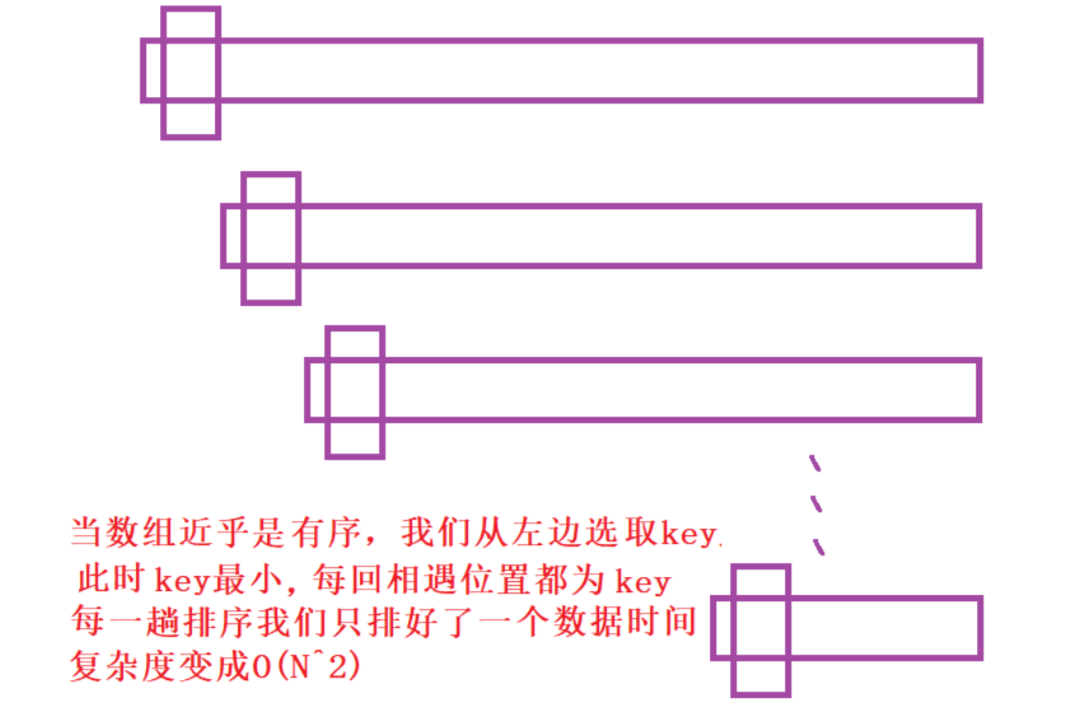
当要排序的数组有序或者相对有序,比如我们要把一个逆序的数组按顺序排列,这时我们如果还选
择left为key的话,效率就会非常的低。我们要排除这种低效的可能就要让Key的值相对靠中间一
点,对此我们可以在实现一个函数,选择处left ,right ,和mid三个数中数值中间的那个数。用这个
数作为key就会避免我们遇到的这类问题。
代码实现:
//三数取中
int Getmid(int* a, int left, int right)
{int mid = (left + right) / 2;// left mid rightif (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]) // mid是最大值{return left;}else{return right;}}else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]) // mid是最小{return left;}else{return right;}}
}对此我们就可以改进上面的三种方法,都可以在三种方法的开头添加这段代码,使之让key为靠中间的数,避免数组为有序的排序时间效率低的问题。
int midi = Getmid(a, left, right);Swap(&a[left], &a[midi]);3.2、小区间优化
我们递归的深度越高效率越高,但是我们刚开始递归时深度很低,所以效率低下,所以我们可以采用高深度的时候用快速排序,在低深度的时候用直接插入排序,会对运行效率有所提高。
void QuickSort(int* a, int begain, int end)
{if (begain >= end)return;//小区间优化法 当数据量比较大的时候可以通过调整参数(20),来减小递归次数,提高性能if ((end - begain) > 20){int meeti = HoareSort(a, begain, end);QuickSort(a, begain, meeti - 1);QuickSort(a, meeti + 1, end);}else{//数量比较少的时候用直接插入来排序InsertSort(a + begain, end - begain + 1);}}
四、非递归实现快速排序
递归需要在栈上为函数开辟空间,32位下,栈可使用的内存大小不超过2G,如果递归较深,依然可能会发生栈溢出,这个时候递归排序就不大适用,所以需要非递归出场。
利用栈来存储区间下标,代码如下:要注意先数组头,后入数组尾。出栈时栈顶的数据为数组尾,在出才为头位置下标。
代码如下:
//交换函数
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}//三数取中
int GetMinIndex(int* arr, int left, int right)
{int mid = (left + right) >> 1;if (arr[left] < arr[mid]){if (arr[mid] < arr[right]){return mid;}if (arr[left] < arr[right] && arr[right] < arr[mid]){return right;}return left;}else//arr[left] >= arr[mid]{if (arr[left] < arr[right]){return left;}if (arr[mid] < arr[right] && arr[right] < arr[left]){return right;}return mid;}
}//快排非递归
void QuickSort(int* arr, int n)
{ST st;StackInit(&st);//把左右区间压栈,先压右边StackPush(&st, n - 1);//后压左边StackPush(&st, 0);//只要栈不为空,就继续分割排序while (!StackEmpty(&st)){//从栈里面取出左右区间int left = StackTop(&st);StackPop(&st);int right = StackTop(&st);StackPop(&st);int index = GetMinIndex(arr, left, right);//因为我们下面的逻辑都是把第一个数作为key,//为了避免改动代码,这里我们直接交换就可以Swap(&arr[left], &arr[index]);//开始单趟排序int begin = left;int end = right;int pivot = begin;int key = arr[begin];while (begin < end){//end开始找小while (begin < end && arr[end] >= key){end--;}arr[pivot] = arr[end];pivot = end;//begin开始找大while (begin < end && arr[begin] <= key){begin++;}arr[pivot] = arr[begin];pivot = begin;}pivot = begin;arr[pivot] = key;//区间分为[left,pivot-1]pivot[pivot+1,right]//利用循环继续分割区间//先入右子区间if (pivot + 1 < right){//说明右子区间不止一个数//先入右边边界StackPush(&st, right);//再入左边边界StackPush(&st, pivot+1);}//再入左子区间if (left < pivot-1){//说明左子区间不止一个数//先入右边边界StackPush(&st, pivot-1);//再入左边边界StackPush(&st, left);} }StackDestory(&st);
}
五、时间复杂度
快速排序的时间复杂度:
最坏情况下,时间复杂度是O(n^2); (逆序)
最优情况下,时间复杂度是O(nlogn);
平均时间复杂度是O(nlogn);
快速排序是时间复杂度:O(logn)



)

)
)


 AutoGPT和AgentGPT)









