支持向量回归原理详解及Python代码示例

支持向量回归原理详解

支持向量回归（Support Vector Regression, SVR）是支持向量机（SVM）的一种扩展，用于回归问题。SVR通过寻找一个最佳的回归超平面，使得尽可能多的数据点落在超平面附近的ε-管内，从而达到预测连续值的目的。

支持向量回归原理详解

1. 支持向量回归的基本概念

2. 支持向量回归的数学表达

3. 支持向量回归的损失函数

4. 核函数

5. 参数选择

Python代码示例

代码解释

1. 支持向量回归的基本概念

SVR的核心思想是通过对输入空间进行映射，并在高维空间中寻找一个最优的回归超平面。SVR的目标是平衡模型复杂度和误差，最终得到一个具有良好泛化能力的回归模型。

2. 支持向量回归的数学表达

SVR的目标是找到一个函数 f(x)=w⋅x+b ，使得所有数据点 (xi,yi)的预测误差在ε以内，同时最小化 ∥w∥2。

SVR的优化目标可以表示为：

在约束条件：

其中， ξi和 ξi∗ 是松弛变量，用于处理那些无法落在ε管内的数据点。

3. 支持向量回归的损失函数

SVR使用ε不敏感损失函数（ε-insensitive loss function）来忽略绝对误差小于ε的数据点。损失函数可以表示为：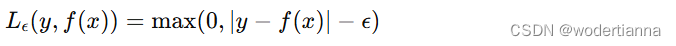

4. 核函数

SVR可以通过核函数（Kernel Function）将输入特征映射到高维空间，从而处理非线性问题。常用的核函数有线性核、多项式核、高斯核（RBF）等。

5. 参数选择

SVR的主要参数包括：

C：正则化参数，控制模型复杂度与误差之间的权衡。
ε：ε-不敏感区域的宽度，控制模型对误差的容忍度。
核参数：如高斯核中的γ参数，控制高维空间中的决策边界形状。

Python代码示例

以下是一个完整的Python代码示例：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split# 生成一些示例数据
np.random.seed(0)
x = np.sort(5 * np.random.rand(100, 1), axis=0)
y = np.sin(x).ravel()
y[::5] += 3 * (0.5 - np.random.rand(20))  # 添加噪声# 可视化原始数据
plt.scatter(x, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.title("Original Data")
plt.show()# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)# 创建支持向量回归模型并进行拟合
svr_rbf = SVR(kernel='rbf', C=100, gamma=0.1, epsilon=0.1)
svr_rbf.fit(x_train, y_train)# 预测结果
y_train_pred = svr_rbf.predict(x_train)
y_test_pred = svr_rbf.predict(x_test)# 可视化拟合结果
x_test_sorted = np.sort(x_test, axis=0)
y_test_pred_sorted = svr_rbf.predict(x_test_sorted)plt.figure()
plt.scatter(x_train, y_train, s=20, edgecolor="black", c="darkorange", label="train data")
plt.scatter(x_test, y_test, s=20, edgecolor="black", c="blue", label="test data")
plt.plot(x_test_sorted, y_test_pred_sorted, color="green", label="predictions", linewidth=2)
plt.title("Support Vector Regression")
plt.legend()
plt.show()# 打印模型参数和均方误差
print("Train Mean Squared Error:", mean_squared_error(y_train, y_train_pred))
print("Test Mean Squared Error:", mean_squared_error(y_test, y_test_pred))

代码解释

数据生成：
- 生成100个随机点，并将这些点排序。
- 使用正弦函数生成目标值，并在部分数据上添加随机噪声以增加数据的复杂性。
数据可视化：
- 绘制生成的原始数据点，用散点图表示。
数据划分：
- 将数据划分为训练集和测试集，训练集占80%，测试集占20%。
模型训练：
- 使用SVR类构建支持向量回归模型，选择高斯核（RBF），设置参数C=100，gamma=0.1，epsilon=0.1。
- 在训练数据上进行拟合。
结果预测：
- 在训练集和测试集上进行预测，生成预测结果。
- 对测试数据按顺序排序，以便于绘制预测曲线。
可视化拟合结果：
- 绘制训练数据、测试数据及模型的预测结果，观察模型的拟合效果。
模型评估：
- 计算并打印训练集和测试集的均方误差（MSE），评估模型的拟合性能。