首先连通块,所以点分治肯定是
Trick1 钦定选根的连通块dp
对于钦定选根的连通块dp,有一种常见思路
先对原树求其dfn序,按dfn序倒序求解
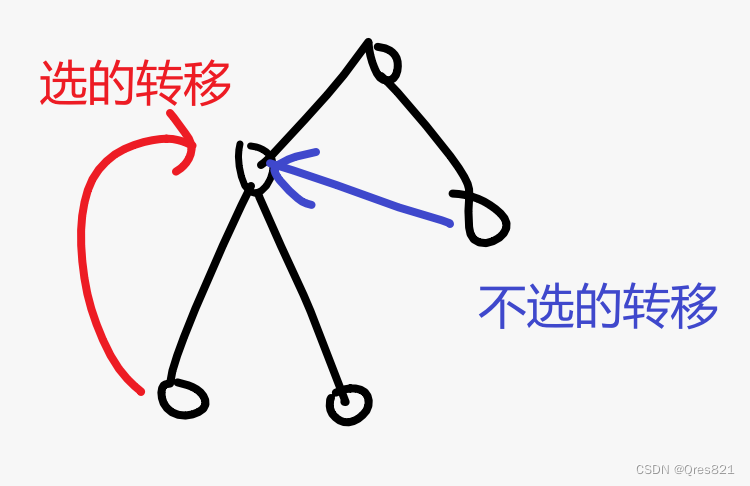
具体的,对于当前点 i i i(注意这里都是指dfn序),我们可以钦定 i i i 是否选
如果 i i i 选,就由 i + 1 i+1 i+1,也就是 i i i 的第一个儿子转移过来(因为只有他选他子树才可能被选)
如果 i i i 不选,就由 i + w i i+w_i i+wi 转移过来,因为他的儿子必然不会被选
至于 i i i 和 i + w i i+w_i i+wi 同时选的情况,我们在 i + 1 i+1 i+1 那里已经算了
对于 i i i 和 i + w i i+w_i i+wi 是否连通的问题,当他们的lca都被选时,则他们必然也被选,这里一定会在他们祖先那里被算到
Trick 2 对于乘积类dp的根号优化方法
考虑直接 d p [ x ] [ i ] dp[x][i] dp[x][i], i i i 值域过大。
但我们可以拆分 f ( x , i ) , g ( x , i ) f(x,i),g(x,i) f(x,i),g(x,i),代表已选乘积为 i i i / 还可以选乘积为 i i i 的方案数
这样状态直接压成 O ( m ) O(\sqrt m) O(m)
其实也可以用整除分块的证明进行预处理
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 4010
#define M 1510
#define mo (int)(1e9+7)
int n, m, i, j, k, T;
int Rt, rt, f[N][M], g[N][M];
int mx[N], w[N], dfn[N], tot, sum, u, v;
int sq, p[N], v1, v2, a[N], ans;
vector<int>G[N]; void dfs(int x, int fa) {w[x]=mx[x]=1; for(int y : G[x]) {if(y==fa || p[y]) continue; dfs(y, x); w[x]+=w[y]; mx[x]=max(mx[x], w[y]); }mx[x]=max(mx[x], sum-w[x]); if(mx[x]<mx[rt]) rt=x;
}void dfs2(int x, int fa) {dfn[++tot]=x; for(int y: G[x]) if(y!=fa && !p[y]) dfs2(y, x);
}void Add(int &a, int b) {a=(a+b)%mo;
}void dfz(int x) {
// printf("> %lld\n", x); int i, j, u; tot=0; dfs(x, 0); dfs2(x, 0);
// for(i=1; i<=tot; ++i) printf("%lld ", dfn[i]); printf("\n"); for(i=0; i<=tot+5; ++i)for(j=0; j<=sq+5; ++j) f[i][j]=g[i][j]=0;
// f[tot+1][1]=1; for(i=tot; i>=1; --i) {u=dfn[i]; if(a[u]>sq) Add(g[i][m/a[u]], 1); else Add(f[i][a[u]], 1); for(j=1; j<=sq; ++j) {v1=i+1; v2=i+w[u]; if(j*a[u]>sq && j*a[u]<=m) Add(g[i][m/(j*a[u])], f[v1][j]); else if(j*a[u]<=m) Add(f[i][j*a[u]], f[v1][j]); if(j>=a[u]) Add(g[i][j/a[u]], g[v1][j]);
//
//
// Add(f[i][j], f[v2][j]); Add(g[i][j], g[v2][j]); }}for(i=1; i<=sq; ++i) Add(ans, f[1][i]+g[1][i]); // printf("# %lld : %lld\n", x, ans); dfs(x, 0); p[x]=1; for(int y : G[x]) if(!p[y]) {dfs(y, x); sum=w[y]; mx[rt=0]=1e9; dfs(y, x); dfz(rt); }
}signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);freopen("fn.in", "r", stdin);freopen("fn.out", "w", stdout);
// T=read();
// while(T--) {
//
// }n=read(); m=read(); sq=sqrt(m);
// printf("# %lld\n", sq); for(i=1; i<=n; ++i) a[i]=read(); for(i=1; i<n; ++i) {u=read(); v=read(); G[u].pb(v); G[v].pb(u); }sum=n; mx[rt=0]=1e9; dfs(1, 0); Rt=rt;
// printf("%lld\n", rt); dfz(rt);printf("%lld", (ans%mo+mo)%mo); return 0;
}的方法:UNIX域套接字)






)








)

)
