一、袖珍计算器
袖珍计算器方法主要运用到了我们高数上所学的关于e底数转化的思想,即
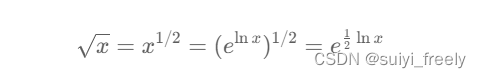
一种用指数函数 exp 和对数函数 ln 代替平方根函数的方法 :
1、exp函数:
exp是 C 标准库 <math.h> 中的一个函数,用于计算 e 的 x 次幂,其中 e 是自然对数的底数(约为 2.71828)。
函数声明:
#include <math.h>double exp(double x);
float expf(float x);
long double expl(long double x);
函数用法:
#include <stdio.h>
#include <math.h>int main ()
{double x = 0;printf("e 的 %lf 次幂是 %lf\n", x, exp(x));printf("e 的 %lf 次幂是 %lf\n", x+1, exp(x+1));printf("e 的 %lf 次幂是 %lf\n", x+2, exp(x+2));return(0);
}2、log函数:
log是 C 标准库 <math.h> 中的一个函数,用于计算一个浮点数的自然对数(以 e 为底)。
函数声明:
#include <math.h>double log(double x);
float logf(float x);
long double logl(long double x);
函数返回值:
- 如果
x为负数,log()函数将返回 NaN,并设置errno为EDOM。 - 如果
x为零,log()函数将返回-HUGE_VAL(负无穷大),并设置errno为ERANGE。
(
C 库宏 extern int errno 是通过系统调用设置的,在错误事件中的某些库函数表明了什么发生了错误。
errno 是 C 标准库中的一个宏,定义在 <errno.h> 头文件中。它用于指示在程序运行过程中发生的错误。errno 实际上是一个整数变量,用于存储错误代码。库函数在发生错误时,会设置 errno 为适当的错误代码,以便程序可以检查和处理这些错误。
)
函数用法:
#include <stdio.h>
#include <math.h>int main ()
{double x, ret;x = 2.7;/* 计算 log(2.7) */ret = log(x);printf("log(%lf) = %lf", x, ret);return(0);
}3、实现
所以我们可以写出如下的函数:
int mySqrt(int x) {if (x == 0) {return 0;}int ans = exp(0.5 * log(x));return ans;}但是在leetcode上提交会有一项通不过:
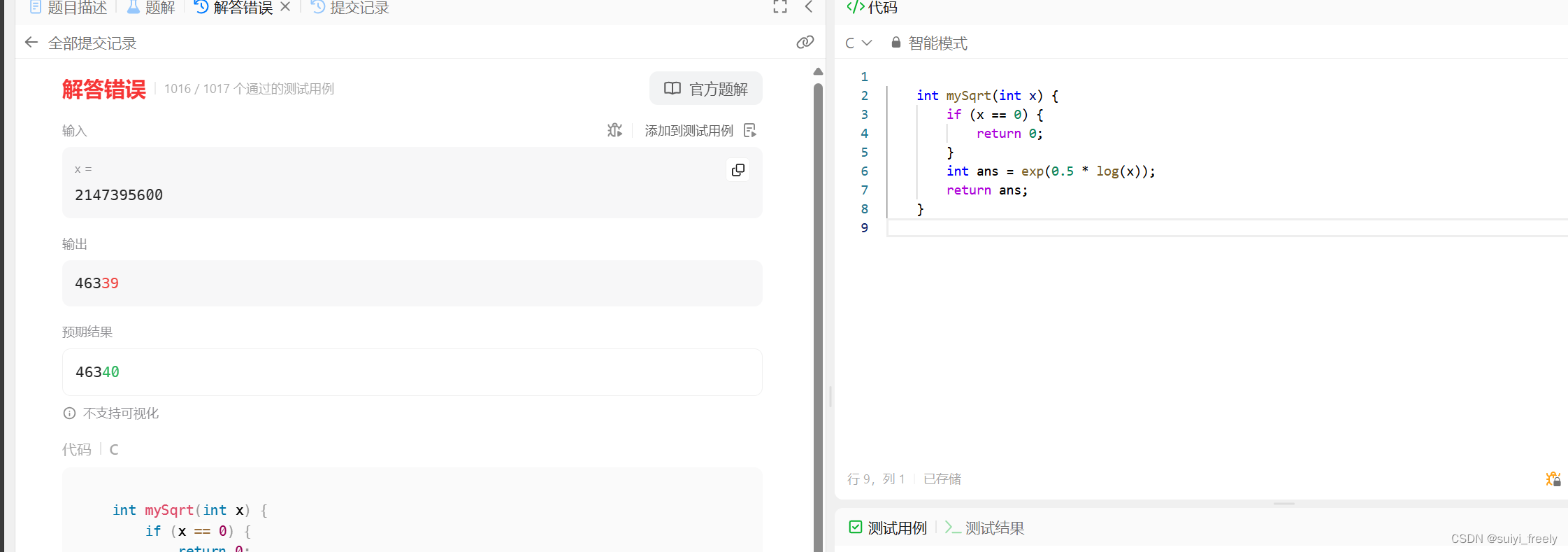
由于计算机无法存储浮点数的精确值,而指数函数和对数函数的参数和返回值均为浮点数,因此运算过程中会存在误差。例如当 x=2147395600的计算结果与正确值 463404634046340 相差 10^-11 ,这样在对结果取整数部分时,会得到 463394633946339 这个错误的结果。因此在得到结果的整数部分后,我们应当再将(ans+1)^2的值再与x经行比较如果比x小则说明出现了刚刚那种情况。
二、二分查找
这种思想主要是来源于对于x的平方根ans(平方根的整数部分)来说:ans^2一定是<=x的,
(ans+1)^2>x
所以一种简单的思想是将从0到x的所有值与x按照上面的思路比较
int mySqrt(int x) {unsigned long long len=0;unsigned long long ret=0;while(len<=x){if(len*len<=x&&(len+1)*(len+1)>x){ret=len;break;}len++;}return ret;}但是实际上我们比较的时候是相当于对有序数组经行查找操作,所以我们可以用二分查找的想法去改进这个题:
int mySqrt(int x)
{int l = 0, r = x, ans = -1;while (l <= r) {long long mid = l + (r - l) / 2;if (mid * mid <= x) {ans = mid;l = mid + 1;}else {r = mid - 1;}}return ans;}三、牛顿迭代
1、原理
牛顿迭代法是一种可以用来快速求解函数零点的方法。(链接:牛顿迭代法_百度百科 (baidu.com))我们可以设出如下函数:
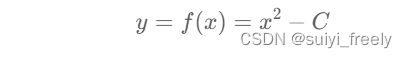
显然:c的平方根计算f(x)的零点(零点是x的值,这里我们取正的);
牛顿迭代法的本质是借助泰勒级数,从初始值开始快速向零点逼近。我们任取一个xo作为初始值,在每一步的迭代中,我们找到函数图像上的点(xi,f(xi)),过该点作一条斜率为该点导数f'(xi)的直线,与横轴的交点记为xi+1。xi+1相较于xi而言距离零点更近。在经过多次迭代后,我们就可以得到一个距离零点非常接近的交点。
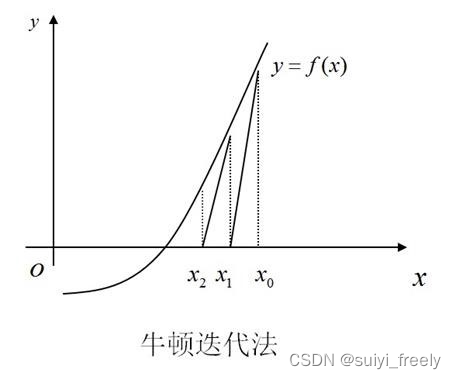
按照我的理解就是利用函数切点斜率等于函数值变化率的 本质使得f(xo)的值快速往下降最终降到为0时即为零点。
2、算法
我们选择xo=C作为初始值。
在每一步迭代中,我们通过当前的交点xi,找到函数图像上的点(xi,x²-C),作一条斜率为f'(xi)=2x;的直线,直线的方程为:
y=2xi*(x-xi)+xi²-C
=2xi*x-(x²+C)
与横轴的交点为方程2xi*x-(xi²+C)=0的解,即为新的迭代结果xi+1=1/2*(xi+c/xi)
在进行k次迭代后,xk的值与真实的零点√C足够接近,即可作为答案。
什么时候结束呢?
一般来说,可以判断相邻两次迭代的结果的差值是否小于一个极小的非负数 ϵ,其中 ϵ 一般可以取 10^−6或 10^-7(再leetcode上这个数据段可以用1e-7来实现也可以看这篇博客:(C中float类型与0比较用e-7的原因_fabs(disc) <= 1e-7-CSDN博客)
3、实现:
class Solution {
public:int mySqrt(int x) {if (x == 0) {return 0;}double C = x, x0 = x;while (true) {double xi = 0.5 * (x0 + C / x0);if (fabs(x0 - xi) < 1e-7) {break;}x0 = xi;}return int(x0);}
};
)













)




ingress+elb部署实践)