
Problem: 209. 长度最小的子数组
文章目录
- 题意分析
- 算法原理讲解
- 暴力枚举O(N^2)
- 利用单调性,滑动窗口求解
- 复杂度
- Code
题意分析
首先来分析一下本题的题目意思
- 题目中会给到一个数组,我们的目的是找出在这个数组中 长度最小的【连续】子数组,而且要返回这个子数组的长度
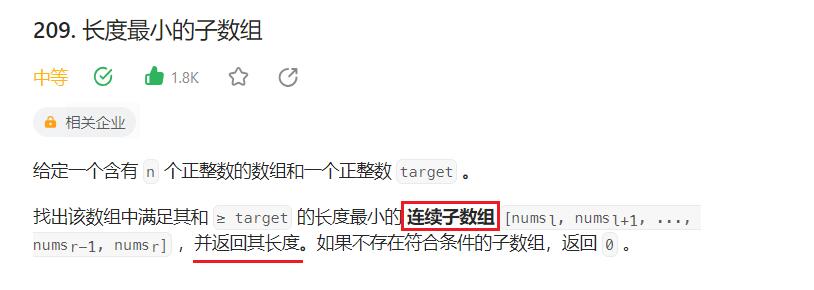
- 那我们首先来看示例1,在所找出的所有连续的子数组后,我们需要去比较谁的长度比较短一些,然后去选择短一些的这个子数组
- 下面们我们看这个示例3,其最后的返回长度为0,原因就在于给出的整型数组中所有数之和还是没有超过
target,所以呢就返回了0

💬 但是要如何去寻找这个最小的子数组呢,我们马上来揭晓🖐
算法原理讲解
我们通过分析此题的算法原理来看看该如何去进行求解
暴力枚举O(N^2)
首先第一种,还是我们最熟悉的暴力解法
- 不过也是要使用到双指针的,我们从0的位置开始向后遍历
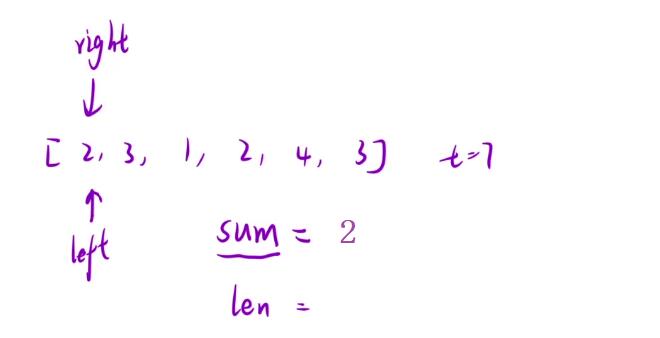

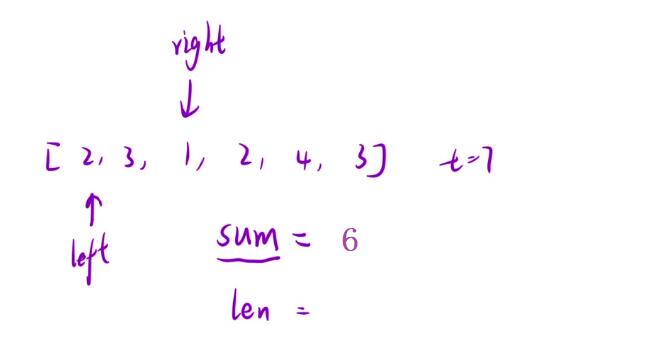
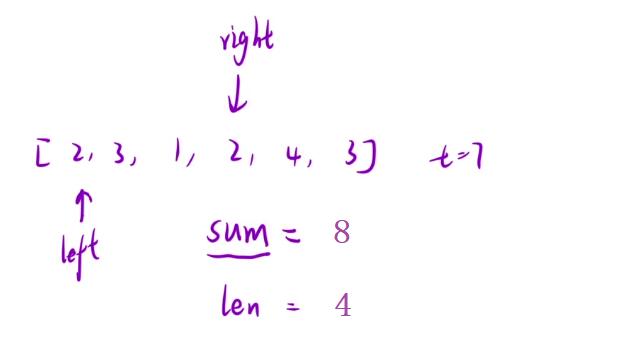
- 好,通过上面的这个图示,我们可以清晰地看出经过
right的不断后移中,我们发现了一组长度> target的数据。但是呢我们这里使用的是【暴力枚举】,所以此时还会继续向后进行遍历操作→
可以观察到,当这个right继续后移将所遍历到的数加到sum上去的时候,虽然sum的大小是比target来得大了,但是呢这个len 的长度也相对应地发生可增长,这个其实的话就不对了,因为题目中所要求我们的是求解 最小子数组的长度
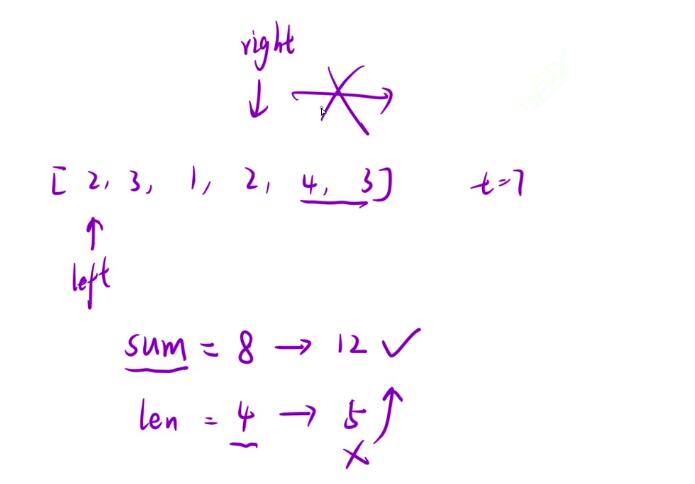
利用单调性,滑动窗口求解
看了上面的部分思路后,确实觉得暴力解法不可行,所以我接下去会使用【滑动窗口】的思想去做一个优化的操作
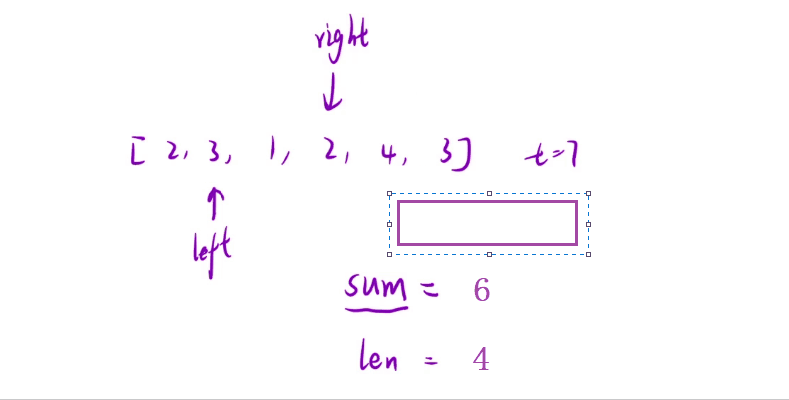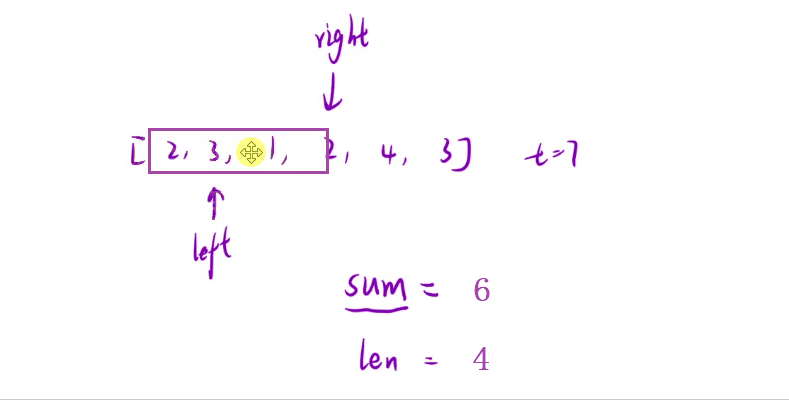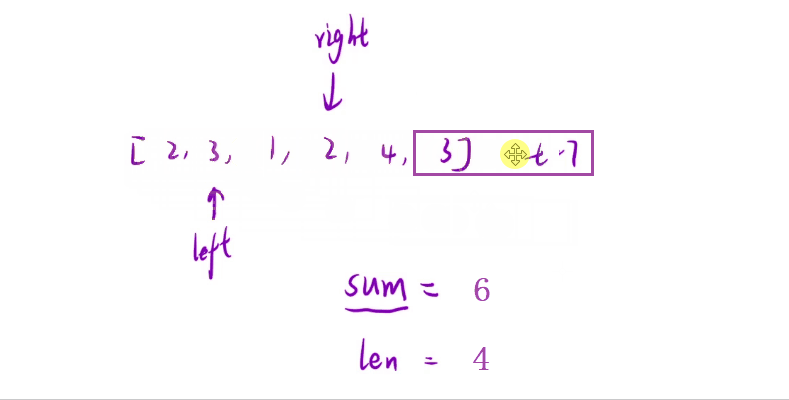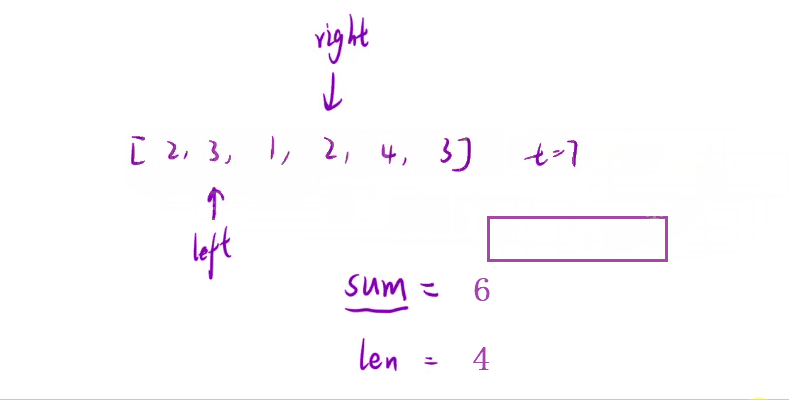
- 我们可以将
left向后移动一位,此时子数组的和即为当前的sum减去left刚刚所指位置的那个数,即为【6】,那么我们在计算整个子数组的和时就可以不用让right重新开始遍历计算

💬 对于上面的这种 “同向移动的指针” 我们就称之为【滑动窗口】,读者可以看看下面的这个动图
那接下去呢我就来叙述一下如何使用【滑动窗口】的思想
- 令
left = 0, right = 0 - 数据进窗口
- 判断当前数据是否超过了目标值
target- 更新结果,数据出窗口
- 继续循环往复
- 读者可以通过看下面的算法流程图,让后配合后面的代码,来思考这个滑动窗口的奇妙之处
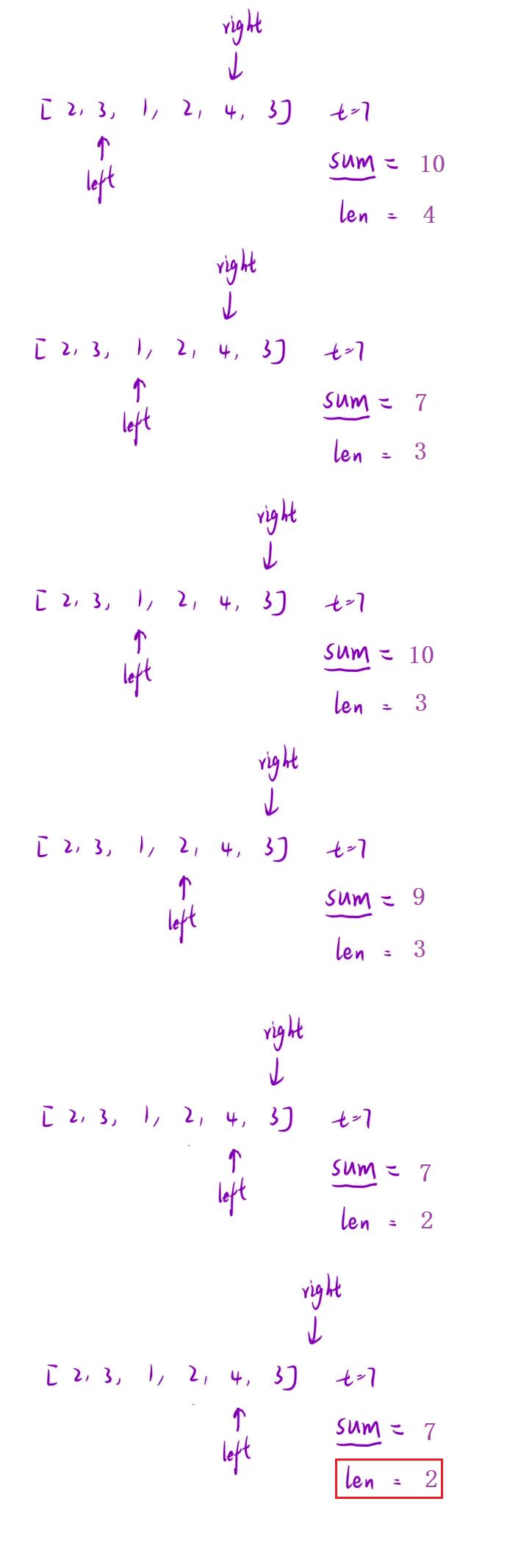
💬 那有读者一定会问了,怎么能保证这个滑动窗口一定是正确的呢?
- 虽然在这里我们并没有像暴力枚举那样列出的可能性然后再去比较,但是呢我们可以知道接下来的情况枚举了也是白枚举,所以呢我们利用【单调性】,规避了很多没有必要的枚举行为
复杂度
- 时间复杂度:
对于时间复杂度, 等会读者在看代码的时候可以看到是存在两个嵌套的循环,所以就自认为是 O ( n 2 ) O(n^2) O(n2),但是呢这里的时间复杂度应该是 O ( n ) O(n) O(n)才对
- 我们通过看下面的这张图来理解一下,
left和right指针在移动的时候都是一步步走的,当最后right指针移动到末尾结束的时候,我们考虑最坏的情况,就是两个指针分别都遍历了一遍这个数组, 2 O ( n ) 2O(n) 2O(n)时间复杂度即为 O ( n ) O(n) O(n)

- 空间复杂度:
没有开出任何多余的空间,那么空间复杂度即为 O ( n ) O(n) O(n)
Code
以下即为滑动窗口的代码
- 注意最后在返回的时候要判断这个
len是否有做更新,如果还是为最初的INT_MAX的话就不对了
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int n = nums.size();int sum = 0;int len = INT_MAX;for(int left = 0, right = 0; right < n; ++right) {sum += nums[right]; // 进窗口while(sum >= target){len = min(len, right - left + 1); // 更新最短长度sum -= nums[left++]; // 出窗口}}return len == INT_MAX ? 0 : len;}
};












)







