word效果预览:


一、我会填
1. 1.\hspace{0.5em} 1. 一个多位数,亿位上是次小的素数,千位上是最小的质数的立方,十万位是 10 10 10 和 15 15 15 的最大公约数,万位是最小的合数,十位上的数既不是质数也不是合数,这个数是 ( \hspace{4em} ),约等于 ( \hspace{1em} ) 万
2. 2.\hspace{0.5em} 2. 9 : ( ) = ( ) 64 = 18.75 % = ( ) ( 填小数 ) 9:(\hspace{1em})=\frac{(\hspace{1em})}{64}=18.75\%=(\hspace{1.5em})(填小数) 9:()=64()=18.75%=()(填小数)
3. 3.\hspace{0.5em} 3. 小明有一个 3 3 3m 长的竹竿,如果平均切 5 5 5 下,那么每一段占全长的 ( \frac{\hspace{1em}}{} ),每一段是 ( \hspace{1em} ) dm。
4. 4.\hspace{0.5em} 4. 在一幅比例尺为 1 : 1000000 1:1000000 1:1000000 的地图上,小刚家到他姥姥家,地图上为 12 12 12cm,如果平均车速为 2.5 2.5 2.5km/min,那么需要 ( \hspace{1em} ) 秒 才能到达姥姥家。
5. 5.\hspace{0.5em} 5. 23000 23000 23000平方米=( \hspace{1em} ) 公顷 4 \hspace{3em}4 4t 250 250 250g= ( \hspace{1em} ) kg
6. 6.\hspace{0.5em} 6. 6年级3班有 40 40 40 名同学,占六年级学生总数的 2 11 \frac{2}{11} 112,六年级学生总数又占全校的 4 25 \frac{4}{25} 254,那么全校有 ( \hspace{1em} ) 名同学。
7. 7.\hspace{0.5em} 7. 有 241 241 241 个苹果,如果有 4 4 4 个篮子,至少有一个篮子有 ( \hspace{1em} ) 个苹果。
8. 8.\hspace{0.5em} 8. 如果 + 3 3 3 表示多了 3 3 3 个苹果,那么可以用 ( \hspace{1em} ) 来表示少了 7 7 7 个苹果。
9. 9.\hspace{0.5em} 9. 如果 y = 12 7 x y=\frac{12}{7}x y=712x,那么 y : x = y:x= y:x= ( \hspace{2em} )。
10. 10.\hspace{0.5em} 10. 一个圆柱切成了 5 5 5 段,表面积增加了 226.08 d m 2 226.08dm^2 226.08dm2,每个小圆柱的高都是 3 3 3m,那么把这个圆柱削成一个等底等高的圆锥,圆锥的体积是 ( \hspace{1.5em} ) ( π \pi π按3.14算)。
11. 11.\hspace{0.5em} 11. 有 x x x 个点的图上,最多可以连 ( \hspace{1em} ) 条线段。
12. 12.\hspace{0.5em} 12. 一套衣服 65 65 65 元,A 商场打九折,B 商场满 10 10 10 元减 1 1 1 元,在 ( \hspace{1em} ) 更划算。
二、用心思考,慎重选择
1. 1.\space 1. 有一个比为 3 : 4 3:4 3:4,如果前项增加 21 21 21,那么后项应( \hspace{1em} )。
\hspace{2em} A. 加 21 21 21 \hspace{1em} B.乘 7 7 7 \hspace{1em} C.加 28 28 28 \hspace{1em} D.以上答案都不对
2. 2.\space 2. 一个圆的半径增加了50%,那么它的面积增加了 ( \hspace{1em} )。
\hspace{2em} A. 50% \hspace{2em} B. 75% \hspace{2em} C. 100% \hspace{2em} D. 125%
3. 3.\space 3. 一个正方体的体积是125立方厘米,它的表面积是 ( \hspace{1em} )平方厘米。
\hspace{2em} A. 150 \hspace{2em} B. 125 \hspace{2em} C. 200 \hspace{2em} D. 25
4. 4.\space 4. 如果一个矩形的周长是18厘米,它的长是5厘米,那么它的宽是 ( \hspace{1em} )厘米。
\hspace{2em} A. 3 \hspace{2em} B. 4 \hspace{2em} C. 5 \hspace{2em} D. 6
5. 5.\space 5. 在一个等边三角形ABC中,AB的长度为 10 10 10cm,点D在边AC上,且AD的长度为 4 4 4cm,那么DC的长度是( \hspace{1em} )。
A.6cm \hspace{2em} B. 10cm \hspace{2em} C. 4cm \hspace{2em} D.5cm
6. 6.\space 6. 一个圆柱的底面半径为10cm,它的体积是一个圆锥的体积的2倍,高是 4.5 4.5 4.5cm,那么这个圆锥的底面半径是( \hspace{1em} )。
\hspace{2em} A. 11cm \hspace{2em} B. 10 3 \frac{10}{3} 310cm \hspace{2em} C. 10cm \hspace{2em} D. 5cm
7. 7.\space 7. 在动画片中,喜羊羊在 1 1 1 分钟内使用超负荷进行投球,二分球与三分球的比是 5 : 2 5:2 5:2,如果喜羊羊得了 32 32 32 分,那么二分球的数量比三分球的数量多( \hspace{1em} )。
A. 150% \hspace{2em} B.170% \hspace{2em} C. 50% \hspace{2em} D.250%
8. 8.\space 8. 如图,中间的小正方形的面积是( \hspace{1em} ) c m 2 cm^2 cm2。
A.16 \hspace{2em} B.15 \hspace{2em} C 4.5 \hspace{2em} D.10
9. 9.\space 9. 7:x=13:26,那么x=( \hspace{1em} )。
\hspace{2em} A.26 \hspace{2em} B.14 \hspace{2em} C.7 \hspace{2em} D.13
10. 10.\space 10. 一个虫子,一分钟之后会分裂成 2 2 2 个,二分钟后会变成 4 4 4 个,以此类推。第 20 20 20 分钟会有( \hspace{1em} )个虫子。
\hspace{3em} A.1048576 \hspace{1em} B.1048578 \hspace{1em} C.2097152 \hspace{1em} D.514288
三、计算题
1. 1. 1. 直接写得数
2 3 + 1 2 = \frac{2}{3} + \frac{1}{2}=\hspace{2em} 32+21= 5 6 − 1 3 = \frac{5}{6} - \frac{1}{3}=\hspace{2em} 65−31= 3 4 × 2 3 = \frac{3}{4} \times \frac{2}{3}=\hspace{2em} 43×32= 4 5 ÷ 2 3 = \frac{4}{5} \div \frac{2}{3}=\hspace{2em} 54÷32=
1 ÷ 25 % = 125 × 1 8 = 24 × ( 1 2 + 3 1 ) = 1\div25\%=\hspace{2em}125\times\frac{1}{8}=\hspace{2em}24\times(\frac{1}{2}+\frac{3}{1})=\hspace{2em} 1÷25%=125×81=24×(21+13)=
25 × 32 × 125 = 81 ÷ 9 5 = 639 ÷ 67 ≈ 25\times32\times125=\hspace{2em81\div\frac{9}{5}}=\hspace{2em} 639\div67\approx 25×32×125=81÷59=639÷67≈
398 × 46 ≈ 4 9 × 5 9 × 81 = 398\times46\approx\hspace{4em}\frac{4}{9}\times\frac{5}{9}\times81= 398×46≈94×95×81=
2. 2. 2. 脱式计算(能简算的要简算)
98.6 − 30.7 + 12.4 − 25.3 2 5 × 3 4 + 2 5 ÷ 4 \hspace{1em}98.6-30.7+12.4-25.3\hspace{3em}\frac{2}{5}\times\frac{3}{4}+\frac{2}{5}\div4 98.6−30.7+12.4−25.352×43+52÷4
\hspace{1em}
\hspace{1em}
\hspace{1em}
12.5 × 25 × 0.08 × 0.4 2024 × 2022 2023 \hspace{1em}12.5\times25\times0.08\times0.4\hspace{4.3em}2024\times\frac{2022}{2023} 12.5×25×0.08×0.42024×20232022
\hspace{1em}
\hspace{1em}
\hspace{1em}
272 ÷ 16 + 204 × 6 ( 4 7 + 5 8 − 6 28 ) × 112 \hspace{1em}272\div16+204\times6\hspace{4em}(\frac{4}{7}+\frac{5}{8}-\frac{6}{28})\times112 272÷16+204×6(74+85−286)×112
\hspace{1em}
\hspace{1em}
\hspace{1em}
3. 3. 3. 解方程
( x − 3 ) : ( 3 x + 7 ) = 1 : 7 7 ÷ 4 x = 21 8 \hspace{2em}(x-3):(3x+7)=1:7\hspace{4em}7\div4x=\frac{21}{8} (x−3):(3x+7)=1:77÷4x=821
\hspace{1em}
\hspace{1em}
\hspace{1em}
四、操作题
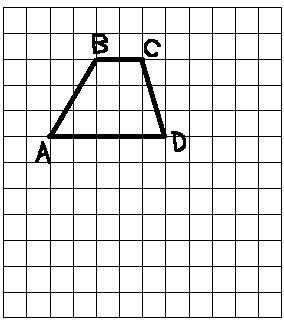
1. 1. 1. A点的位置在( \hspace{1em} , \hspace{0.8em} ).
2. 2. 2. 请画出梯形ABCD绕D点转 90°后的图形,然后画出旋转后图形向右平移 4 4 4 格后的图形。
3. 3. 3. 按1:2 画出缩小后的图形,缩小后的图形是 ( \hspace{1em} )平方厘米。(一格为 4 4 4 cm 2 ^2 2)。
五、解决问题
1. 1. 1. 小明第一天读了 72 72 72 页数,第二天读的是第一天的 5 8 \frac{5}{8} 85,这是,已读页数和未读页数的比是 1 : 4 1:4 1:4,那么这本书总共多少页?
\hspace{1em}
\hspace{1em}
\hspace{1em}
\hspace{1em}
2. 2. 2. 一项工程,如果 25 25 25 天完成,每天需要做 40 40 40 个,如果要提前 5 5 5 天完成,需要多少时间?(用比例解)
\hspace{1em}
\hspace{1em}
\hspace{1em}
\hspace{1em}
3. 3. 3. 有一个水瓶,小明喝了一部分之后,水的高度占瓶子的高度的 5 7 \frac{5}{7} 75,如果将瓶子倒置之后,有水部分占瓶子高度的 6 7 \frac{6}{7} 76,已知瓶子高度为 28 28 28,底面半径为 4 4 4,那么瓶子里还有多少水?
\hspace{1em}
\hspace{1em}
\hspace{1em}
\hspace{1em}
4. 4. 4. 有一个圆锥形沙堆的半径为 4 c m 4cm 4cm,高为 8.4 c m 8.4cm 8.4cm,如果铺在一个半径为 2 2 2 的圆柱形容器内,能铺多少 cm?
\hspace{1em}
\hspace{1em}
\hspace{1em}
\hspace{1em}
5. 5. 5. 在一幅比例尺是 1 : 2500000 1:2500000 1:2500000 的地图上,地点甲到乙的距离是 15 c m 15cm 15cm,有一个客车和一个货车相向而行, 3 3 3 小时相遇,已知客车和货车的速度比是 2 : 3 2:3 2:3,那么客车的时速是多少?货车的时速是多少?
\hspace{1em}
\hspace{1em}
\hspace{1em}
\hspace{1em}
6. 6. 6. 在一个时间一个地点,小明是 1.8 1.8 1.8m,他的影子是 4 m 4m 4m,如果一棵树的影子长 240m,那么这棵树有多高?(用比例解)
\hspace{1em}
\hspace{1em}
\hspace{1em}
\hspace{1em}
数学加油站

文件在这:链接:https://pan.baidu.com/s/1ZKWq_FIJ0O9LR-6HM2Noww?pwd=pziv
提取码:pziv
源码尽管拿
**一、我会填**
$1.\hspace{0.5em}$ 一个多位数,亿位上是次小的素数,千位上是最小的质数的立方,十万位是 $10$ 和 $15$ 的最大公约数,万位是最小的合数,十位上的数既不是质数也不是合数,这个数是 ($\hspace{4em}$),约等于 ($\hspace{1em}$) 万
$2.\hspace{0.5em}$ $9:(\hspace{1em})=\frac{(\hspace{1em})}{64}=18.75\%=(\hspace{1.5em})(填小数)$
$3.\hspace{0.5em}$ 小明有一个 $3$m 长的竹竿,如果平均切 $5$ 下,那么每一段占全长的 ($\frac{\hspace{1em}}{}$),每一段是 ($\hspace{1em}$) dm。
$4.\hspace{0.5em}$ 在一幅比例尺为 $1:1000000$ 的地图上,小刚家到他姥姥家,地图上为 $12$cm,如果平均车速为 $2.5$km/min,那么需要 ($\hspace{1em}$) 秒 才能到达姥姥家。
$5.\hspace{0.5em}$ $23000$平方米=($\hspace{1em}$) 公顷$\hspace{3em}4$t $250$g= ($\hspace{1em}$) kg
$6.\hspace{0.5em}$ 6年级3班有$40$ 名同学,占六年级学生总数的 $\frac{2}{11}$,六年级学生总数又占全校的 $\frac{4}{25}$,那么全校有 ($\hspace{1em}$) 名同学。
$7.\hspace{0.5em}$ 有 $241$ 个苹果,如果有 $4$ 个篮子,至少有一个篮子有 ($\hspace{1em}$) 个苹果。
$8.\hspace{0.5em}$ 如果 +$3$ 表示多了 $3$ 个苹果,那么可以用 ($\hspace{1em}$) 来表示少了 $7$ 个苹果。
$9.\hspace{0.5em}$ 如果 $y=\frac{12}{7}x$,那么 $y:x=$ ($\hspace{2em}$)。
$10.\hspace{0.5em}$ 一个圆柱切成了 $5$ 段,表面积增加了 $226.08dm^2$,每个小圆柱的高都是 $3$m,那么把这个圆柱削成一个等底等高的圆锥,圆锥的体积是 ($\hspace{1.5em}$) ($\pi$按3.14算)。
$11.\hspace{0.5em}$ 有 $x$ 个点的图上,最多可以连 ($\hspace{1em}$) 条线段。
$12.\hspace{0.5em}$ 一套衣服 $65$ 元,A 商场打九折,B 商场满 $10$ 元减 $1$ 元,在 ($\hspace{1em}$) 更划算。
**二、用心思考,慎重选择**$1.\space$ 有一个比为 $3:4$,如果前项增加 $21$,那么后项应($\hspace{1em}$)。$\hspace{2em}$A. 加 $21$$\hspace{1em}$B.乘 $7$ $\hspace{1em}$C.加 $28$ $\hspace{1em}$D.以上答案都不对$2.\space$ 一个圆的半径增加了50%,那么它的面积增加了 ($\hspace{1em}$)。$\hspace{2em}$ A. 50% $\hspace{2em}$B. 75%$\hspace{2em}$ C. 100%$\hspace{2em}$ D. 125%$3.\space$ 一个正方体的体积是125立方厘米,它的表面积是 ($\hspace{1em}$)平方厘米。
$\hspace{2em}$ A. 150 $\hspace{2em}$B. 125 $\hspace{2em}$C. 200$\hspace{2em}$ D. 25$4.\space$ 如果一个矩形的周长是18厘米,它的长是5厘米,那么它的宽是 ($\hspace{1em}$)厘米。
$\hspace{2em}$ A. 3 $\hspace{2em}$B. 4 $\hspace{2em}$C. 5 $\hspace{2em}$D. 6$5.\space$在一个等边三角形ABC中,AB的长度为$10$cm,点D在边AC上,且AD的长度为$4$cm,那么DC的长度是($\hspace{1em}$)。A.6cm $\hspace{2em}$B. 10cm $\hspace{2em}$C. 4cm $\hspace{2em}$D.5cm $6.\space$一个圆柱的底面半径为10cm,它的体积是一个圆锥的体积的2倍,高是$4.5$cm,那么这个圆锥的底面半径是($\hspace{1em}$)。
$\hspace{2em}$ A. 11cm $\hspace{2em}$B. $\frac{10}{3}$cm $\hspace{2em}$C. 10cm $\hspace{2em}$D. 5cm$7.\space$在动画片中,喜羊羊在 $1$ 分钟内使用超负荷进行投球,二分球与三分球的比是 $5:2$,如果喜羊羊得了 $32$ 分,那么二分球的数量比三分球的数量多($\hspace{1em}$)。A. 150% $\hspace{2em}$B.170%$\hspace{2em}$ C. 50% $\hspace{2em}$D.250%$8.\space$如图,中间的小正方形的面积是($\hspace{1em}$)$cm^2$。
A.16$\hspace{2em}$ B.15$\hspace{2em}$ C 4.5 $\hspace{2em}$D.10$9.\space$ 7:x=13:26,那么x=($\hspace{1em}$)。$\hspace{2em}$A.26 $\hspace{2em}$B.14 $\hspace{2em}$C.7 $\hspace{2em}$D.13$10.\space$ 一个虫子,一分钟之后会分裂成 $2$ 个,二分钟后会变成 $4$ 个,以此类推。第 $20$ 分钟会有($\hspace{1em}$)个虫子。$\hspace{3em}$A.1048576 $\hspace{1em}$B.1048578$\hspace{1em}$ C.2097152 $\hspace{1em}$D.514288
**三、计算题**
$1.$ 直接写得数
$\frac{2}{3} + \frac{1}{2}=\hspace{2em}$$\frac{5}{6} - \frac{1}{3}=\hspace{2em}$$\frac{3}{4} \times \frac{2}{3}=\hspace{2em}$$\frac{4}{5} \div \frac{2}{3}=\hspace{2em}$$1\div25\%=\hspace{2em}125\times\frac{1}{8}=\hspace{2em}24\times(\frac{1}{2}+\frac{3}{1})=\hspace{2em}$$25\times32\times125=\hspace{2em81\div\frac{9}{5}}=\hspace{2em} 639\div67\approx$$398\times46\approx\hspace{4em}\frac{4}{9}\times\frac{5}{9}\times81=$
$2.$ 脱式计算(能简算的要简算)
$\hspace{1em}98.6-30.7+12.4-25.3\hspace{3em}\frac{2}{5}\times\frac{3}{4}+\frac{2}{5}\div4$
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$$\hspace{1em}12.5\times25\times0.08\times0.4\hspace{4.3em}2024\times\frac{2022}{2023}$
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$$\hspace{1em}272\div16+204\times6\hspace{4em}(\frac{4}{7}+\frac{5}{8}-\frac{6}{28})\times112$
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$$3.$ 解方程
$\hspace{2em}(x-3):(3x+7)=1:7\hspace{4em}7\div4x=\frac{21}{8}$
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$**四、操作题**

$1.$ A点的位置在( $\hspace{1em}$,$\hspace{0.8em}$).
$2.$ 请画出梯形ABCD绕D点转 90°后的图形,然后画出旋转后图形向右平移 $4$ 格后的图形。
$3.$ 按1:2 画出缩小后的图形,缩小后的图形是 ($\hspace{1em}$)平方厘米。(一格为$4$ cm$^2$)。
五、解决问题
$1.$ 小明第一天读了 $72$ 页数,第二天读的是第一天的 $\frac{5}{8}$,这是,已读页数和未读页数的比是 $1:4$,那么这本书总共多少页?
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
$2.$ 一项工程,如果 $25$ 天完成,每天需要做 $40$ 个,如果要提前 $5$ 天完成,需要多少时间?(用比例解)
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
$3.$ 有一个水瓶,小明喝了一部分之后,水的高度占瓶子的高度的 $\frac{5}{7}$,如果将瓶子倒置之后,有水部分占瓶子高度的 $\frac{6}{7}$,已知瓶子高度为 $28$,底面半径为 $4$,那么瓶子里还有多少水?
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
$4.$ 有一个圆锥形沙堆的半径为 $4cm$,高为 $8.4cm$,如果铺在一个半径为 $2$ 的圆柱形容器内,能铺多少 cm?
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
$5.$ 在一幅比例尺是 $1:2500000$ 的地图上,地点甲到乙的距离是 $15cm$,有一个客车和一个货车相向而行, $3$ 小时相遇,已知客车和货车的速度比是 $2:3$,那么客车的时速是多少?货车的时速是多少?
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
$6.$ 在一个时间一个地点,小明是 $1.8$m,他的影子是 $4m$,如果一棵树的影子长 240m,那么这棵树有多高?(用比例解)
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
$\hspace{1em}$
**数学加油站**












低通滤波反相放大器电路和积分器电路)
)


)
)

