介绍
这篇论文提出了一种新型的"选择性状态空间模型"(Selective State Space Model, S6)来解决之前结构化状态空间模型(SSM)在离散且信息密集的数据(如文本)上效果较差的问题。
Mamba 在语言处理、基因组学和音频分析等领域的应用中表现出色。其创新的模型采用了线性时间序列建模架构,结合了选择性状态空间,能够在语言、音频和基因组学等不同模式中提供卓越的性能。这种突破性的模型标志着机器学习方法的重大转变,显著提升了效率和性能。Mamba 的主要优势之一是能够解决传统 Transformer 在处理长序列时的计算挑战。通过将选择机制集成到其状态空间模型中,Mamba 可以根据序列中每个 token 的相关性,灵活地决定是传播还是丢弃信息。这种选择性的方法显著加快了推理速度,使吞吐率比标准 Transformer 高出五倍,并实现了随序列长度线性扩展。值得注意的是,即使序列扩展到一百万个元素,Mamba 的性能也会随着实际数据的增加而不断提升。
为什么作SSM
基础模型的优缺点
RNN优点
推理很快
RNN缺点
线性空间占用,串行导致龟速的训练过程,但能够进行自然且快速地执行推理
训练过程的梯度反向传播被迫逐个通过各个单元,更新参数
推理过程不需要受这一问题影响,因此RNN受益于其较为简单的结构设计,获得了相对快的推理速度
遗忘问题,无法有效处理长程依赖关系――即便有了LSTM和GRJ等门控的设计,也只是延缓遗忘造成严重影响的位置。
面对长序列仍然无能为力
CNN优点
≥线性空间占用,可以并行训练
CNN缺点
其结构主要关注局部特征,容易忽视全局特征
卷积核主要关注当前元素附近的其他元素,不能直接使当前元素关注长程的其他元素>没有推理方面的优化,固定的卷积核限制了推理速度
相比于RNN,需要额外用卷积核去乘&加多个元素,其推理速度相对平庸
Transformer优点
长距离依赖关系
并行训练
Transformer缺点
计算量大
推理速度慢
Attention优点
可以并行训练,并且可以良好地捕捉长程依赖关系过大的空间复杂度和时间复杂度O(L^2)
Attention缺点
复杂的注意力分数计算过程造成其推理速度缓慢
什么是SSM模型?
状态空间模型”(State Space Model),它是一种用于描述动态系统的数学模型。SSM模型广泛应用于信号处理、控制系统、经济学、金融学等领域,用于建模和预测时间序列数据。
状态空间模型通过两个方程来描述动态系统的演化:
状态方程(**State Equation):描述系统的内部状态如何随时间变化。
观测方程(Observation Equation):描述如何通过观测到的变量(数据)来获取系统的内部状态信息。
公式表示
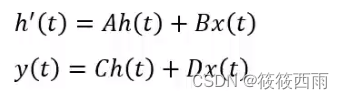
连续函数化,零阶表示
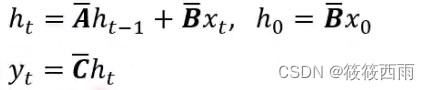
卷积与递归双重属性
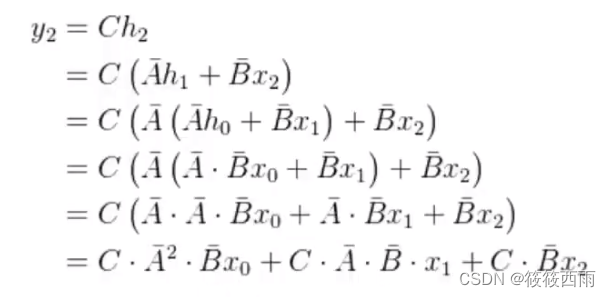
SSM模型到S4模型
SSM模型存在的问题
CNN和RNN的长期依赖捕捉能力都不行,这导致SSM也有这个问题
解决方案
HIPPo矩阵替代随机初始化的A矩阵
A矩阵包含着各个时间步隐状态变化的信息,A矩阵左右着信息遗忘过程使用HIPPO矩阵替换矩阵

相比于随机初始化一个A,使用HIPPO可以有效缓解遗忘问题
为了避免HIPPO本身N2的尺寸带来的过大运算量,利用矩阵分解,使用低秩矩阵表示HIPPO
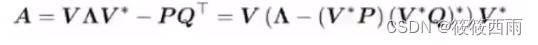
如果想深入了解有关如何计算HiPPO矩阵和自己构建S4模型:可以查看s4的官方文档。
s4注释文档
hippo原文:点击此处
S4模型
序列的结构状态空间,一种可以有效建模长时序依赖的SSM模型
从s4模型到s6模型
1. S4与SSM的问题
ABC矩阵,尤其是最重要的A,只可能在训练过程中更新
自己。一旦训练完成,无论新的输入是什么,都会通过完全一样的A,这导致无法根据输入做针对性推理――无选择性
2.如果使ABC会根据输入变化后的问题:
无法将SSM转化为标准卷积过程
ABC如果能够根据输入的变化而变化,则可以避免这种无选择性
A矩阵和B矩阵参数化后的公式递推:无法预计算卷积核,因为不能做到反向传
播前的训练的过程保持卷积核的不变

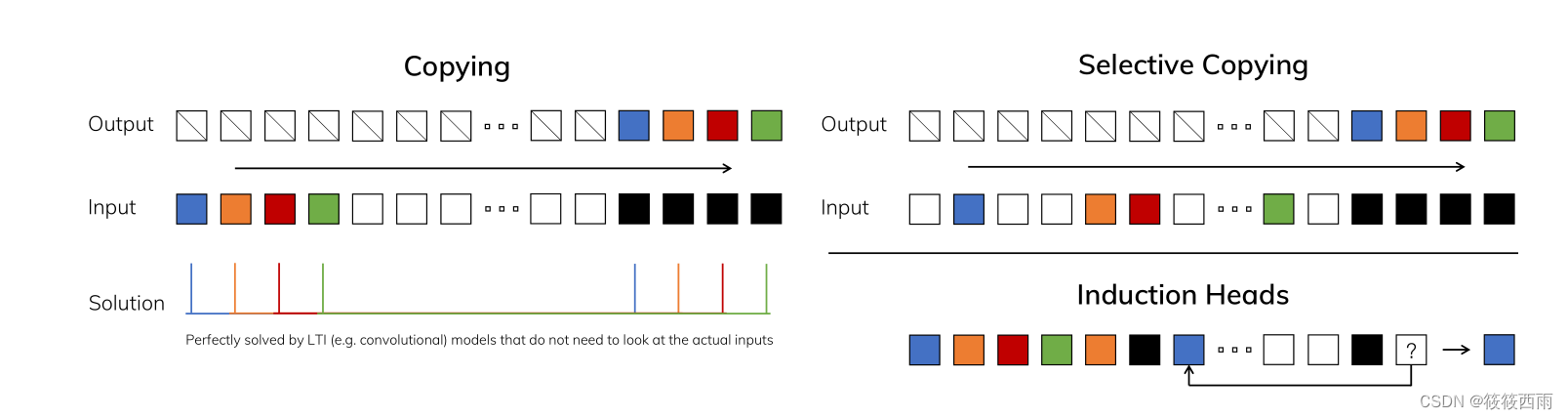
以上详细内容可以参考mamba框架,方便进一步理解。
mamba的具体创新
1. 引入选择机制(Selection Mechanism):
论文发现之前的标准SSM模型缺乏有效地根据输入选择性地处理信息的能力,这限制了它们在离散数据建模上的表现。
作者提出了一种简单但关键的改进,就是让SSM的参数(A, B, C)依赖于当前输入x,从而赋予模型动态选择和过滤信息的能力。
2. 硬件感知的高效算法:
上述选择机制带来了计算效率的挑战,因为标准SSM依赖于时间不变性来实现高效的卷积计算。
作者设计了一种基于扫描(scan)的硬件感知算法,在不损失计算效率的情况下解决了这一问题。
3.简单而统一的架构设计:
作者将选择性SSM与Transformer中的MLP块结合,设计出了一种名为Mamba的新型序列建模架构。
Mamba去除了Transformer中的注意力机制和MLP层,具有更简单和统一的结构。
4. 强大的泛化性能:
实验结果显示,Mamba在合成任务、音频建模、基因组建模以及语言建模等多个领域都取得了出色的表现。
特别是在语言建模上,Mamba-3B的性能可以与Transformer两倍大小的模型媲美。
选择机制

BC变为输入数据驱动的矩阵,尺寸为[BLN]
△变为输入数据驱动的矩阵,尺寸为[BLD]
\overset{-}{A}, \overset{-}{B}最终变成“针对batch内每一条数据的每个时间步,都有对应矩阵”
由于在先前的离散化处理过程中,最终得到的\overset{-}{A}, \overset{-}{B}有△参与,因此最终运算得到的\overset{-}{A}, \overset{-}{B}变成了数据驱动、
不直接把AB参数化成[BLDN]的尺寸,一方面,会造成参数量增大;另一方面,通过上文推导的带有A项的运算,因此只需要参数化成如上的尺寸即可实现AB的参数化
硬件感知算法
该算法使用扫描而不是卷积来循环计算模型,但不实现扩展状态,以避免在GPU内存层次结构的不同级别之间进行IO访问。由此产生的实现在理论上(序列长度线性缩放,与所有基于卷积的ssm的伪线性相比)和现代硬件上(在A100 gpu上快3倍)都比以前的方法快。
并行化――选择性扫描算法(selective scan algorithm)
放弃用卷积来描述SSM,而是定义了一种新的“加”运算,在并行计算中,“连加”操作是可并行的:
假设运算操作的顺序与关联矩阵A无关,会发现每个x乘的矩阵都是源于x本身的(矩阵BC是x通过线性层得到的)
定义新的运算过程
该运算符满足交换律&结合律,取该运算符的第二项结果。虽然不是卷积运算,但是一种并行运算

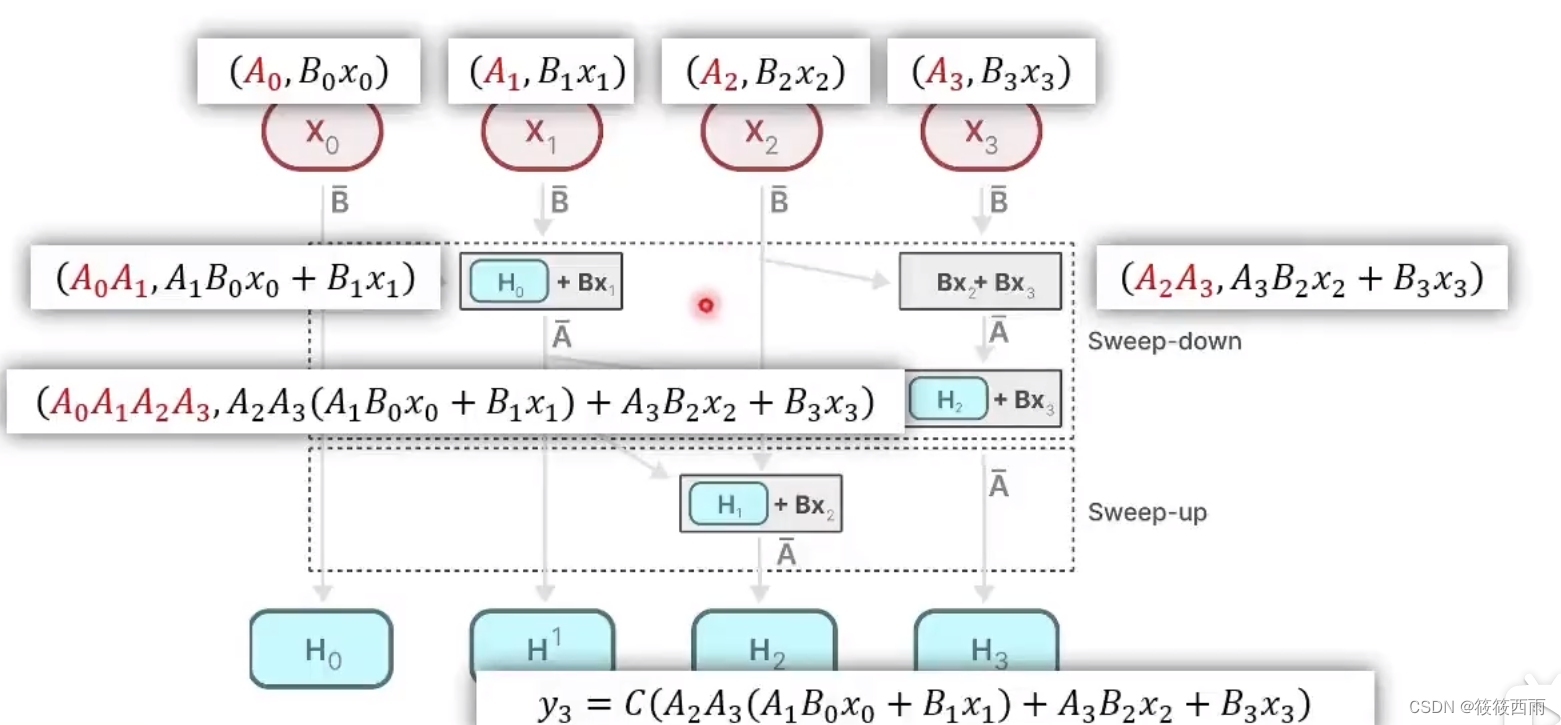
利用SSM本身显存占用小的优势,争取模型和运算过程全部放在SRAM完成;相比之下,Transformer显存占用过大,无法完成这种事情
HBM:显卡的高带宽内存,提供了比传统的GDDR更高的带宽,更低的功耗。当然,相比于SRAM,HBM仍是“低速大容量”的
SRAM:显卡的高速缓存区,读取速度非常快
Transformer仅注意力层可能就需要把模型各个模块分批次从HBM加载到SRAM去计算,一个模块算完了就从SRAM取出来,再加载下一个模块,如,先算QKv,再算注意力分数,注意力分数再与输入相乘
SsM的参数(原始的A,B,C,4会被直接加载到SRAM,在SRAM里计算A,B及后续操作,一步直接得到输出,从SRAM写回HBM)
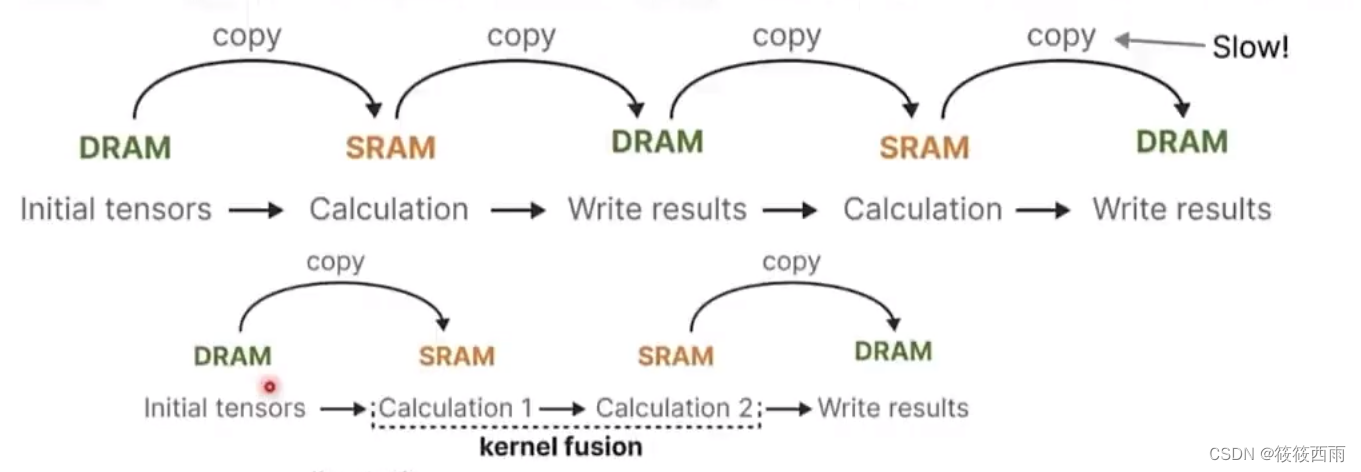
简单而统一的架构设计
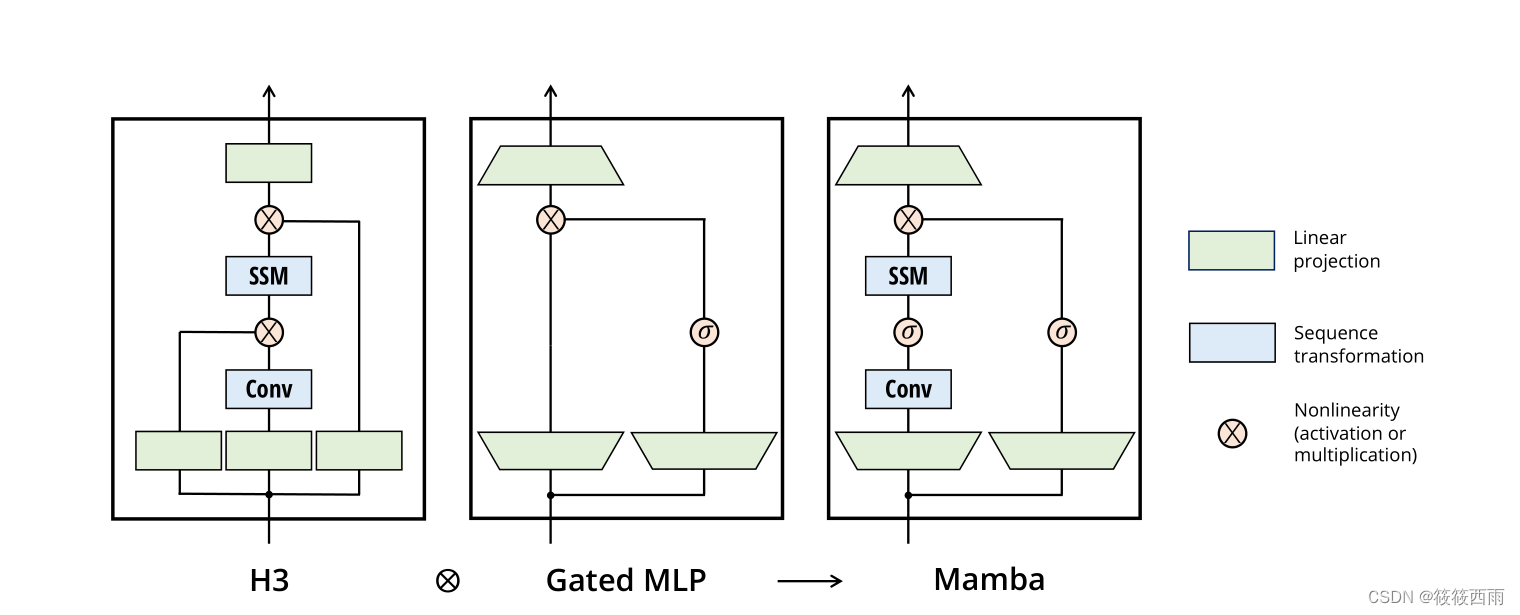
- 去除Transformer的注意力机制和MLP层:
Mamba不使用Transformer的核心模块 - 注意力机制和MLP层。
取而代之的是一个融合了选择性状态空间模型和简单MLP的单一模块。 - 更简单和统一的结构:
通过移除Transformer中的复杂模块,Mamba的整体架构变得更加简单和统一。
整个模型只由重复堆叠的这种单一模块构成,没有像Transformer那样的复杂组件。 - 保留关键功能:
尽管去掉了注意力和MLP,但Mamba仍然能够通过选择性状态空间模型捕捉复杂的序列依赖关系。
同时还继承了状态空间模型的高效计算特性。
Mamba的设计思路是:在保留核心功能的前提下,最大限度地简化和统一模型结构,去除Transformer中一些复杂的组件。这使得整个模型更加简洁明了,同时也有利于提高效率和泛化性。这种简单而统一的架构设计是Mamba的一大创新之处。
mamba和其他模型的总结

具体可见 大佬的讲解
实验评估
Mamba 在一系列流行的下游零分评估任务上的表现。将这些模型与最著名的开源模型进行比较,最重要的是 Pythia 和 RWKV,它们使用与mamba模型相同的token、数据集和训练长度(300B token)进行训练。 (Mamba 和 Pythia 的训练上下文长度为 2048,而 RWKV 的训练上下文长度为 1024)。
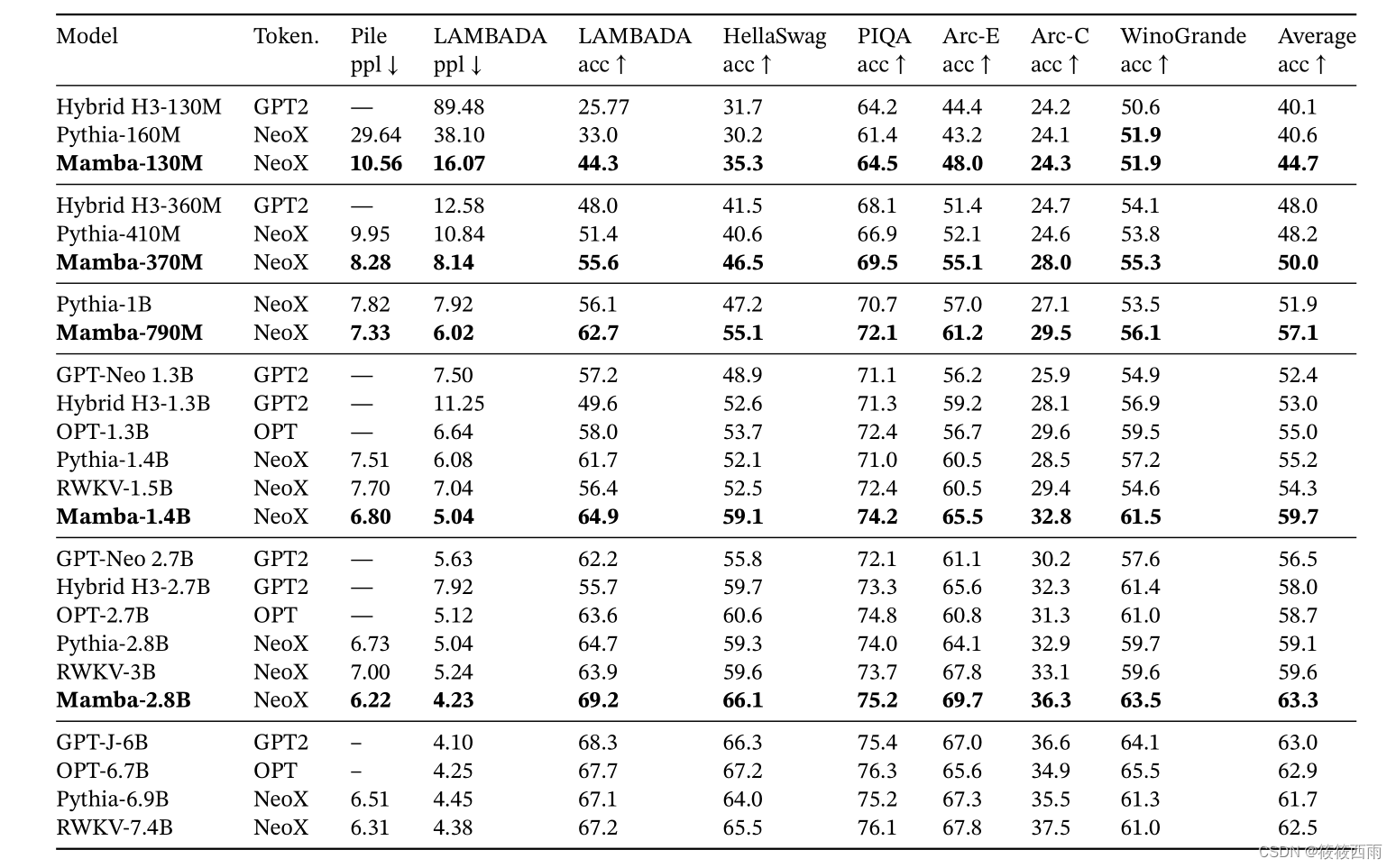
mamba的效果均优于比较的模型。
总结
Mamba 模型通过将选择性结构化状态空间模型 (SSM) 集成到简化的端到端神经网络架构中,显著提升了性能,特别是在缺乏传统注意力机制的情况下。Mamba-3B 模型的表现优于同尺寸的 Transformer,在性能上甚至可与两倍尺寸的 Transformer 相媲美。1.4B Mamba 语言模型的推理吞吐量是同类大小 Transformer 的 5 倍,其质量相当于两倍大小的 Transformer。在语言建模任务的预训练阶段和各种下游评估中,Mamba 显示出卓越的性能,超越了同类 Transformer 模型。
Mamba 的一个显著特点是其随着上下文长度的增加而逐步提高性能,能够有效管理多达一百万个元素的序列。这一特点突显了 Mamba 作为通用序列处理应用基础模型的多功能性和潜力,特别是在需要处理长上下文序列的新兴领域,如基因组学、音频和视频。其核心设计是一种专为结构化状态空间模型定制的新颖选择机制,使得模型能够执行上下文相关的推理,同时保持序列长度的线性可扩展性。
在序列长度的线性缩放方面,Mamba 通过~O(N) 的线性缩放颠覆了传统 Transformer ~O(N²) 二次缩放的规则,这一改进使 Mamba 能够有效处理多达一百万个元素的序列,这是当前 GPU 技术的一个壮举。
Mamba 通过高效利用更大数据集和网络,实现了更智能的结果,挑战了仅凭更多数据和更大网络就能提升性能的传统观念。针对 GPU 效率的优化设计,使 Mamba 解决了常见的计算效率低下问题,为机器学习架构的效率设立了新标准。
友情链接:
这是AIGC开放社区,信息共享平台,欢迎对AIGC与人工智能感兴趣的小伙伴们加入。
https://www.yuque.com/jasonxue/eruse9/wxtzlgluig4mgsyz

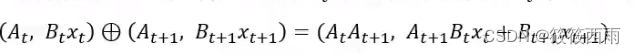








——体系:数据格式化——技术方法、主要工具)










)