第5章 整函数(复可积函数)(Entire Functions)
...but after the 15th of October I felt myself a free
man, with such longing for mathematical work, that
the last two months flew by quickly, and that only
today I found the letter of the 19th of October that I
had not answered. The result of my work, with which
I am not entirely satisfied, I want to share with you.
Firstly, in looking back at my lectures, a gap in
function theory needed to be filled. As you know, up
to now the following question had been unresolved.
Given an arbitrary sequence of complex numbers,
can one construct an entire (transcendental)
function that vanishes at these values, with prescribed
multiplicities, and nowhere else?...
(......但在10月15日之后,我感觉我自由了,我对数学工作如此渴望,过去的两个月过得很快,直到今天我才发现,10月19日的信我还没有回复。我的工作成果虽然我并不完全满意,但我想与大家分享。
首先,回顾我的讲座,函数论中的一个空白需要填补。如您所知,到目前为止,以下问题尚未解决。给定任意复数序列, 我们可以构造一个在这些值处(而不是其他地方)具有规定重数的复可积函数(超越函数)吗?... )
--------------------------------------------------------------------------------K. Weierstrass,1874
在本章中,我们将研究在整个复平面上全纯的函数,这些函数被称为复可积函数(entire functions)。我们的呈现将围绕以下三个问题进行:
(1) 这样的函数在何处消没?我们将看到,明显必要的条件也是有效的条件:若 是在 ℂ 中没有极限点的任意复数序列,则存在一个在这个序列点处恰好消没的复可积函数。这种期望的函数的结构是受到 sin(πz) 的 Euler 乘积公式的启发(典型情况是当
是 ℤ 时的情况),但还需要一个额外的补充条件:Weierstrass规范因子(或正则因子)(Weierstrass canonical factors)。
(2) 这些函数如何无限增长?在此,事情受到一个重要原则的控制:函数越大,它可以有的零就越多。这一原理已经在多项式的简单情况中得到体现。根据代数基本定理,d 次多项式 P 的零点数量正好是 d,这也是 P 的(多项式)增长阶中的指数,即
(当
时) 。
这个一般原理的精确版本包含在Jensen[jénsən]公式中,我们在第一部分中证明了这一点。这个公式是本章中大部分理论的核心,它展示了圆盘中函数的零点数量与圆上函数的(对数)平均值之间的深刻联系。事实上,Jensen公式不仅为我们构成了一个自然的起点,而且还引出了富有成效的价值分布理论,也称为Nevanlinna理论(不过,我们在这里不讨论它)。
(3) 这些函数在多大程度上由它们的零点决定?事实证明,如果复可积函数具有有限(指数)增长阶,则可以通过其零到乘以一个简单因子来指定它。 这个论断的精确版本是Hadamard因式分解定理。 它可以被视为第三章中阐述的一般原理的另一个实例,即在适当的条件下,全纯函数本质上由其零点决定。
1. Jensen公式(Jensen’s formula)
在本节,我们分别用 和
表示半径为 R 中心位于原点的开圆盘和圆。在本章的余下部分,我们也将排除恒为0的函数这种平凡情况。
定理 1.1 令 Ω 为包含圆盘 闭包的开集,并假设 f 在( f ≠ 0 ) Ω 中是全纯的且 f 在
上无处消没,若
表示 f 在圆盘内部的0(按重数计算)(注:即,每个零出现在序列中的次数与其阶一样)(译注:例如,某个0是5阶的,那么认为它出现了5次),则
(1) 。
分几步完成以上定理的证明。
第1步:首先我们注意到,假设 和
是两个满足假设条件和定理结论的函数,则它们的乘积
也满足定理的假设条件和公式(1)。这个观察结果是事实
(只要x和y是正数)的简单结果,并且
的 0 的集合是
和
的 0 的集合的并集。
第2步:函数
(起初定义于 ) 在每一个
附近是有界的。因此,每一个
都是一个可除奇点,因此,我们可以写成
,
其中,在 Ω 上是全纯的且在 的闭包中无处消没。按照第一步,只需证明类似 g 这样的无处消没的函数以及形如
的Jensen公式即可。
第3步:我们首先针对在 的闭包中无处消没的函数 g证明(1)。更确切说,我们必须建立如下的恒等式:
。
在一个稍大的圆盘中,我们可以写成 (其中,h在那个圆盘中是全纯的)。这是可能的,因为圆盘是简单连通的,故而我们可以定义
(见第3章中的定理6.2)。现在我们观察到
,
因此, 。 应用均值属性(第3章中的推论7.3)立即可得到预期的g的公式。
第4步:最后一步是证明形如 f (z) = z – w 的函数的公式(其中, )。即,我们必须证明
。
因为 和
,只需证明
( 只要 |a| < 1 )
即可。而这又等价于(在进行变量替换 θ ⟶ -θ 之后)
( 只要 |a| < 1 ) 。
要证明这一点,我们使用函数 F(z) = 1 – az ,它在单位圆盘的闭包中无处消没。结果,在半径大于 1 的圆盘中存在一个全纯函数 G ,使得 。则
因此,
。由于 F(0) = 1 ,我们有
, 应用均值属性(第3章中的推论7.3)到调和函数
就推断出了定理的证明。
从Jensen公式出发,我们可以推导出联系全纯函数与其在圆盘中的零的数量的恒等式。 若 f 在圆盘 的闭包中是全纯函数,我们用 𝖓(r)(或者,当有必要追踪问题中的函数的时候,使用
来表示 )来表示圆盘
中的 f 的0 的数目(按重数计算)。一个简单又有用的观察是,𝖓(r)是r的非递降函数。(译注:符号“𝖓”是德文尖角体活字小写,Unicode值是:1D593 ;LaTex名称:mathematical bold fraktur small n,语法 \mathfrak{n} 。)
我们断言,若 f (0) ≠ 0且 f 在圆 上不消没,则
(2) 。
这个公式直接来自Jensen等式和下面的引理
引理 1.2 若 是圆盘
内部的0点,则
。
证明:
首先,我们有
。
若我们定义特征函数
则 ,并使用
便证明了引理。
2. 有限阶函数(Functions of finite order)
令 f 为一个复可积函数。若存在一个整数 ρ 和两个常量 A,B > 0 ,使得
( 对于任意 z ∈ ℂ) ,
则我们称函数 f 具有一个ρ ≥ 0 的增阶(an order or growth),我们将函数 f 的增阶定义为
(infimum,下确界)
其中,下确界覆盖了使得 f 具有一个 ≤ ρ 的增阶的整个ρ > 0 范围。
例如,函数 的增阶是 2 。
定理 2.1 若 f 是一个具有≤ ρ的增阶的复可积函数,则:
( i ) 对于某个 C > 0 以及足够大的 r,有 。
( ii ) 若 表示 f 的 0 点,则对于任意 s > ρ 我们有
。
证明:
只需证明当 f (0) ≠ 0 时 𝖓( r ) 的估算值范围即可。事实上,考虑函数 (其中,𝓁 是 f 在原点处的的 0 的阶)。则
和
仅一常量之差,且 F也有一个≤ ρ 的增阶。
若 f (0) ≠ 0 ,我们可以使用公式(2) ,即
。
选择 R = 2r,这个公式意味着
。
在一方面,由于 𝖓(r) 是递增的,我们有
,
而在另一方面,f上的增长条件给出了
( 对于任意大的 r ) 。
因此,对于某个合适的 C > 0 和 任意足够大的 r , 。
下面的估算证明了定理的第二部分:
。
最后的级数收敛,因为 s > ρ 。
定理的第二部分是一个显著的事实,我们在本章的后面会用到这一事实。
我们给出这个定理的2个简单例子;其中的每一个都表明,条件 s > ρ 必不可少。
例子1:
考虑 f (z) = sin(πz)。回顾 Euler 恒等式,即
,
上式意味着 ,且 f 有一个 ≤ 1 的增阶。通过取 z = ix (其中,x∈ℝ),很显然可以看出,事实上,f 的增阶等于1 。然而,对于每一个 x∈ℤ ,在每一个 z = n 处,f 消没为 1 阶,并且当 s > 1时, 恰好有
。
例子2:
考虑函数 ,我们将其定义为
。
则 f 是复可积函数,并且容易看出
,
因此,f 的增阶是 1/2 。此外,当 时,函数 f (z) 消没,而当 s > 1/2时,恰好有
。
一个很自然的问题是,任给一个复数序列 , 在这个序列的这些处,是否恰当存在一个具有0值的复可积函数 f 。一个必要的条件是
不会累积,换句话说,我们一定有
,
否则,根据第2章定理4.8 ,函数 f 同样会消没。Weierstrass 通过显示构造具有这些规定0点的函数证明了这个条件也是有效的,首先猜测显然是乘式
,
当 0 序列有限的时候,这提供了一种特解。通常,Weierstrass证明的是如何在这个乘式中插入因子以确保其收敛性,而又不会引入新的0 。
在学习通用结构之前,我们复习一下无限积并研究一个基本例子。
3. 无限积(Infinite products)
3.1 通式(Generilities)
已知一个复数序列 ,若其部分积的极限
存在,则我们称积式
收敛。
下面的命题包含了一个确保积式存在的有用必要条件。
命题 3.1 若 , 则积式
收敛。此外,当且仅当其因子之一是0的时候,积式收敛于 0 。
这是第I 册第 8 章中的简单命题1.9 。在此,我们重复其证明。
证明:
若 收敛,则对于任意足够大的 n,我们一定有
。如有必要,不考虑有限多项后这个等式才成立,我们可以假设这个不等式对于任意 n 都成立。特别是,我们可以使用常见幂级数定义
(见第3章(6)),这个对数满足属性
(只要 |z| < 1 ) 。因此,我们可以将这个部分积写成如下形式:
,
其中, 且
。根据幂级数展开式我们看到,若 |z|<1/2 ,
。因此,
, 因此,
随着
而收敛于一个复数(比如,B )。因为指数函数是连续的,我们推断出随着
而
收敛于
这就证明了命题的第一个诊断。此外,观察到,若对于任意 n ,
,则这个积收敛于一个非零极限,因为它用
表达 。
更一般地,我们可以考虑全纯函数的乘积。
命题 3.2 假设 是开集 Ω 上的一个全纯函数序列。若存在常量
使得
且
( 对于任意 z∈Ω ),
则:
( i ) 积式 在Ω 上一致收敛于全纯函数 F(z)。
( ii ) 若 对于任意 n 不消没,则
。
证明:
为了证明第一种表述,注意到,对于每个 z ,若我们写成 , 则我们可以按前面命题的论证方法进行论证。然后,我们观察到,因为
是常量系,因此,这个估算结果事实是按 z 一致的。这就推导出了这个积式一致收敛于全纯函数,我们用 F(z) 表示这个函数。为了证明命题的第二部分,假设 K 是 Ω 的一个紧子集,并令
。
我们刚刚已经证明,在 Ω 中, 是一致的,因此,根据第2章中的定理 5.3 ,序列
在 K 中一致地收敛于
。因为
在 K 上从小一致有界,因此,是K 是 Ω 的一个任意紧子集,故而我们推断出在 K 上
是一致的,且又因为 K 是 Ω 的一个任意紧子集,因此,这个极限对于Ω 中的每一个点都成立。此如,正如我们第3章第4节中见到的那样,有
,
从而,命题的第二部分得证。
3.2 例子:正弦函数的积式(Example: the product formula for the sine function)
在进行Weierstrass乘积一般理论学习之前,我们考虑正弦函数乘积公式的主要例子:
(3) 。
接下来的这个恒等式可以从余切函数 ( ) 的求和公式推导出:
(4) 。
对于所有复数z ,第一个公式成立,而第二个公式当 n 不是整数时成立。需要正确地理解求和公式 ,因为对应正数和负数的单独一半的部分并不收敛。仅当按对
称解释时 ( 如 , 消没项才会导致如上(4)所示的收敛级数。
我们通过证明 和这个级数具有相同的结构属性,从而证明(4)。事实上,观察到,若
,则 F 具有下列三种属性:
(i) 只要 z 不是整数,则有 F(z + 1) = F (z) 。
(ii) , 其中
在 0 附近是解析的。
(iii) F(z)在整数处具有简单极点,且没有其它奇点。
则我们注意到函数
也满足以上三个属性。事实上,属性(i)只不过是这个观察结果——从 z 到 z + 1 这个通道(passage)仅仅是无限和中的项的平移。确切地说,
。
令 N 趋近于无穷大便证明了论断 (i)。根据求和表达式
, 属性(ii)和(iii)则不言自明。
因此,由
所定义的函数在Δ(z + 1) = Δ(z) 的意义上是周期性的,且根据(ii),Δ在原点的奇点是可除的,因此,按照周期性,函数在所有整数点处的奇点也是可除的;这意味着Δ是复可积函数。
为了证明我们的公式,只需证明函数Δ在复平面上有界即可。根据以上周期性,在带域 |Re(z)| ≤ 1/2 中这样做即可。这是因为,每一个 都具有形式
,其中,z在带域中,k是整数 。由于 Δ是全纯的,因此其在矩形域 |Im(z)| ≤ 1 中是有界的,则我们仅需针对 |Im(z)| > 1 控制这个函数的行为即可。若 |Im(z)| > 1 和 z = x + iy ,则
,
且按绝对值,这个量是有界的。此外
;
因此,若 y > 1 , 我们有
。
现在,上述不等式右侧的和优化为
因为函数
是按 x 递降的;此外,按照变量替换 x ⟼ yx 表明,积分独立于y,因此,积分式有界。按照类似的论证,Δ在带域中是有界的,其中,Im(z) < -1 ,因此,Δ 贯穿整个带域 |Re(z)| ≤ 1/2 有界。因此,Δ在整个ℂ中有界,根据 Liouville 定理,Δ(z) 是常量 。Δ是奇函数的观察结果表明,这个常量一定是0 ,从而推断出公式(4)的证明。
为了证明(3),我们现在令
和
。
命题 3.2 和事实 确保了积式 P(z) 收敛,则除了整数,我们有
。
由于 ,则由余切公式给出
,
以及对于某个常量 c 有 P(z) = c G(z)。用 z除以这个恒等式,并取 z⟶ 0 时的极限,我们求得 c = 1。
评注:
(4)和(3)的其它证明也可以通过解释类似 (由第3章练习12和第4章练习7推导出)的恒等式而给出。此外,使用 Fourier级数的其它证明可以在第I册的第 3章和第5章的练习中发现。
4. Weierstrass无限积(Weierstrass infinite products)
现在我们转向具有规定 0 的 Weierstrass 复可积函数结构。
定理 4.1 已知任意复数序列 , 且随着
而
,则存在一个在
处消没而在其它点无处消没的复可积函数 f 。任意其它这样的复可积函数都形如
, 其中,g(z) 也是复可积函数。
回顾一下,若一个全纯函数在 z = a 处消没,则 a 处0点的重数是使得
的整数 m ,其中,g 是全纯函数且在 a 的领域内无处消没。或者,m 是 f 在 a 点的幂级数展开式中 (z - a) 的第一个非零幂。因此,如前一样,我们允许序列 中有重复项,这个定理事实上确保了具有规定和期望重数的复可积函数的存在。
为了开始证明,首先注意到,若 和
是2个在任意
处消没而在其它点处无处消没的复可积函数,则
是复可积函数且无处消没,因此,存在一个满足
的复可积函数 g (如第3章第6节中所示)。因此,
,则这个定理的最后一部分得到验证。
因此,我们剩下的任务是构造一个在序列 的所有点消没而在其它点处无处消没的函数。一个不成熟的(naive)猜测是积式
(通过
的乘积公式证明)。问题在于,这个积式仅对合适的序列
收敛,因此,我们通过插入指数因子来纠正这个问题。这些因子将使得乘式在无需加入新的零点的情况下收敛。
对于每一个 k ≥ 0 , 我们定义规范因子(canonical factors)为
和
( 对于 k ≥ 1) 。
称这个 k 为规范因子的阶(degree)。
引理 4.2 若 |z|≤ 1/2 ,则对于某个 c > 0 ,有 。
证明:
若 |z|≤ 1/2 ,则对于根据幂级数定义的对数,我们有 , 因此,
,
其中, 。观察到,由于 |z|≤ 1/2 ,我们有
。
特别是,我们有 |w | ≤ 1 ,则这意味着
。
评注:
一个重要的技巧点是,在引理表达式中,可以选择独立于k 的常量 c 。事实上,对证明的考察表明,我们可以取 ,则 c = 2e 。
假设已知一个原点的 m 阶0,并且 均为非零值。则我们定义 Weierstrass 积式为
。
我们断言,这个函数具有所要求的属性;即,f 是一个复可积函数,它在原点具有一个m阶0以及在序列 的每个点处为零,而在其它点无处消没。
因定 R > 0 ,假设 z 属于圆盘 | z | < R 。我们将证明, f在圆盘中具有所有预期属性。因为R是任意的,这将能证明定理。
我们可以考虑定义 f 的公式中的两种因子,根据所依赖的选择是 还是
。仅存在有限多项第一种类型(因为
),我们看到,有限积在所有
处消没 (
) 。若
,我们有
,因此,前面的引理意味着
。
注意,根据上述评注,c 不取决于 n。因此,当 | z | < R 时,积式
定义了一个全纯函数,根据第3节中的命题,这个全纯函数在圆盘中不消没。这就证明了函数 f 具有预期的属性,因此,Weierstrass 定理的证明完成。
5. Hadamard[adamá:r]因式分解定理(Hadamard’s factorization theorem)
本节的定理结合了函数增长与其拥有的零个数相关的结果以及上述乘积定理。
Weierstrass 定理指出,在 处消没的函数采用
的形式。Hadamard 通过证明在有限阶函数的情况下,可以将规范因子的次数视为常数,并且 g 是一个多项式来完善该结果。
回顾一下,对于一个复可积函数,若
( 对于任意 z ∈ ℂ) ,
则其有一个 ≤ ρ 的增阶,并且 f 的 增阶是所有像ρ 这样的增阶的下界确(infimum)。
我们在前面证明的一个基本结论是,若 f 具有一个 ≤ ρ 的增阶,则
( 对于任意大的 r ),
且若 是 f 的非零的零点且 s > ρ ,则
。
定理 5.1 假设 f 是复可积函数且具有增长阶 。令 k 为使
的整数。若
是 f 的非零的零点,则
,
其中,P是一个阶 ≤ k 的多项式,m是 f 在 z = 0 处的零的阶。
主引理
在此我们汇聚几个在证明Hadamard定理的过程中需要用到的引理。
引理 5.2 规范积满足
( 若 | z |≤ 1/2 )
和
( 若 | z |≥ 1/2 ) 。
证明:
若 | z | ≤ 1/2 ,我们可以使用幂级数来定义(1 - z) 的对数,因此,
。
因为 和
,引理的第一部分可证。
对于引理的第二部分,只需注意到,若 | z |≥ 1/2 ,则
,
并且,存在 使得
。
当| z |≥ 1/2 时,则引理中的不等式可从这些观察推导出。
证明Hadamard定理的关键在于,找到当 z 远离零 时规范因子乘积的下界。 因此,我们首先要在以这些点为中心的小圆盘的补集中估算下面的乘积。
引理5.3 对于满足 的任意 s,我们有
( 除去当 z 属于半径为
圆心位于
的圆盘的并集这种可能(对于 n = 1, 2, 3, ......))。
证明:
这个引理的证明有一点微秒。首先,我们写成
。
对于第二个积式,上述估算的论断对于 z上的非限制也成立。事实上,根据前面的引理,
。
但是, 和 s < k + 1 , 因此,我们一定有
。
因此, 收敛这个事实意味着对于某个 c > 0,有
。
为了估算第一个积式,我们使用引理5.2的第二部分,并写成
(5) 。
现在我们注意到
,
再一次地,我们有 ,据此,证明了
。
它是对 (5) 右侧第一个乘积的估计,要求在引理的表述中对 z 施加限制。事实上,只要 z 不属于圆心位于 半径为
的圆盘,我们就一定有
。因此,
。
最后,对于第一部分积式的估算,可由以下事实推出:对于任意 ,
,
并且按照定理 2.1, 第二个不等式也可推导,因为 。因为我们限定
, 我们可以取一个足够接近
的初始 s ,因此,这个引理的论断得证(用
替代 s)。
推论5.4 存在一个半径序列 , 且
,使得对于
,有
。
证明:
因为 ,则存在一个整数 N 使得
。
因此,已知任意两个连续的任意大整数 L和 L + 1 ,我们可以求得一个正整数 r (L ≤ r ≤ L + 1 ),使得以 r 为半径以原点为圆点的圆与引理5.3中被除去的圆盘不相交。否则,区间的并集
(长度为 ) 会覆盖整个区间 [L , L + 1]。(见图1。) 这意味着,
, 这就得出了矛盾。我们可以在 |z|= r 的情况应用前面的引理推导出推论的证明。
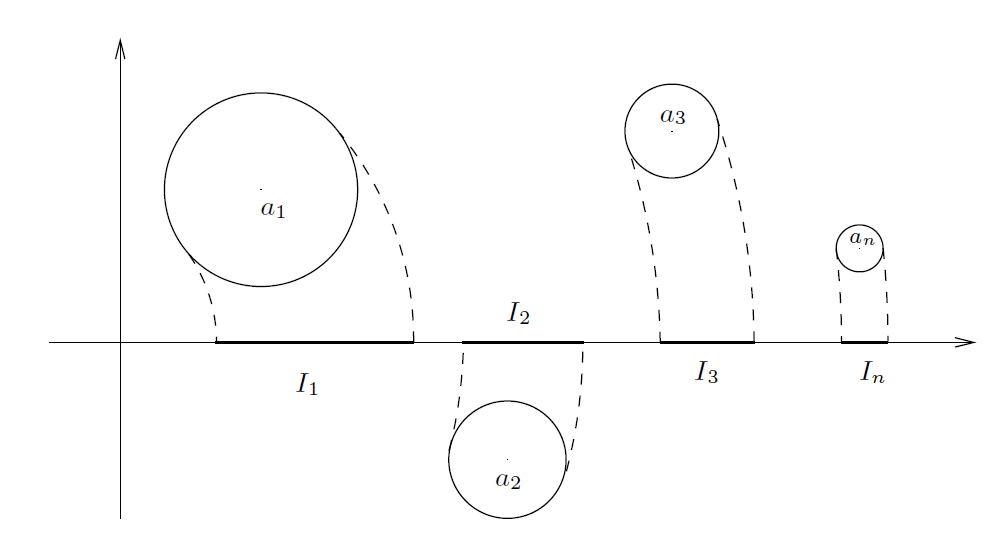
-----------------------------------------------------图1: 区间 --------------------------------------------------
Hadamard 定理的证明
令 。
为了证明 E 是复可积函数,我们重复应用定理4.1的证明中的论证方法;按引理4.2 ,我们考虑
( 对于任意大的 n ) ,
且级数 收敛。(回顾
。) 此外,E 具有 f 的0,因此,f / E 是全纯函数且无处消没。故而,对于某个复可积函数 g 有
。
根据 f 有 增阶的事实,以及由于下列按推论5.4 而获得的对 E 的估算,则对于
我们有
。
这证明了对于 ,
。若我们可以建立下面最后的引理,则就可以完成对Hadamard定理的证明。
引理 5.5 假设 g 是复可积函数且 u = Re(g) 满足对于一系列趋近于无穷大的正实数 r ,只要 |z| = r ,就有
,
则 g 是一个阶 ≤ s 的多项式。
证明:
我们可以按中心位于原点的幂级数展开函数 g 为
。
在第3章的最后一节(作为Cauchy积分公式的简单应用)我们已经证明了
(6) 。
通过取复数共轭我们求得
(7) ( 只要 n ≥ 0 ) ,
又因为 , 我们将 (6)和 (7) 相加得到
( 只要 n ≥ 0 )。
对于 n = 0 ,我们可以简单地对(6)式两侧取实部而求得
。
现在我们回顾这个简单事实——只要 n ≠ 0 , 在任意以原点为圆心的圆域上的积分消没。因此,
(只要 n ≥ 0) ,
因此,
。
令 r 沿着引理的假设中给出的序列趋近于无穷大便证明了,对于 n > s ,有 。这就完成了对引理的证明,从而完成了对 Hadamard 定理的证明。
内容来源:
<< Complex Analysis >> ,作者:E.M. Stein & R. Shakarchi
术语参考资料:
<<英汉数学词汇>>,张鸿林,葛显良 编订,清华大学比版社,2018年
<<新英汉数学词汇>> ,科学出版社名词室,科学出版社, 2002年
<<物理学名词>>,第三版,科学出版社会,2019年
<<英汉综合物理学词汇>> 科学出版社,1999年


![[机器学习算法] 主成分分析](http://pic.xiahunao.cn/[机器学习算法] 主成分分析)












)



)