线性方程组

解方程组的变换就是矩阵初等行变换

三秩相等

方程组系数矩阵的行秩=列秩，线性相关的问题应求列秩，但求行秩方便

齐次线性方程组

对应向量组的线性相关，所以回顾下线性相关的知识：


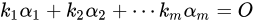
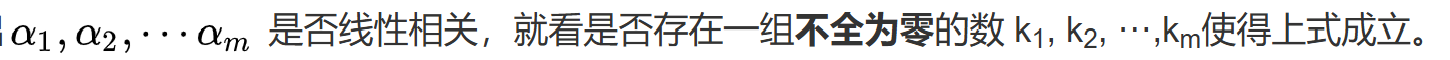
其中k是x，所以用向量组判断线性相关的办法判断方程组的解的情况，所以线性相关=有非零解，即r(A_mn)<n时有非零解

而r(A)≤min{m,n }，当m<n（方程个数小于未知数个数）时，r(A)≤m<n，方程组有非零解
当m=n时，若r(A)<m=n则有非零解

非齐次线性方程组

对应向量组的线性表示

r₁、r₂是Ax=b的解，则r₁-r₂是Ax=0的解

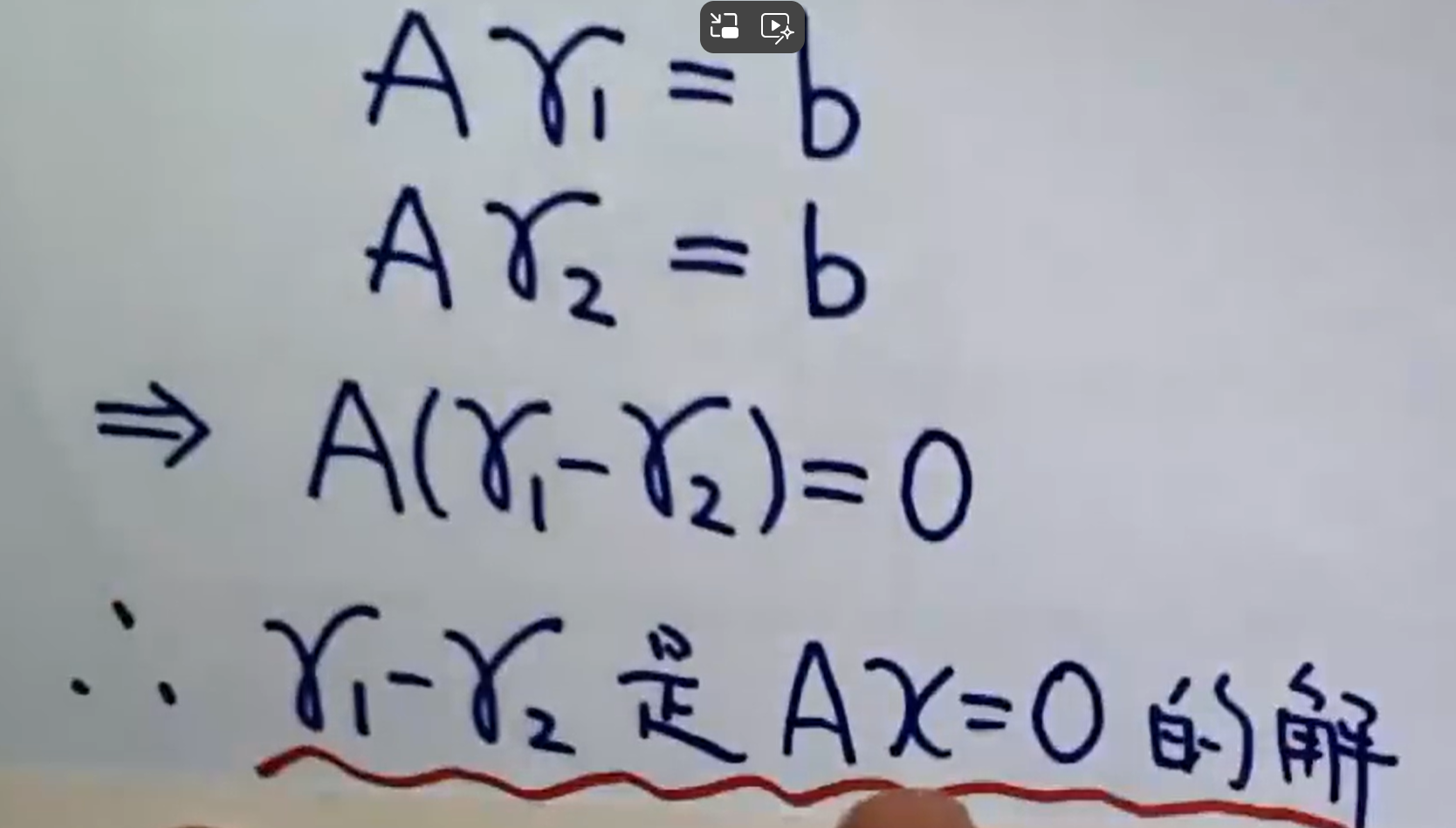
线性无关解的个数s=n-r(A)是齐次的，而非齐次s≤n-r(A)+1，所以有了非齐次的线性无关解的个数无法判断齐次线性无关解的个数，也无法直接判断r(A)