机器学习作业7—

机器学习作业7——PCA

一、原理

1.数据中心化

2.白数据与目标

3.协方差与协方差矩阵

4.特征值与特征向量

5.最终结果构造

二、代码

代码解释：

三、结果

结果解释：

pca优缺点分析：

参考视频：

一、原理

目的：

pca是为了将原始的数据集的特征维度减少。

如上图，横纵坐标代表两个特征，可以看到这两个特征正相关程度很大，都快可以用一条直线连起来了。

假如能把它变成像下图这样的，能很大程度的保留样本点的信息，又能够减少特征维度，那就实现了pca的降维（将两个特征用一个主成分表示）。

一些概念：

1.数据中心化

假设原来的数据是二维的，并且将样本点放在坐标系中是这样

中心化后，结果如下图。

实现：

对每个特征，先求出他的均值：

$\bar{x} = \frac{1}{N} \sum_{i=1}^N x_i$

再将每个样本的该特征，都减去这个均值

$\tilde{x}_i = x_i - \bar{x}$

对每个特征都执行了这样的操作就结束了。

2.白数据与目标

先假设假设数据中心化后如左图，为了引出目标，假设右图就是他的白数据。

变成

设白数据样本集为

样本的特征x和特征y是独立的，并且服从标准正态分布。

其中D是样本集，列数是样本数量，行数为特征数量。

拉伸：

现将一个矩阵乘上数据集，得到：

结果如下图

就可以实现将这个样本集在X轴上“拉长”

旋转：

假设SD左乘一个矩阵，就变为下图：

现在我们手上的数据便是这个“RSD”，其中这个R是最重要的，PCA需要求出这个矩阵R，也就是旋转坐标轴的角度。

一些补充：

3.协方差与协方差矩阵

协方差定义：

$\text{Cov}(X, Y) = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y})$

其中：n 是样本数量，Xi 和 Yi 分别表示第 i 个样本的 X 和 Y 值， $\bar{X},\bar{Y}$ 分别是 X 和 Y 的均值。

在PCA中，X和Y即为特征。

协方差的意义是：表示X与Y的相关程度，若正相关，协方差大于0，负相关则小于0，若几乎为0，则不相关。

显然的，当Y=X时，协方差分子即为方差。

由于已经去中心化了，所以均值都为0。

协方差矩阵：

将协方差带入：

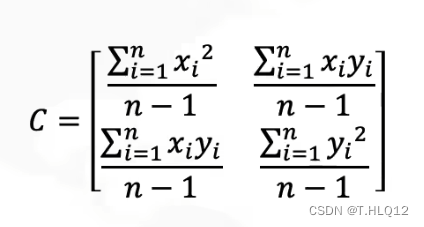
其中D是上面的白数据。

将D替换为RSD，则已经中心化后的数据的协方差矩阵为：

第4行中，因为，其中白数据的X与Y是不相关的，所以协方差为0，而对角线上为方差，并且X与Y是标准正态分布，所以为1。

第5行中，RT = R-1在上面有补充，第6行中，L定义为S*ST。

算完这个玩意之后，自然有用处，和接下来的式子形式上相同。

4.特征值与特征向量

假如以下式子成立

$\mathbf{A} \mathbf{v} = \lambda \mathbf{v}$ ，其中A为矩阵，v为列数为1，行数与A相等的矩阵， $\lambda$ 为标量。

那么v就为矩阵A的特征向量， $\lambda$ 就为特征值。

现在先给出以下两个式子（因为现在假设原数据集特征维度为2）

由线性代数基础知识，可由上两式得到：

可以看作：

两边同右乘R-1，又因为R-1=RT，所以得到：

便可以将R中第一列看作特征向量1，第二列看作特征向量2。

这样，求解这个R，就是求出了特征向量了。

而L则是特征值。

5.最终结果构造

求出了这个R后，根据特征值大小对特征向量进行排序，选择前几个特征向量对应的主成分，这些主成分能够解释数据中最多的方差。

然后构造特征向量矩阵：将选择的主要特征向量排列成一个矩阵。假设选择了 k 个主成分，那么这个矩阵的大小将是 d*k，d是原始数据的维度

将中心化后的数据矩阵 X 乘以特征向量矩阵 W，得到的数据矩阵 Z = XW 的大小为 n * k，即为最终结果。

二、代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaleriris = datasets.load_iris()
X = iris.data
y = iris.targetscaler = StandardScaler()
X_scaled = scaler.fit_transform(X)pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)#创建一个图形并设置子图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))#降维前的数据前两个特征
ax1.set_title("origin")
for i, target_name in zip([0, 1, 2], iris.target_names):ax1.scatter(X[y == i, 0], X[y == i, 1], label=target_name)
ax1.set_xlabel('X1')
ax1.set_ylabel('X2')
ax1.legend()#降维后的数据
ax2.set_title("after")
for i, target_name in zip([0, 1, 2], iris.target_names):ax2.scatter(X_pca[y == i, 0], X_pca[y == i, 1], label=target_name)
ax2.set_xlabel('X1')
ax2.set_ylabel('X2')
ax2.legend()plt.show()

代码解释：

由于这次老师说可以用库函数，所以比较简单。

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

这里是主要部分，第一行就是创建个pca对象，指定主成分数量为2（也就是接下来往这个对象中传入数据，返回出来的是二维特征的数据），然后第二行就是将数据集扔进去，也就是X_scaled,

返回的X_pca即是处理完的数据集。

三、结果

结果解释：

使用鸢尾花数据集来作为本次实验的数据集。

左图是原数据使用前两个特征展现出的图，右图是pca的结果。

可以看到左图的黄绿点比较混杂，而右图的黄绿点左右分的比较开，两张图的蓝点都比黄绿点分的开。而把黄绿点分的比左图开的右图，就是pca的功劳与结果。

pca优缺点分析：

优点：

降低数据维度：PCA通过投影数据到较低维度的主成分空间，实现了数据的降维。这有助于减少数据存储和计算成本，并简化后续分析过程。
消除特征间相关性：PCA通过转换数据，使得新的特征向量（主成分）之间彼此正交，从而消除原始特征之间的相关性。这有助于减少多重共线性问题，并提高后续模型的准确性和稳定性。
保留最大方差信息：PCA将数据投影到方差最大的主成分上，这意味着它保留了数据中最重要的信息。这使得我们能够更好地理解数据集的结构和变异性，以及更好地解释数据。
可视化数据：降维后的数据可以更容易地可视化，因为它们通常只涉及两个或三个主成分。这有助于发现数据中的模式、聚类和异常值。

缺点：

信息损失：降维过程中，为了将数据映射到较低维度，必然会丢失一部分信息。降维后的数据无法完全还原原始数据，因此可能会损失一些细节和特征。
主成分的可解释性：虽然PCA可以帮助我们找到方差最大的主成分，但这些主成分通常很难直接解释。它们是原始特征的线性组合，因此不容易与现实世界中的具体含义对应。
对离群值敏感：PCA对离群值比较敏感，因为它是基于数据的协方差矩阵或相关矩阵计算的。离群值可能会对协方差或相关性的计算产生较大的影响，从而导致降维结果不准确。
计算复杂性：PCA的计算复杂度较高，特别是在处理大规模数据集时。计算协方差矩阵或相关矩阵需要较大的计算和存储开销。