1 输电线路故障仿真模型
基于双端行波测距理论,在MATLAB软件中搭建的三相50Hz的输电线路故障仿真模型如图1所示,该模型包含了三相电源、输电线路、故障发生器和示波器模块等。主要仿真参数设置如下:仿真时间为 0~0.1s,采用固定步长 10-7和ode3 算法,故障转换时间为[0.035,0.1],频率Frequency=50Hz,在各示波器中将采样数据格式设置为矩阵形式并将结果保存至MABLAB的workspace中。
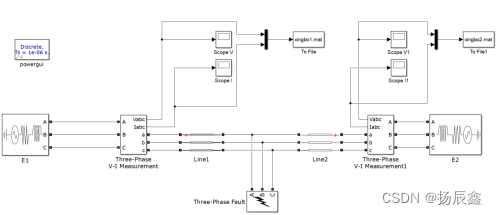
图 1 输电线路故障仿真模型
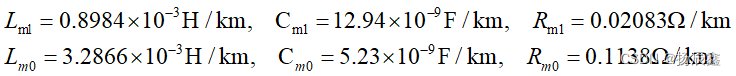
E1,E2的线电压有效值均为500kV,A相相角分别为0º和30º,l1线路长度为100km,l2线路长为200km。
根据仿真后所得的三相电压和三相电流数据可以提取故障发生时正反向电压行波和正反向电流行波,具体的提取方法步骤如下:利用故障后的一段时间的三相电压和电流值减去故障前的一段时间的相电压和电流值就可以得到故障三相电压和三相电流的暂态值,分别设暂态量为u和i。
因为三相的暂态量并不是孤立的,它们互相之间存在合,所以需要把相的分量转成独立的模分量,从而利用模量行波来实现相应功能,这里可以用Clarke 变换得到模分量,计算过程如下:
Clarke变换矩阵为:

电压模量计算:

2 仿真结果分析
首先用故障后一段时间的电压值减去故障前一段时间的电压值得到电压的暂态量,再利用式和进行Clarke变换得到相应的模分量,计算得到正反向行波的模分量,通过编程仿真得到E1和E2端的a模量的正反向的电压行波,如图 2 和图 3 所示。

图 2 E1 端电压模量的正向和反向行波
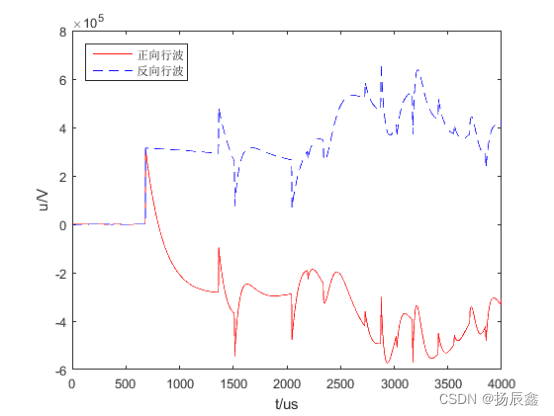
图 3 E2 端电压模量的正向和反向行波
接下来就是对E1和E2端电压的反向行波进行小波变换得到小波变换系数,根据模极大值理论,找出各波头的时刻值。之所以选择反向行波进行小波变换,是因为反向行波检测可以有效地避免对端母线折射过来的波头的影响。用db5小波进行3层分解,并取第2层,得到E1和E2端电压行波变换后的小波系数如图 4和图 5所示。

图 4 E1 端反向行波的小波变换
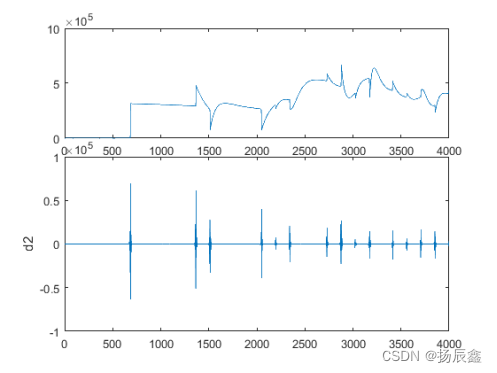
图 5 E2 端反向行波的小波变换
由图4 可以清楚地看出,E1新信号的突变点出现的时刻t1=343μs,由图5可以清楚地看出E2端信号的突变点出现的时刻为t2=685μs。
行波的波速的计算如下:
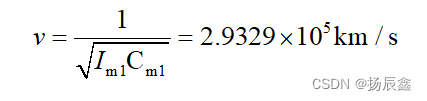
绝对误差表示为:
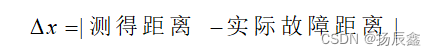
双端测距的计算公式如下:

式中,x1是故障点到E1端的距离,t1,t2是故障行波到达线路两端母线的时间值,X线路总长为300km,依据和可得x1=99.8473km,∆x=0.1527km,绝对误差为0.1527%。
)

 - 双击跳转到另外一个ALV)





)
)



)





