我绝对不会告诉你我是因为太蒻了，不会 FFT 才搞这个的。

我用一下别人的图没什么问题吧

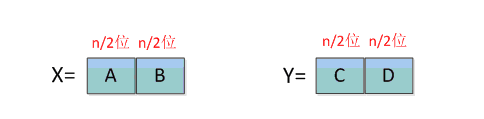
看得懂吧？比如 $X=123456,Y=987654$，则 $n=3,A=123,B=456,C=987,D=654$。

前置知识：整数末尾添 $0$ 方法（不可能不会吧），就是乘 $10$，当然添 $n$ 个零就是乘 $10^n$，$\frac{n}{2}$ 个就是乘 $10^{\frac{n}{2}}$。

失败……

接下来！
$$\because X=A\times 10^{\frac{n}{2}}+B,Y=C\times 10^{\frac{n}{2}}+D$$
$$\therefore \begin{array}{rl}X\times Y=& (A\times 10^{\frac{n}{2}}+B)\times (C\times 10^{\frac{n}{2}}+D)\\ =& AC\times 10^n+AD\times 10^{\frac{n}{2}}+BC\times 10^{\frac{n}{2}}+BD\\ =& AC\times 10^n+(AD+BC)\times 10^{\frac{n}{2}}+BD\end{array}$$
需要进行 $4$ 次乘法（$10^k$ 不算，因为是直接添 $0$）。
所以时间复杂度 $T(n)=4T(\frac{n}{2})$。
也就是一棵满四叉树，节点数很多，不过只需要关心最后一层。
最后一层有 $4^k$ 个节点，$k$ 为高度（根节点其实为 $0$，但是其实都是细节，无伤大雅），$k=lo{g}_{2}n$。
所以，时间复杂度为 $O(4^{lo{g}_{2}n})$，也就是：
$$\begin{array}{rl}& \\ & O(4^{{\log }_{2}n})\\ =& O((2^2{)}^{{\log }_{2}n})\\ =& O(2^{2{\log }_{2}n})\\ =& O((2^{{\log }_{2}n}{)}^2)\\ =& O(n^2)\end{array}$$
谔谔，为什么还是 $O(n^2)$，这不和原本一样吗ToT。

成功

我们观察式子：
$$AC\times 10^n+(AD+BC)\times 10^{\frac{n}{2}}+BD$$
发现它有三个部分，答案是这三个部分的和：

1. $AC\times 10^n$ 一次乘法
2. $(AD+BC)\times 10^{\frac{n}{2}}$ 两次乘法
3. $BD\times 10^0$ 一次乘法

发现就是第二个部分乘法次数最多。
考虑将其优化。
直接优化（化简）：很难，想不出来。
但是，如果式子中用了 $AC$ 或 $BD$，则不会增加乘法次数，因为有重复，可以记录下来。
简单起见，我们关注前半段：$AD+BC$，考虑将其变为 $??+AC+BD$。
$$\begin{array}{rl}& \\ & AD+BC-AC-BD\\ =& A(D-C)+B(C-D)\\ =& A(D-C)-B(D-C)\\ =& (A-B)(D-C)\end{array}$$
现在，只需要进行一次乘法。最终公式：
$$AC\times 10^n+((A-B)(D-C)+AC+BD)\times 10^{\frac{n}{2}}+BD$$
时间复杂度：
$$\begin{array}{rl}& \\ T(n)=& 3T(\frac{n}{2})\\ =& 3^{{\log }_{2}n}\\ =& (2^{{\log }_{2}3}{)}^{{\log }_{2}n}\\ =& (2^{{\log }_{2}n}{)}^{{\log }_{2}3}\\ =& n^{lo{g}_{2}3}\end{array}$$
那么 ${\log }_{2}3$ 大约是多少呢？${\log }_{2}3\approx 1.585$。
那么到底是多少呢？来不严谨地粗略估计一下：
假设计算机每秒可以执行 $10^8$ 条指令。
则最大可以计算的位数为：$n^{{\log }_{2}3}=10^8$，则位数最大约为 $111541$。
而对比朴素算法 $O(n^2)$，最大位数仅为 $10000$，相比之下多了一个多数量级！