CSS函数：fit-content与matrix的使用

网格函数

fit-content()属于网格函数，除此之外的网格函数还有：CSS函数：实现数据限阈的数字函数。顾名思义，这三个函数只能在网格布局中使用。fit-content()函数主要是用于给定布局可用大小，适应内容，其功能等同于：min(maximum size, max(minimum size, argument))。函数格式如下：

/* <length> values */
fit-content(200px)
fit-content(5cm)
fit-content(30vw)
fit-content(100ch)/* <percentage> value */
fit-content(40%)

fit-content()接收一个参数，可以是长度值或者是百分比值，当为长度值时支持各种格式的固定长度，如：px、cm、vw、ch等。当参数为百分比值，相对于给定轴中可用空间的百分比。在网格属性中，它与列轨道中网格容器的内联大小和行轨道中网格容器的块大小相关。否则，它与布局框的可用内联大小或块大小相关，具体取决于书写模式。

浏览器兼容性

使用示例

如下通过示例来理解fit-content()函数具体的使用方式和布局配置理解。

<!DOCTYPE html>
<html lang="en"><head><meta charset="UTF-8"><meta name="viewport" content="width=device-width,initial-scale=1.0"><meta http-equiv="X-UA-Compatible" content="ie=edge"><title>fit-content函数实现内容自适应示例</title><style>#container {display: grid;grid-template-columns: fit-content(300px) fit-content(300px) 1fr;grid-gap: 5px;box-sizing: border-box;height: 200px;width: 100%;background-color: #8cffa0;padding: 10px;}#container>div {background-color: #8ca0ff;padding: 5px;}</style>
</head><body><div id="container"><div>与内容等宽.</div><div>根据给定内容，当内容小于300px，则宽度与内容等宽，当内容大于300px，则宽度为300px.</div><div>弹性宽度</div></div></body></html>

展示样式：

从上方的示例可以看出，当给定的内容大于设置宽度，则容器宽度等于设置宽度，内容自动换行，当给定内容小于设置宽度则容器宽度等于内容宽度。

示例源码：fit-content函数实现内容自适应示例

转换函数

CSS函数matrix()应用于transform设置转换动画，matrix提供六个参数实现一个3*3的矩阵镜像坐标转换成2D坐标。其语法格式如下：

matrix(a, b, c, d, tx, ty)

如上，该函数需要接收六个参数来实现2D坐标的转换：

a b c d：用于描述线性变换
tx：用于描述x轴上的线性平移
ty：用于描述y轴上的线性平移

matrix()的特殊值可以通过设置特殊值设置效果：缩放、旋转、移动、倾斜功能。matrix转换的矩阵:

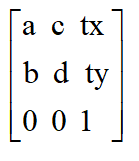
根据上述举证，我们对比常用的缩放、旋转、移动、倾斜功能的矩阵格式如下：

通过上述，我们可以梳理特殊效果的matrix()设置方式：

scale(x)：等同于matrix(x,0,0,x,0,0)，x轴和y轴同等缩放
scaleX(x)：等同于matrix(x,0,0,1,0,0)，x轴缩放
scaleY(y)：等同于matrix(1,0,0,y,0,0)，y轴缩放
translate(x,y)：等同于matrix(1,0,0,1,x,y)，位移转换，x代表x轴位移，y代表y轴位移
translateX(x)：等同于maxtrix(1,0,0,1,x,0)，位移动画，x轴位移
translateY(y)：等同于maxtrix(1,0,0,1,0,y)，位移动画，y轴位移
skew(x,y)：等同于maxtrix(1,tan(x),tan(y),1,0,0)，倾斜，x轴和y轴倾斜的角度
skewX(x)：等同于maxtrix(1,tan(x),0,1,0,0)，x轴倾斜
skewY(y)：等同于maxtrix(1,0,tan(y),1,0,0)，y轴倾斜
rotate(x)：等同于maxtrix(cos(x),-sin(x),sin(x),cos(x),0,0)，顺时针旋转x（如30deg）

下面通过一个示例来了解下如何使用。

<!DOCTYPE html>
<html lang="en"><head><meta charset="UTF-8"><meta name="viewport" content="width=device-width,initial-scale=1.0"><meta http-equiv="X-UA-Compatible" content="ie=edge"><title>CSS matrix函数使用</title><style>body {text-align: center;}h1 {color: green; // 设置颜色}.matrix {transform-origin: 0 0;transform: matrix(.4,0,0,2,0,0);font-size: 26px;font-weight: bold;width: 250px;padding: 20px;background: green;color: white;font-family: sans-serif;}</style>
</head><body><h1>CSS matrix函数使用</h1><br><br><div class="matrix">Matrix转换区块（x缩小为0.4,y放大为2倍）</div>
</body></html>

效果如下：