汉诺塔问题的大概

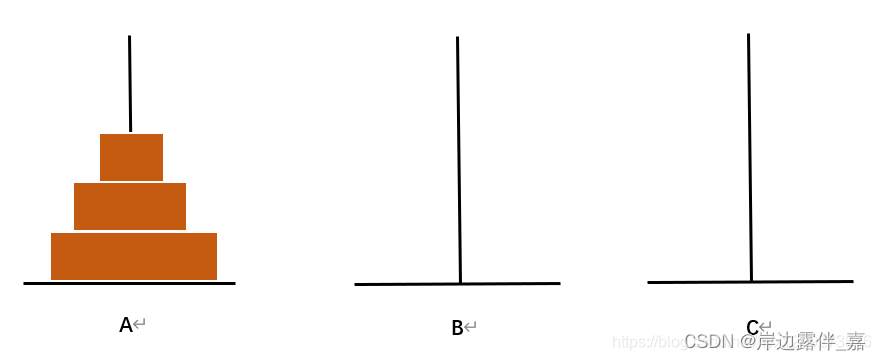
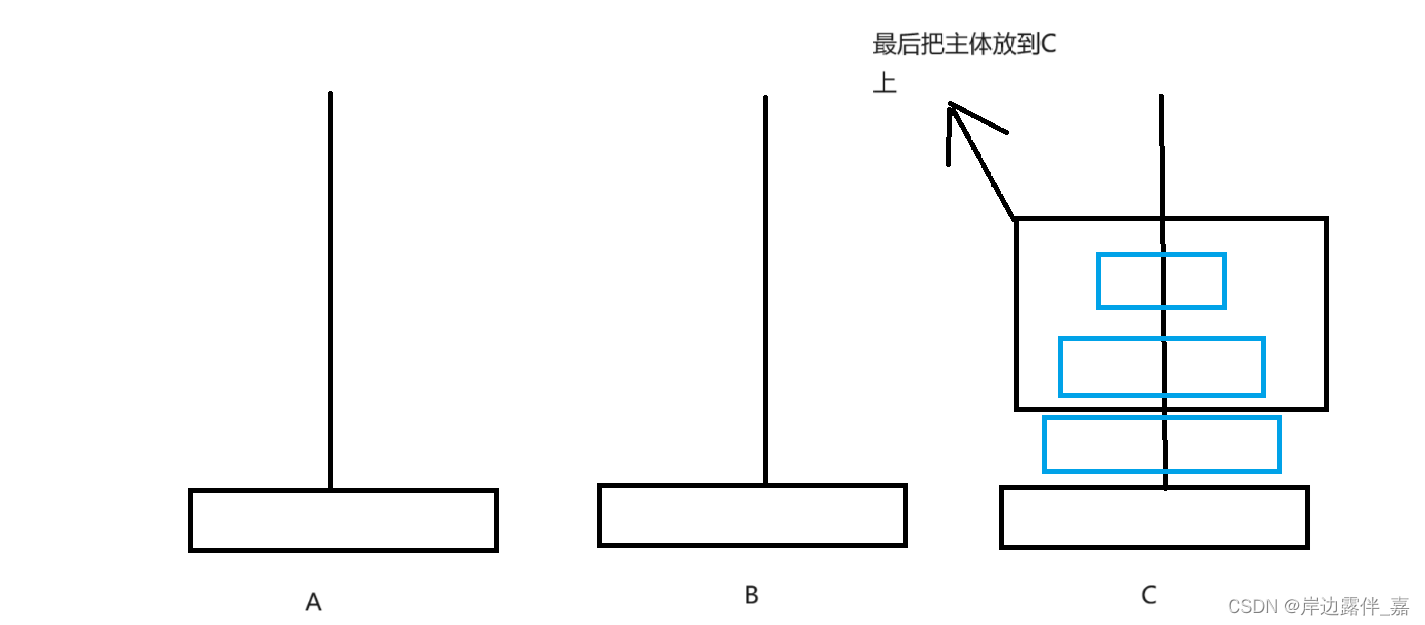
 汉诺塔问题如图三个柱子，利用B将A上面的盘子移到C上面，但是一次只能移动一个盘子并且大的盘子不可以在小的盘子上面。

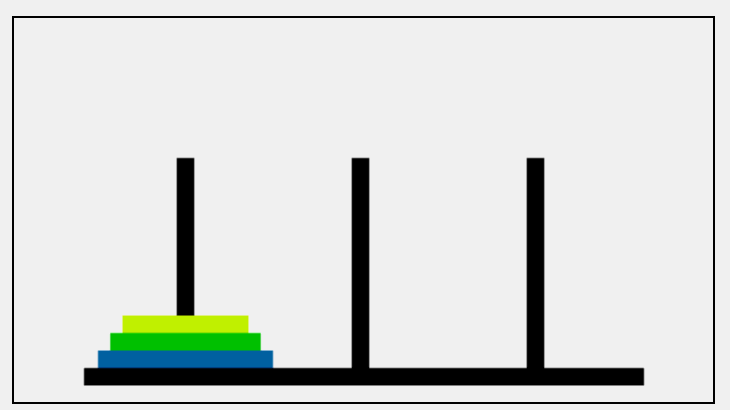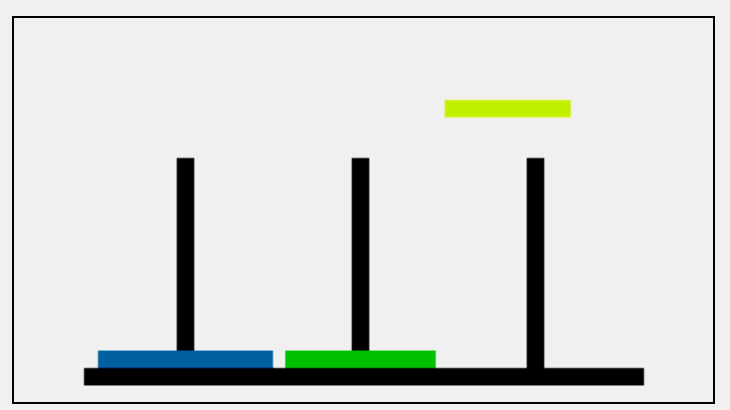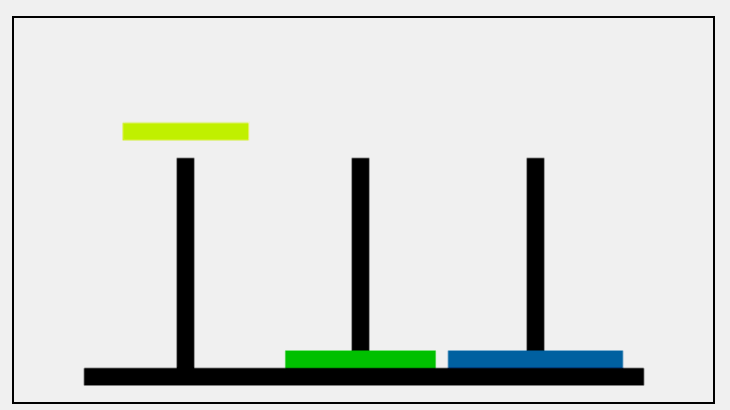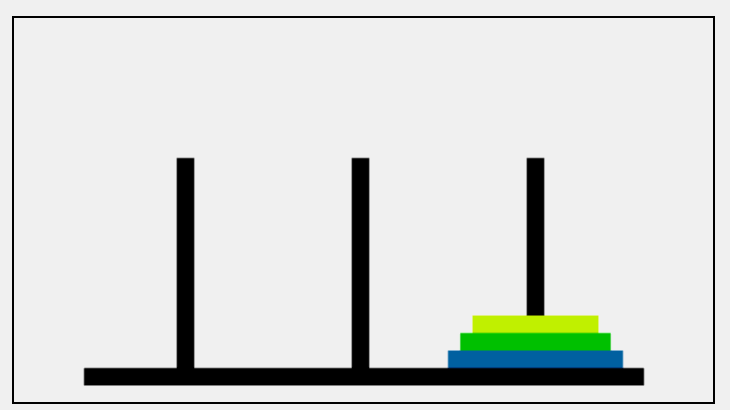
 当只有三个盘子的时候，就像图片一样移动，当盘子多了起来我们就很难分得清逻辑了。

这个时候我们就可以用递归思维来解决这个问题，递归的要点就是大事化小，小事化了。

递归实现思路

 第一步：

 

 

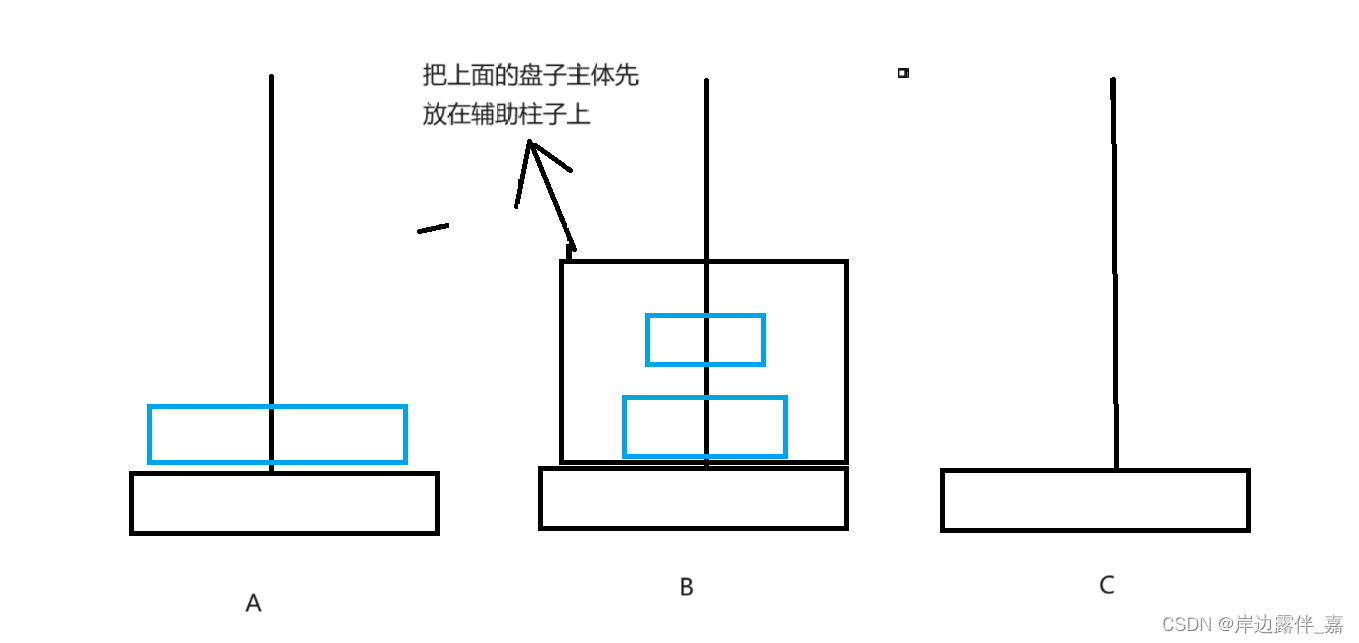
第二步：

 

第三步：

 

 大家可能会很疑惑，不是说一次只能移动一个吗，其实递归思想就是这样，我们要把他简化，把上述的主体就看做一个盘子，这就是我们写代码的基本思路了，接下来我们就写代码。

代码实现

#include<stdio.h>
//递归实现汉诺塔的交换
//如果只有三个片 且 a b c 中 b 是辅助的：
// 1：a -> c 2：a -> b  3：c -> b  4: a -> c  5:  b -> a   6: b -> c   7: a -> cvoid hanno(int n, char x, char y, char z)
{if (n == 1){printf("把第%d个片从%c放到%c\n", n, x, z);}else{hanno(n - 1, x, z, y);printf("把第%d个片从%c放到%c\n", n, x, z);hanno(n - 1, y, x, z);}
}int main()
{int n = 0;char one = 'A';char two = 'B';char three = 'C';printf("请输入你想要多少个汉诺塔：");scanf("%d", &n);printf("下面就是步骤：\n");hanno(n, one, two, three);
}

代码理解：

 要理解这个问题和代码，你必须对于递归要有一定认识才行，如果不知道，可以看我以往的文章试着理解一下：点这里

 代码验证：

这个代码到底行不行，还是需要通过验证。我们验证的话可以用三个盘子来试试：

三个盘子的话，我们的步骤为：

1： a -> c   2：a -> b  3：c -> b  4: a -> c  5:  b -> a   6: b -> c   7: a -> c

一共七步。

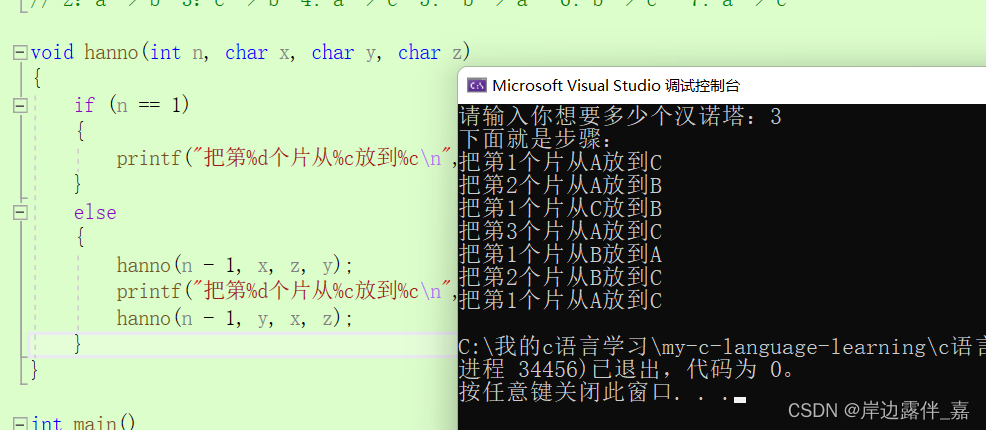
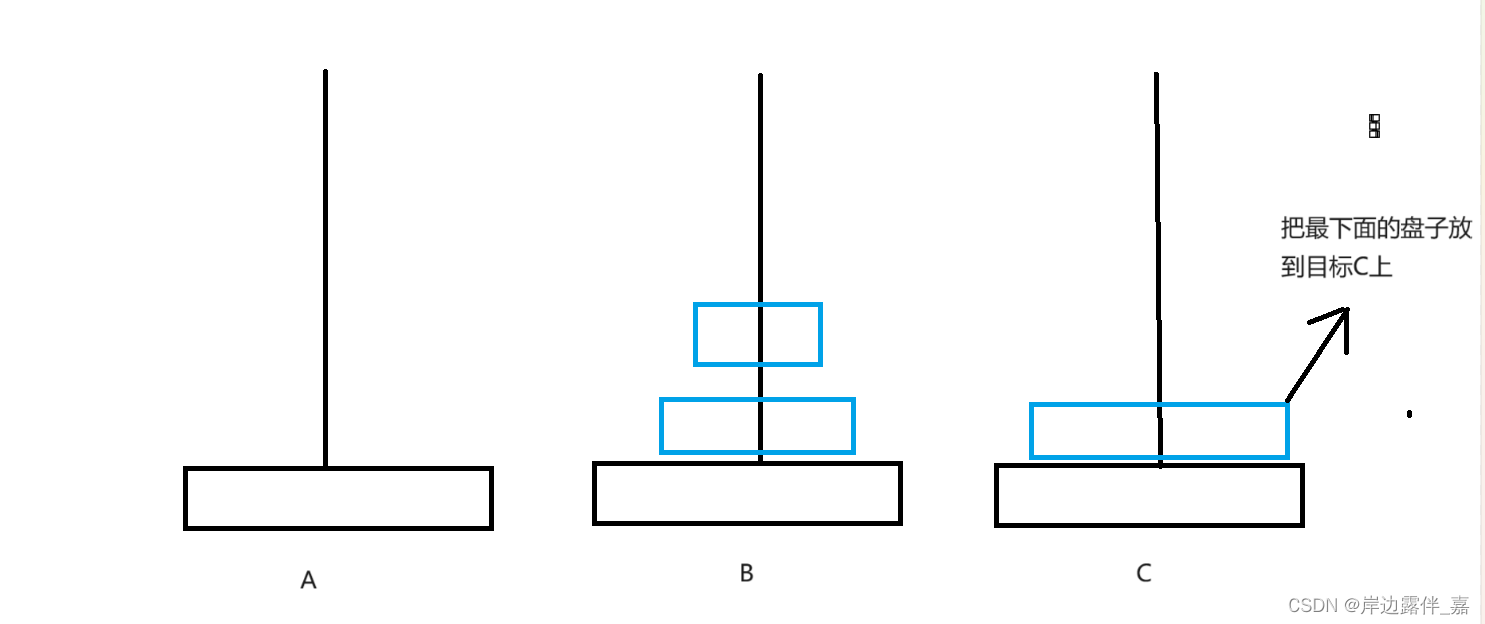
验证下来我们的代码没错，如果还没有懂得代码什么逻辑的，可以一步一步按照逻辑自己看着代码验证一遍，这样就大概率懂得了，类似这样：

当然不一定大家都像我这样理解，只要大家可以懂得方法，自己理解了逻辑就说明都知道了。