2024-6-2，星期日，天气：阴，心情：晴。今天没什么特别的事情发生，心情还是一如既往的好，明天就周一啦，虽然我暂时不用上班，但是希望大家新的一周元气满满~
今日观看了石群老师电路课程的第36和第37个视频，开始了第九章的学习，主要学习内容为：阻抗，RLC串联电路的阻抗，导纳，RLC并联电路的导纳，复阻抗与复导纳的等效互换，并完成了相关定理的推导和例题练习；C语言方面继续学习C Primer Plus第七章内容，并总结C语言笔记。
1. 阻抗
图中，Z为等效阻纳，由下式给出：
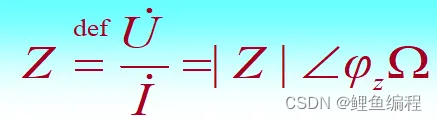
上式也为欧姆定律的向量形式，其中，|Z|=U/I(Ω)称为阻抗模，φz=φu-φi称为阻抗角。当无源网络内部为单个元件时（如图）有：
上面三个式子表明，Z既可以是实数，也可以是虚数。
2. RLC串联电路阻抗
由上式可得，阻抗三角形为：
式中，Z为复阻抗，|Z|为复阻抗的模，φz为阻抗角，R为电阻（阻抗的实部），Z为电抗（阻抗的虚部）。
（1）当ωL>1/ωC，X>0，φz>0时，电路为感性，此时电压超前电流。取电流为参考方向（φi=0），画电压向量图有：
（2）当ωL<1/ωC，X<0，φz<0时，电路为容性，此时电压落后电流。取电流为参考方向（φi=0），画电压向量图有：
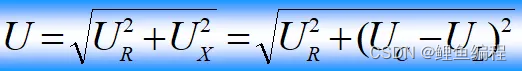
（3）当ωL=1/ωC，X=0，φz=0时，电路为阻性，此时电压电流同向。取电流为参考方向（φi=0），画电压向量图有：
3. 导纳
在正弦稳态情况下，定义导纳为如下形式：
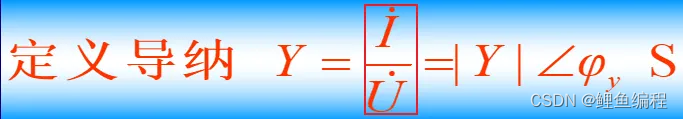式中，|Y|=I/U，称为导纳模；φy=φi-φu，称为导纳角，从上式可以看出，对于同一二端网络有：
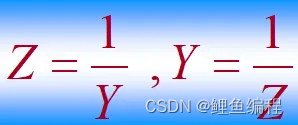
当无源网络内只有一个元件时有：
上面三个式子表明，Y既可以是实数，也可以是虚数
4. RLC并联电路的导纳
由上式可得，导纳三角形为：
式中，Y为复导纳，|Y|为复导纳的模，φY为导纳角，G为电导（导纳的实部），Z为电纳（导纳的虚部）。
（1）当ωC>1/ωL，Y>0，φY>0时，电路为容性，此时电流超前电压。取电压为参考方向（φu=0），画电流向量图有：
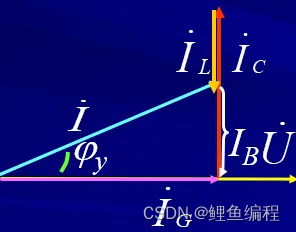
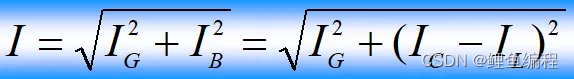
（2）当ωC<1/ωL，Y<0，φY<0时，电路为感性，此时电流落后电压。取电压为参考方向（φi=0），画电流向量图有：
（3）当ωC=1/ωL，Y=0，φY=0时，电路为阻性，此时电压电流同向。取电压为参考方向（φi=0），画电流向量图有：
5.复阻抗与复导纳的等效互换
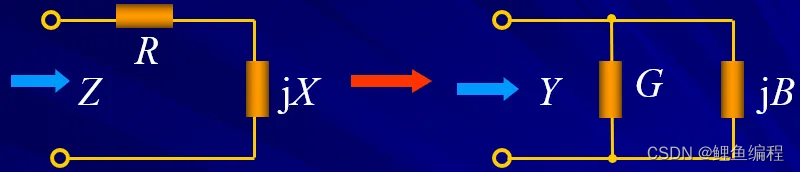
一般情况G≠1/R ，B≠1/X。若Z为感性，X>0，则 B<0，即仍为感性。
同理：
例：
今日总学习时常约5h30min，明日继续学习电路第九章内容，C语言内容，并总结C语言笔记。
