本文讨论的内容参考自《神经网络与深度学习》https://nndl.github.io/ 第7章 网络优化与正则化
网络优化与正则化

网络优化


网络结构多样性

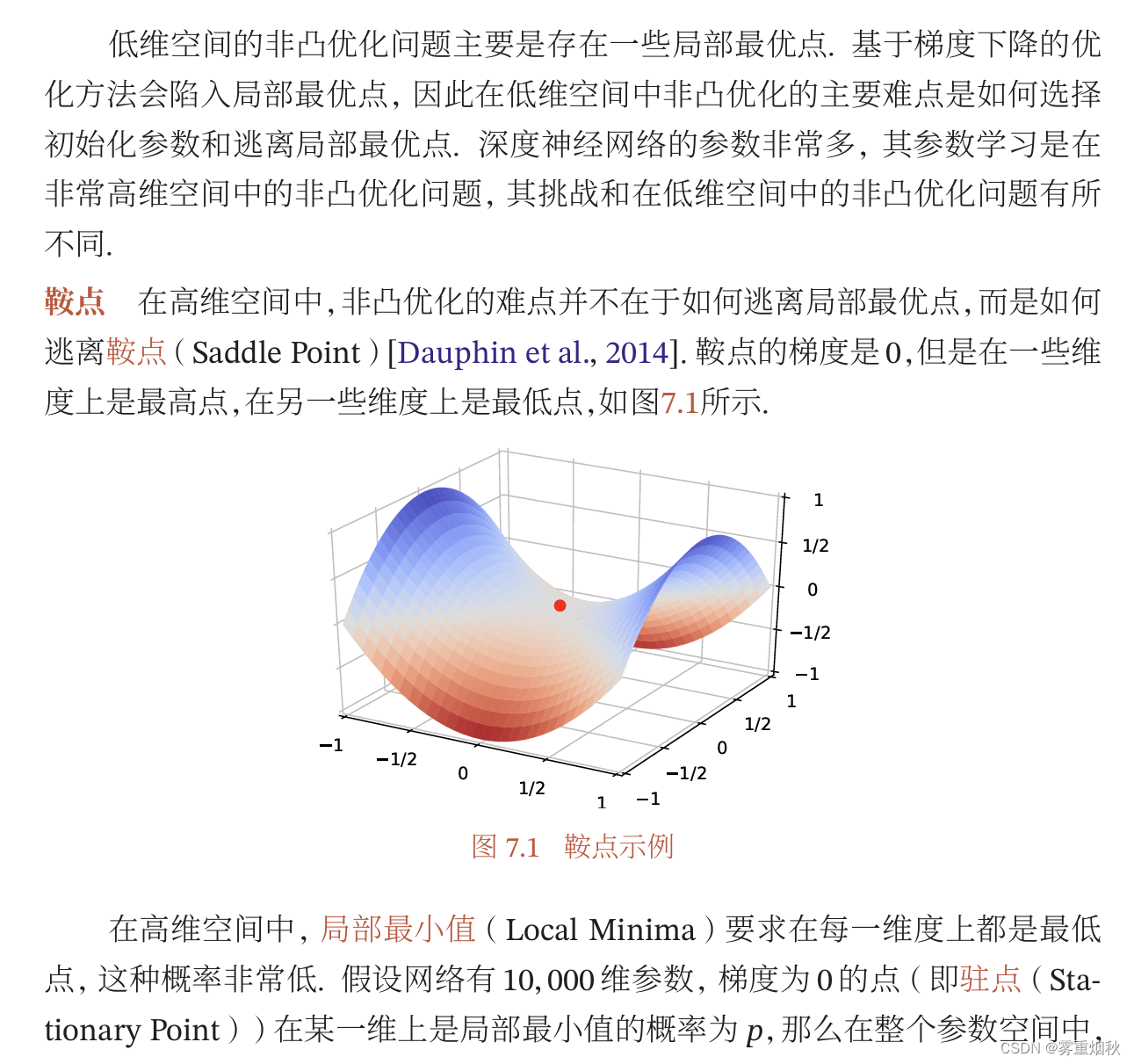
高维变量的非凸优化


神经网络优化的改善方法

优化算法

小批量梯度下降


批量大小选择


学习率调整

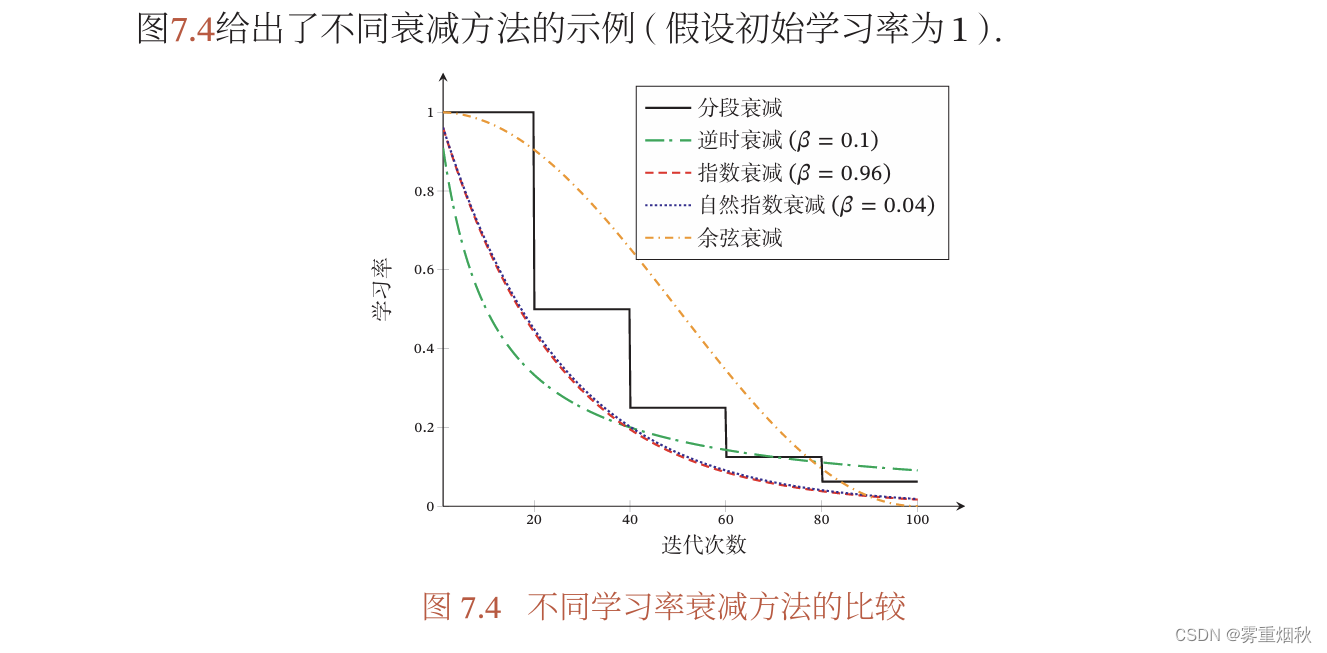
学习率衰减


学习率预热


周期性学习率调整



AdaGrad算法


RMSprop算法

AdaDelta算法


梯度估计修正

动量法


Nesterov加速梯度

Adam算法


梯度截断


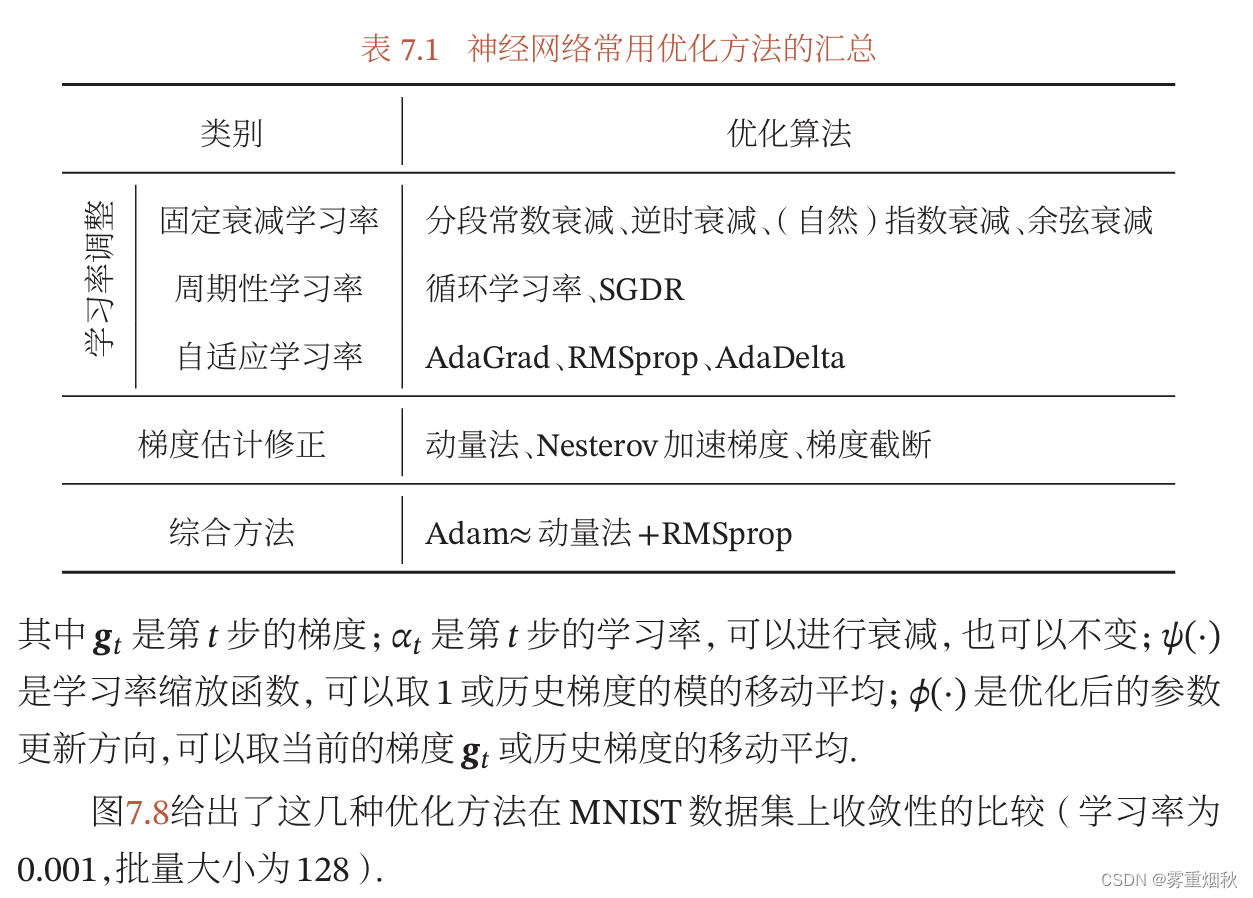
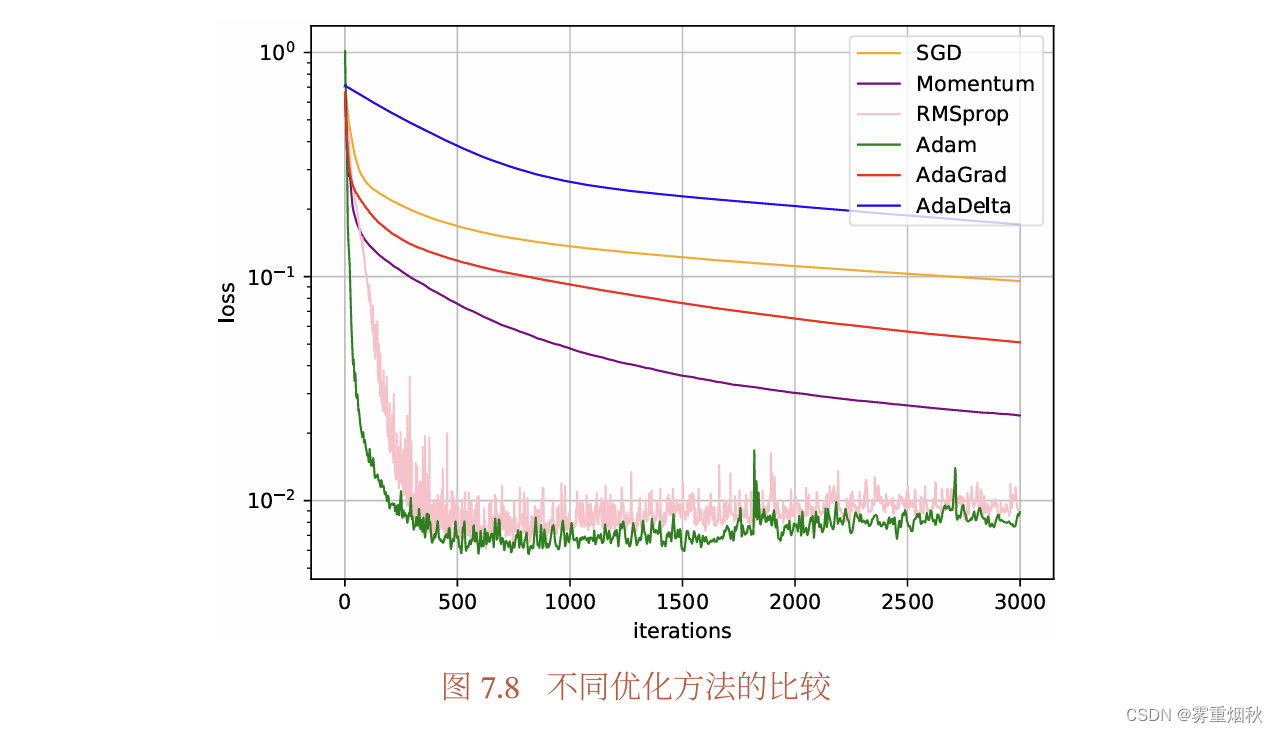
优化算法小结

参数初始化



基于固定方差的参数初始化


基于方差缩放的参数初始化

Xavier初始化



He初始化

正交初始化


数据预处理

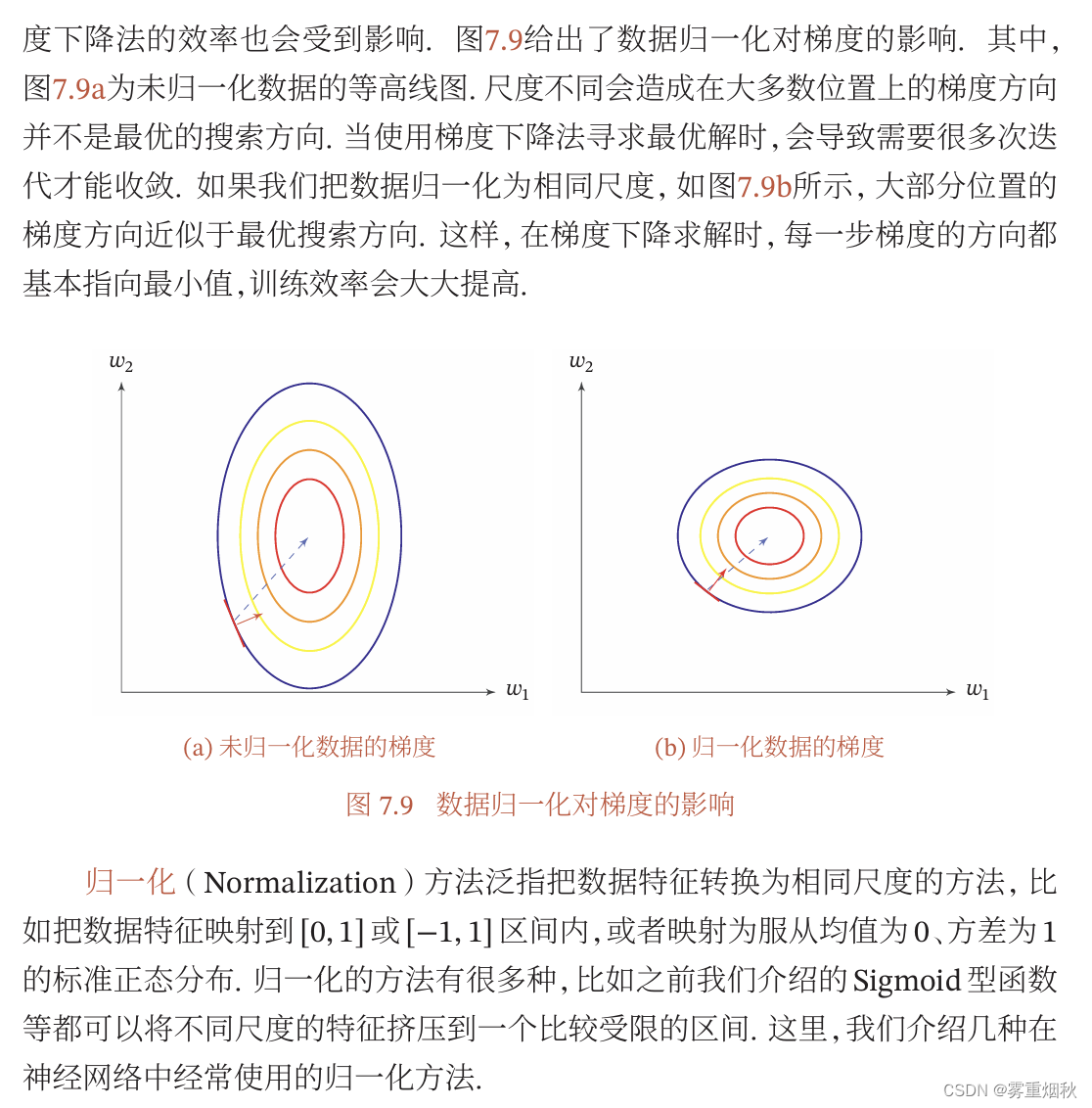

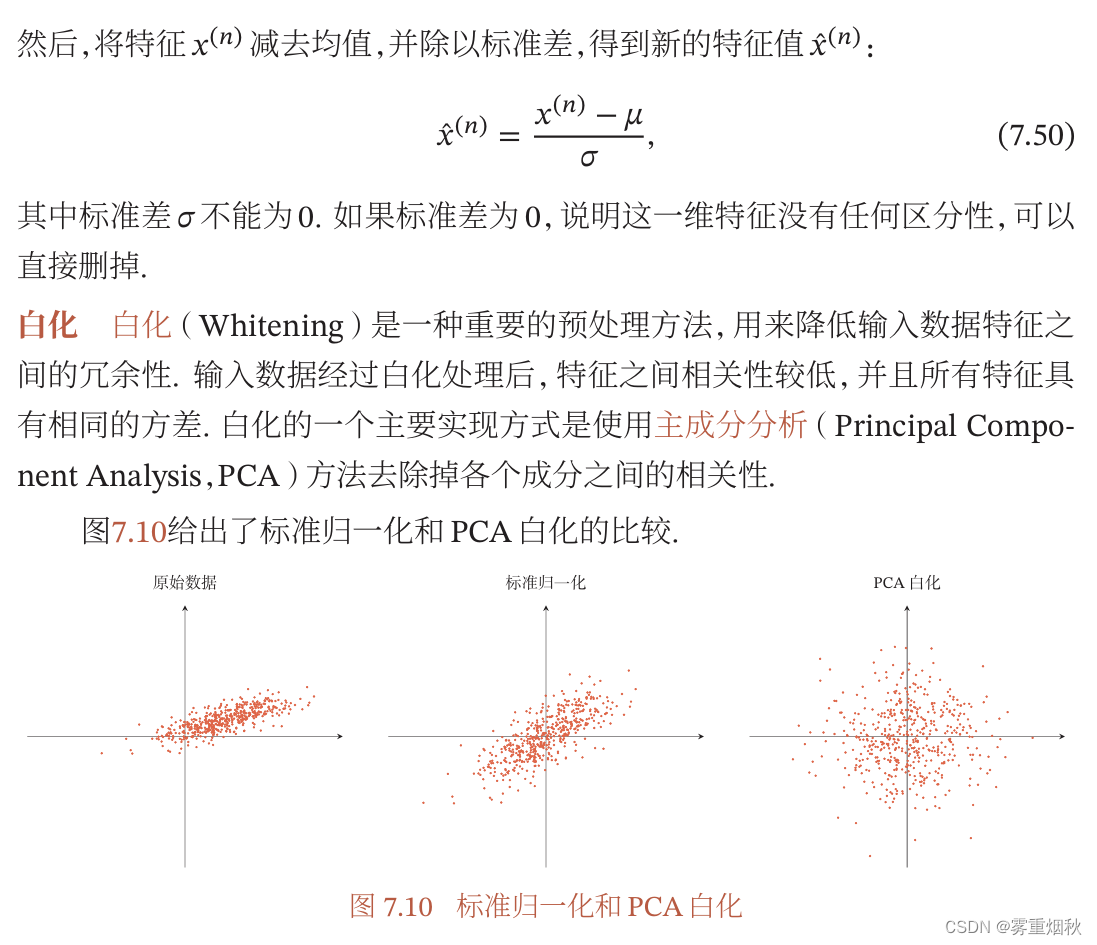
逐层归一化


批量归一化



层归一化


权重归一化

局部相应归一化

超参数优化

网格搜索

随机搜索

贝叶斯优化


动态资源分配


神经架构搜索

网络正则化


l 1 l_1 l1和 l 2 l_2 l2正则化

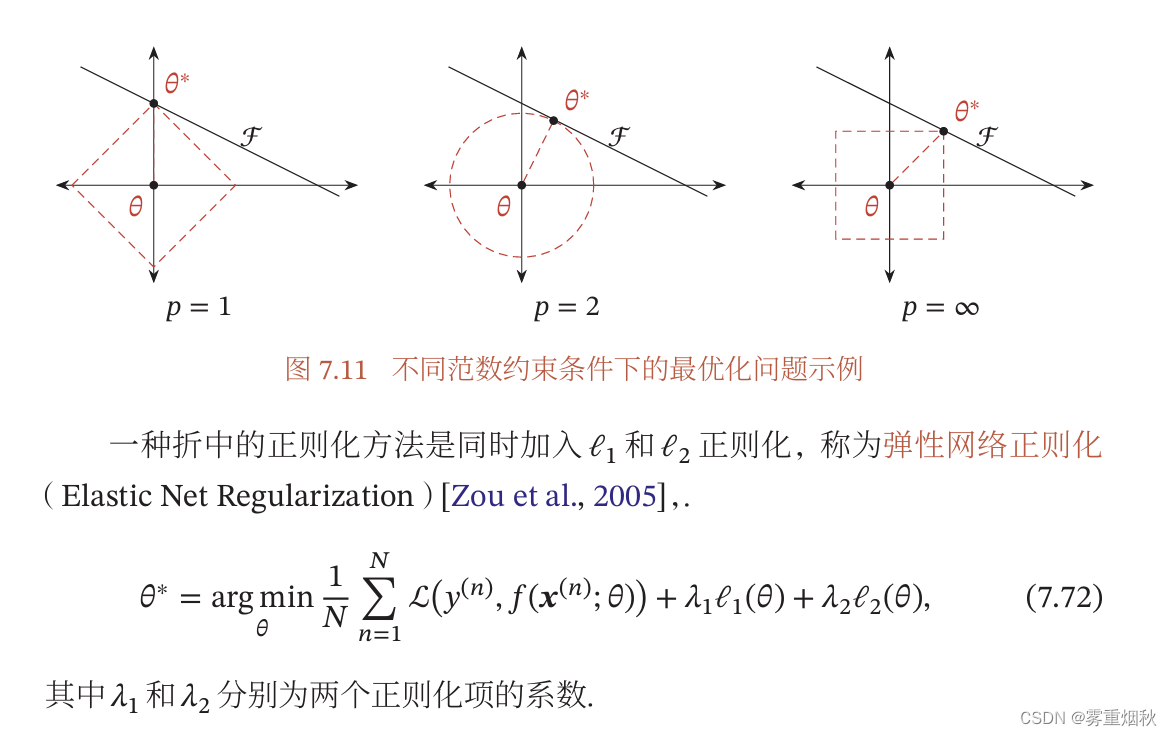
权重衰减

提前停止

丢弃法

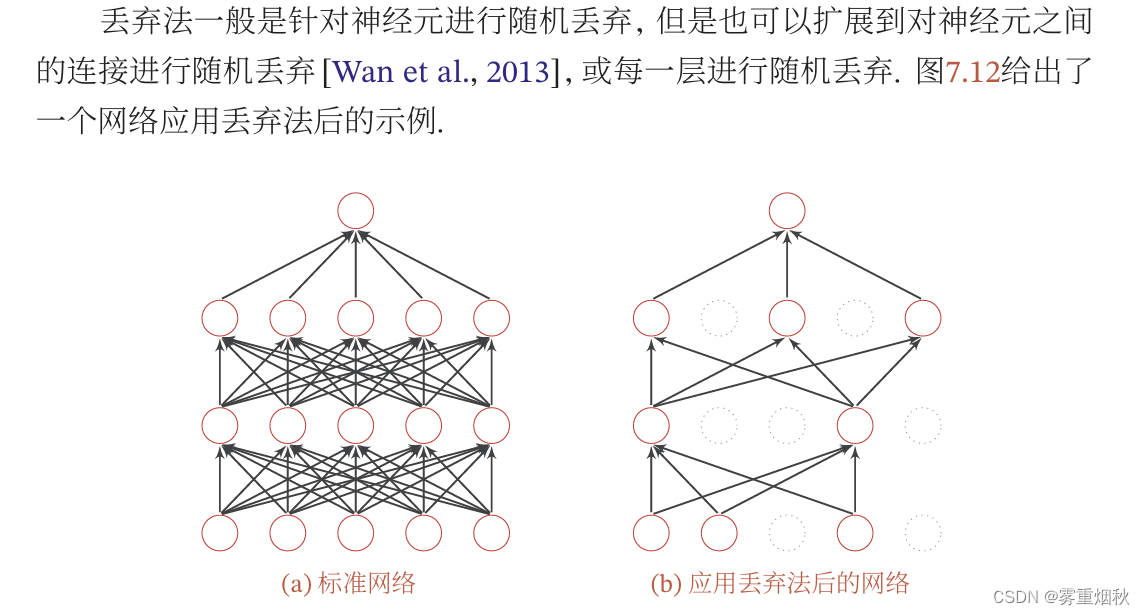

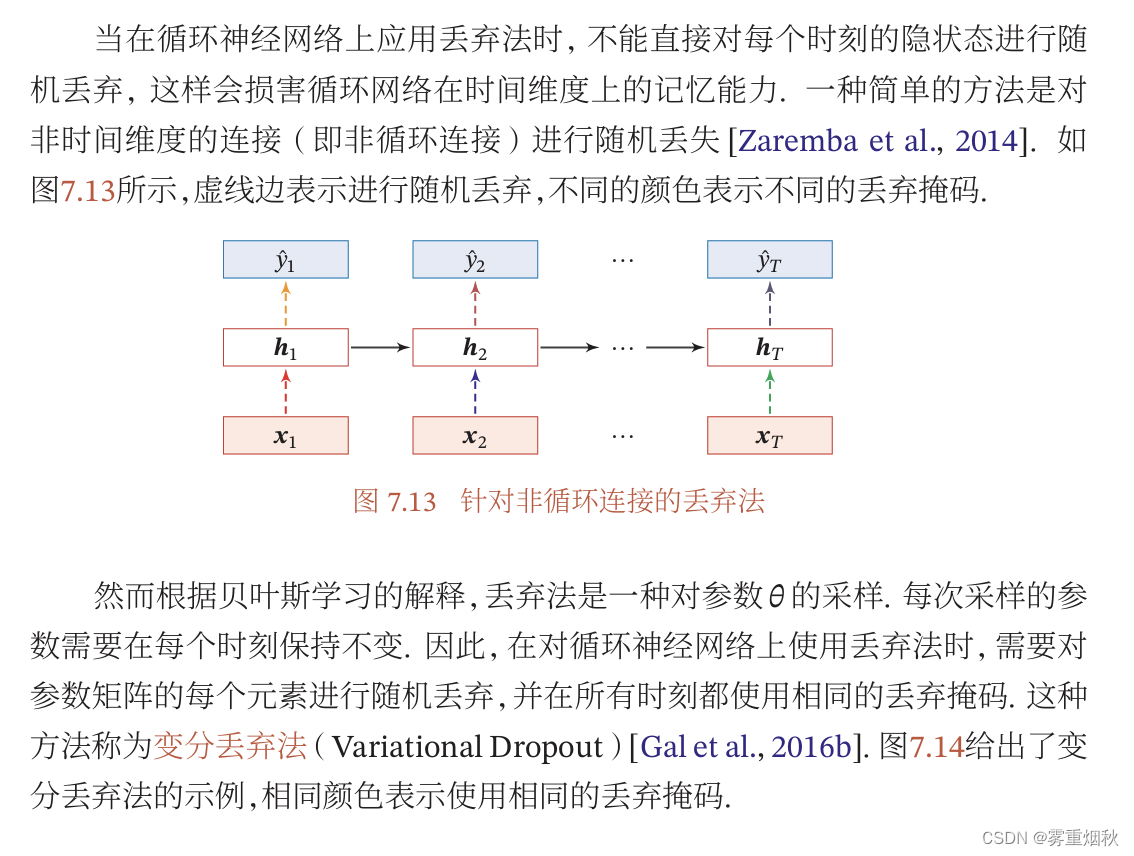
循环神经网络上的丢弃法

数据增强

标签平滑


总结和深入阅读


习题

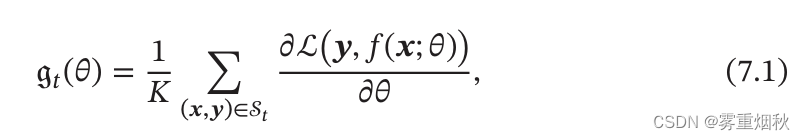
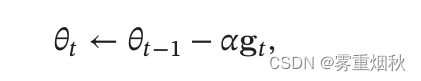
代入可知,KaTeX parse error: Undefined control sequence: \K at position 15: \frac{\alpha}{\̲K̲}可以看作是真正的学习率,如果不成正比,那么会出现过大或者过小的情况,使参数更新不稳定或者过慢。



可以看出,如果 β 1 \beta_1 β1和 β 2 \beta_2 β2都接近1, M ^ t \hat M_t M^t接近 M t M_t Mt, G ^ t \hat G_t G^t接近 G t G_t Gt,当 M 0 = 0 , G 0 = 0 M_0=0, G_0=0 M0=0,G0=0,初期的均值和未减去均值的方差都很大,因为 t t t较小时,由于从0开始增长的很慢,所以基本都趋于0,所以和真实值差距很大,因此需要进行修正, β 1 t \beta^t_1 β1t在 t t t变大的时候越来越趋于0,这样就会使初期的 M t M_t Mt和 G t G_t Gt更新较大,后期更新较小。




AdaDelta算法的 G t G_t Gt计算和RMSprop算法一样,是参数更新差值不同:








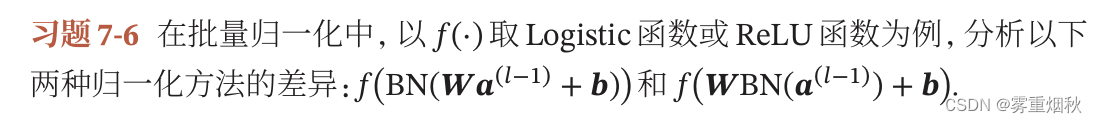

其实就是为了让激活函数 f ( ⋅ ) f(\cdot) f(⋅)的净输入适合激活函数,如果在仿射变换之前进行归一化,那经过了仿射变换以后分布还是变了,可能不适合激活函数的定义域。当用Logistic函数时,如果归一化到[0,1],仿射变换可能让数值大于1,那么梯度就消失了,如果用ReLU函数, x > 0 x > 0 x>0时都是它本身,那么在仿射变换之后可能小于0了,梯度也消失了。

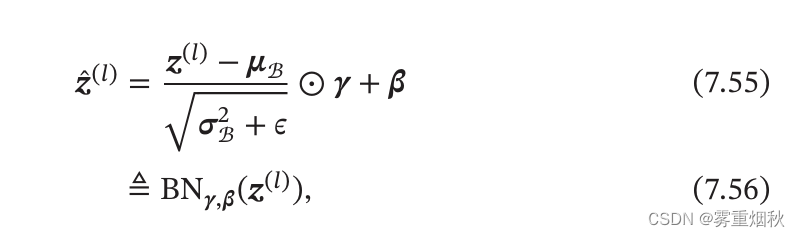
γ \gamma γ和 β \beta β表示缩放和平移的参数向量,通过这两个参数,可以调整输入分布,防止ReLU死亡问题,然后有了 β \beta β的存在,仿射变换就不需要偏置参数。

RNN的梯度随时间反向计算,有一个累积的过程,如果重复进行归一化,会导致梯度爆炸。而且批量归一化是使用小批量的均值和方差来近似整个序列的均值和方差,RNN的序列长度不同,批量均值和方差可能无法反映整个序列的统计特性。批量归一化通常假设批量中的样本是独立同分布的,这和RNN的每一层内不同,RNN的每一层是有时间步的关系。



很明显,对每个时刻的隐藏状态进行随机丢弃,会损坏网络的时间维度上的记忆能力。






)
![[C++] 小游戏 斗破苍穹 2.2.1至2.11.5全部版本(上) zty出品](http://pic.xiahunao.cn/[C++] 小游戏 斗破苍穹 2.2.1至2.11.5全部版本(上) zty出品)

)
】Spring MVC(下))


:@RequestMapping 注解的各种用法)

)





