（2024，LoRA，全量微调，低秩，强正则化，缓解遗忘，多样性）LoRA 学习更少，遗忘更少

LoRA Learns Less and Forgets Less

公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群）

0. 摘要

1. 引言

2. 背景

3. 实验设置

3.2 使用编码和数学基准测试来衡量学习（目标域评估）

3.3 遗忘度量（源域评估）

4. 结果

4.1 在编程和数学任务中，LoRA的表现不如全量微调

4.2 LoRA 的遗忘程度低于全量微调

4.3 学习与遗忘的权衡

4.4 LoRA 的正则化特性

4.5 在代码和数学上的全量微调不学习低秩扰动

4.6 LoRA的最佳配置实用建议

4.6.1 LoRA 对学习率非常敏感

4.6.2 目标模块的选择比秩更重要

6. 讨论

7. 结论

0. 摘要

低秩适配（Low-Rank Adaptation，LoRA）是一种广泛使用的参数高效微调（parameter-efficient fine-tuning）方法，适用于大型语言模型。LoRA 通过仅训练选定权重矩阵的低秩扰动来节省内存。在本研究中，我们比较了 LoRA 和全量微调（full finetuning）在两个目标领域（编程和数学）中的性能。我们考虑了指令微调（≈10 万对提示-响应对）和持续预训练（≈100 亿非结构化标记）这两种数据模式。我们的结果显示，在大多数情况下，LoRA 的性能显著低于全量微调。然而，LoRA 表现出一种理想的正则化形式：它能更好地保持基模型在目标领域之外任务上的性能。我们发现，与常见的正则化技术如权重衰减和 dropout 相比，LoRA 提供了更强的正则化效果；它还有助于保持更多样化的生成结果。我们展示了全量微调学习的扰动，其秩比典型的 LoRA 配置高 10-100 倍，这可能解释了一些报告中的差距。最后，我们提出了使用 LoRA 进行微调的最佳实践建议。

1. 引言

微调具有数十亿参数的大型语言模型（LLM）需要大量的 GPU 内存。参数高效微调方法通过冻结预训练的 LLM，仅训练少量额外的参数（通常称为适配器，adapter）来减少训练期间的内存占用。低秩适配（LoRA；Hu等，2021）训练的是选定权重矩阵的低秩扰动适配器。

自引入以来，LoRA 被宣传为一种严格的效率改进方法，不会在新目标领域上妥协准确性（Hu等，2021；Dettmers等，2024；Raschka，2023；Zhao等，2024b）。然而，只有少数研究将 LoRA 与具有数十亿参数的 LLM 的全量微调进行基准测试（Ivison等，2023；Zhuo等，2024；Dettmers等，2024），且报告的结果喜忧参半。这些研究中有些依赖于较老的模型（例如 RoBERTa）或粗糙的评估基准（如 GLUE 或 ROUGE），这些基准对于当代 LLM 的相关性较低。相比之下，更为敏感的特定领域评估（例如代码）揭示了 LoRA 在某些情况下劣于全量微调（Ivison等，2023；Zhuo等，2024）。在此，我们问：在何种条件下，LoRA 能在代码和数学等具有挑战性的目标领域上接近全量微调的准确性？

通过训练更少的参数，LoRA 被认为提供了一种正则化形式，限制微调模型的行为保持接近基础模型（Sun等，2023；Du等，2024）。我们还问：LoRA 是否作为一种正则化器，减轻了源领域的“遗忘”？

在本研究中，我们严格比较了 LoRA 和全量微调在 Llama-2 7B（在某些情况下是 13B）模型上在代码和数学这两个具有挑战性的目标领域的表现。在每个领域内，我们探索了两种训练模式。

指令微调（instruction finetuning），这是 LoRA 的常见情境，涉及数千万到数亿 token 的问题回答数据集。在这里，我们使用 Magicoder-Evol-Instruct-110K（Wei等，2023）和MetaMathQA（Yu等，2023）。
持续预训练（continued pretraining），这是 LoRA 较少见的应用，涉及数十亿未标记标记的训练；在这里我们使用 StarCoder-Python（Li等，2023）和 OpenWebMath（Paster等，2023）数据集（表 1）。

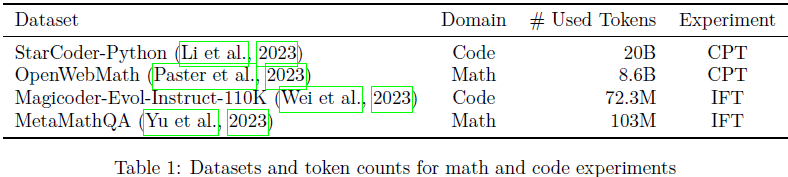
我们通过具有挑战性的编码和数学基准（HumanEval；Chen等，2021和GSM8K；Cobbe等，2021）评估目标领域性能（即学习）。我们通过语言理解、世界知识和常识推理任务（Zellers等，2019；Sakaguchi等，2019；Clark等，2018）评估源领域遗忘性能。我们发现，对于代码，LoRA 的表现显著低于全量微调，而对于数学，LoRA 缩小了更多的差距（第 4.1 节），但需要更长的训练时间。尽管存在性能差距，我们展示了 LoRA 在保持源领域性能方面优于全量微调（第4.2节）。此外，我们刻画了目标域和源域之间性能的权衡（学习与遗忘）。对于给定的模型大小和数据集，我们发现 LoRA 和全量微调形成了相似的学习-遗忘权衡曲线：LoRA 的学习更多时遗忘程度与全量微调相同，尽管我们发现某些情况下（例如代码），LoRA 可以实现类似的学习但遗忘更少（第 4.3 节）。

我们随后展示，即使在较不严格的秩条件下，LoRA 在与经典正则化方法如 dropout（Srivastava等，2014）和权重衰减（Goodfellow等，2016）相比时提供了更强的正则化效果。我们还展示了 LoRA 在输出层面的正则化：我们分析了 HumanEval 问题生成的解决方案，发现全量微调收敛于有限的解决方案集，而 LoRA 保持了与基础模型更为相似的多样化解决方案（Sun等，2023；Du等，2024）。

为什么 LoRA 的表现低于全量微调？LoRA 最初的动机部分是基于这样一个假设：微调会导致基础模型权重矩阵的低秩扰动（Li等，2018；Aghajanyan等，2020；Hu等，2021）。然而，这些研究所探讨的任务对于现代 LLM 来说相对容易，肯定比这里研究的代码和数学领域要容易。因此，我们进行奇异值分解，表明全量微调几乎不改变基础模型权重矩阵的谱，但两者之间的差异（即扰动）是高秩的。随着训练的进行，扰动的秩增长，达到典型 LoRA 配置的 10-100倍（图7）。

我们最后提出了使用 LoRA 训练模型的最佳实践。我们发现 LoRA 对学习率尤其敏感，其性能主要受目标模块的选择影响，秩的影响较小。

总结起来，我们贡献了以下结果：

在代码和数学领域，全量微调在准确性和样本效率上优于 LoRA（第4.1节）。
LoRA 在源领域的遗忘较少，提供了一种正则化形式（第4.2和4.3节）。
LoRA 的正则化效果比常见的正则化技术更强；它还帮助保持生成结果的多样性（第4.4节）。
全量微调找到的是高秩的权重扰动（第4.5节）。
与全量微调相比，LoRA 对超参数（即学习率、目标模块和秩，依次递减）更敏感（第4.6节）。

2. 背景

（2021|ICLR，LoRA，秩分解矩阵，更少的可训练参数）LoRA：大语言模型的低秩自适应

LoRA 涉及冻结预训练的权重矩阵 W_pretrained ∈ R^(d×k)，并仅学习其低秩扰动，这里记作 Δ，如下所示：

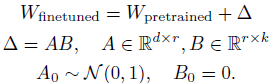
用户选择要适配的 W_pretrained（“目标模块”）和秩 r≪d,k。通过这种方式，仅训练 d×r+r×k 参数，而不是 d×k，从而减少计算梯度所需的内存和浮点运算次数。举个例子，将 r=16 的 LoRA 应用于一个具有 d=k=4096 的 7B 权重矩阵，训练的参数数量不到原始参数数量的 1%。第 D 节列出了 LoRA 的大致内存节省量。

LoRA 还可以通过共享单一基础模型并使用个性化适配器为多个用户提供高效的多租户服务（multi-tenant serving）（Sheng 等，2023）。

在此，我们通过将模块分为三类来简化对目标模块的组合搜索：注意力矩阵

多层感知器（“MLP”）矩阵

以及 “All”——它们的并集，适用于 L 层。需要注意的是，尽管在原始研究中 LoRA 仅应用于注意力矩阵（Hu 等，2021），但目前的标准是针对更多的模块（Raschka，2023；Dettmers 等，2024）。

3. 实验设置

3.2 使用编码和数学基准测试来衡量学习（目标域评估）

编码 - HumanEval。这个基准测试（Chen等，2021）包含了 164 个问题，涉及根据文档字符串和函数签名生成 Python 程序。如果生成的程序通过了所有提供的单元测试，则认为生成是正确的。我们使用代码生成 LM 评估工具（Ben Allal等，2022），配置为每个问题输出 50 个生成结果，使用 softmax 温度为 0.2 进行采样，并计算 “pass@1”。

数学 - GSM8K。这个基准测试（Cobbe等，2021）包含了 8500 个小学数学单词问题。我们在 GSM8K 的测试集上进行评估（1319 个样本），采用 LM 评估工具（Gao等，2023）中的默认生成参数（温度=0，5 few-shot，pass@1）。

3.3 遗忘度量（源域评估）

HellaSwag。这个基准测试（Zellers等，2019）包含了 70,000 个问题，每个问题描述了一个事件，并有多种可能的延续。任务是选择最合理的延续，这需要对微妙的日常情况进行推理。

WinoGrande。这个基准测试（Sakaguchi等，2019）也评估了常识推理能力。它包括 44,000 个句子问题，需要解决歧义代词的问题。

ARC-Challenge。这个基准测试（Clark等，2018）包含了 7,787 个小学级别的多项选择科学问题，测试了复杂推理和科学概念理解的能力。

4. 结果

4.1 在编程和数学任务中，LoRA的表现不如全量微调

在图 2 中，我们总结了六个 LoRA 模型在每个训练时长下的最小、平均和最大性能（以紫色表示），并将它们与全量微调（实线黑色）和基础模型（虚线水平线）进行比较；结果在图 S2 中进一步按 LoRA 配置细分。首先需要注意的是，对于这两个领域，指令微调（IFT）相比持续预训练（CPT）带来了更显著的改进，这是预料之中的，因为 IFT 的问题更类似于评估问题（例如，对于代码，IFT 的最高 HumanEval 得分为 0.50，而 CPT 为 0.26）。

对于代码 CPT（图 2A），我们发现全量微调与 LoRA 之间的差距随着数据量的增加而扩大。整体上，表现最好的 LoRA 在 16B tokens 时达到峰值（rank=256，“All”），HumanEval 得分为0.175，大致相当于全量微调在 1B tokens 时的表现（HumanEval=0.172）。全量微调在 20B tokens 时达到其最高 HumanEval 得分 0.263。对于代码 IFT（图 2B），表现最好的 LoRA（r = 256，“All”）在第 4 个 epoch 时达到 HumanEval 得分 0.407，显著低于全量微调在第 2 个 epoch 时的 HumanEval 得分 0.464 和其在第 8 个 epoc h时的最高 HumanEval 得分 0.497。

数学 CPT（图2C）的结果显示，训练 1B tokens 或更少会使 GSM8K 结果低于基线（GSM8K=0.145）。随着数据量的增加，性能有所提升，表现最好的 LoRA（rank=256，“All”）在 8.6B tokens 时达到 GSM8K 得分 0.187，低于全量微调在 4.3B tokens 时的 GSM8K 得分 0.191 和在 8.6B tokens 时的 GSM8K 得分 0.230。在数学 IFT（图2D）数据集中，LoRA 在大多数情况下缩小了与全量微调的差距。然而，LoRA 仍然不如全量微调高效。LoRA（r = 256，“All”）在第 4 个 epoch 时达到峰值（GSM8K=0.622），而全量微调在第 2 个 epoch 时达到 GSM8K 得分 0.640 并在第 4 个 epoch 时达到峰值 GSM8K 得分 0.642。两种方法的性能均大大超过了基础模型。我们推测，这里的差距较小可能对应于数学问题与预训练数据之间的领域转变较小，不同于代码中的较大转变。

总之，跨 LoRA 配置和训练时长来看，LoRA 的表现仍然不如全量微调。这些效果在编程领域比在数学领域更为显著。对于这两个领域，指令微调比持续预训练带来了更大的准确性提升。

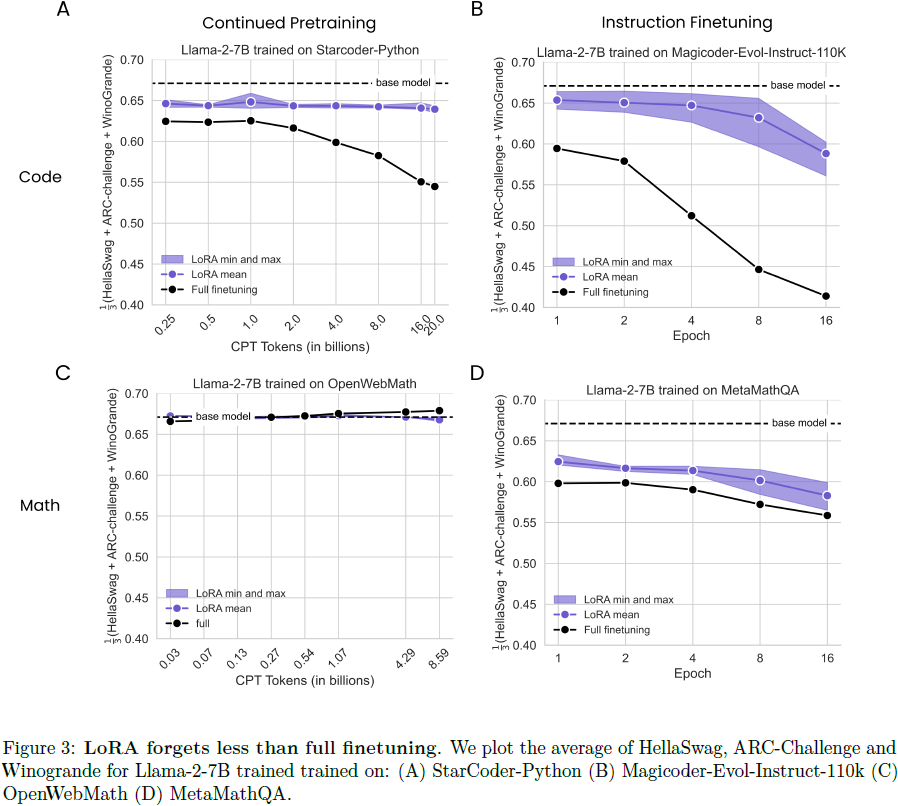
4.2 LoRA 的遗忘程度低于全量微调

我们将遗忘定义为 HellaSwag、ARC-challenge 和 WinoGrande 基准测试平均成绩的下降，并在图 3 中探讨其随数据量的变化。总体而言，我们观察到以下几点：(1) 指令微调（IFT）比持续预训练（CPT）引起更多的遗忘，(2) 编程引起的遗忘比数学更多，(3) 遗忘随着数据量的增加而增加。最重要的是，LoRA 的遗忘程度低于全量微调，且如 4.1 中所述，这种效果在编程领域更加显著。在代码 CPT 中，LoRA 的遗忘曲线大致保持不变，而全量微调的性能随着数据量增加而下降（在 HumanEval 达到峰值时的遗忘指标：全量微调在 20B tokens 时为 0.54，LoRA 在 16B tokens 时为 0.64）。在编程 IFT 中，两种方法在训练更多 epochs 时都出现了性能下降，在其峰值性能（4 和 8 个 epochs）时，LoRA 的得分为 0.63，而全量微调的得分为 0.45。

对于数学任务，在 OpenWebMath CPT 数据集中没有明显的趋势，LoRA 和全量微调均未表现出遗忘。这可能是因为 OpenWebMath 数据集中以英语句子为主，而 StarCoder-Python 数据集则以 Python 代码为主（详见 3.1）。在数学IFT中，LoRA的遗忘程度再次低于全量微调（在第 4 个 epoch 时分别为 0.63 和 0.57）。

4.3 学习与遗忘的权衡

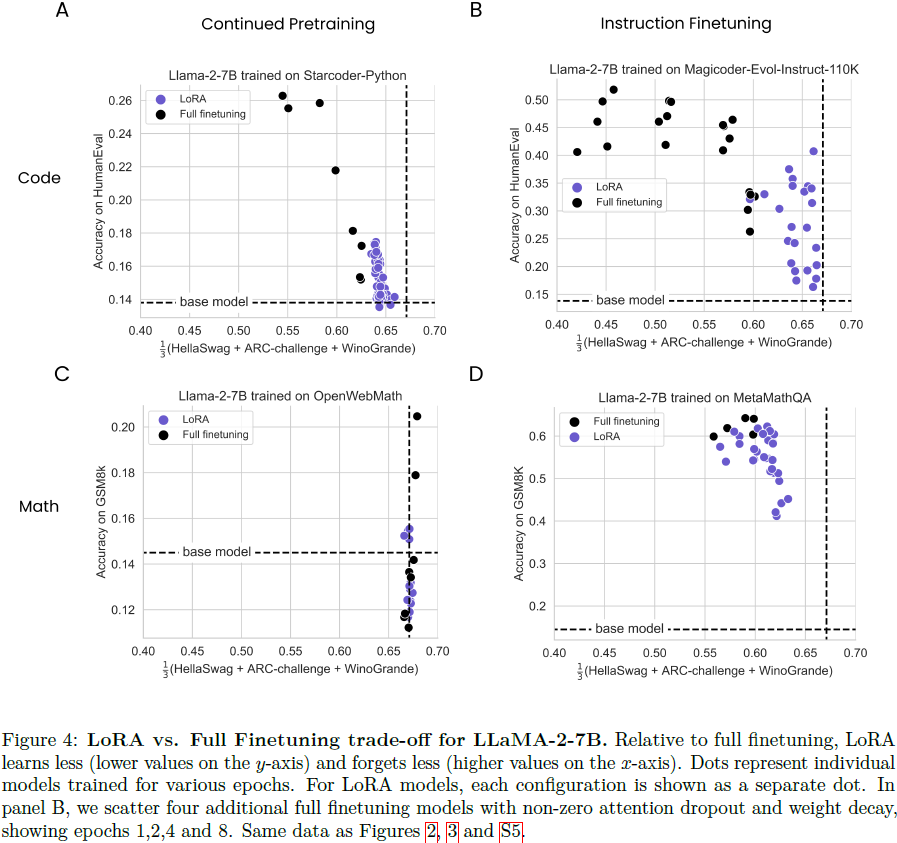
显然，模型在微调到新的目标领域时改变越少，就会遗忘源领域的内容越少。非平凡的问题是： LoRA 和全量微调在如何权衡学习和遗忘方面有何不同？LoRA 能否实现类似的目标域性能，但遗忘减少？

我们通过绘制遗忘指标与学习指标（GSM8K 和 HumanEval）的聚合曲线来形成一个学习-遗忘帕累托曲线，在这个空间中，不同模型（在不同训练时长下训练）分布为点（图 4）。LoRA 和全量微调似乎占据同一帕累托曲线，LoRA 模型位于右下方 - 学习和遗忘都更少。然而，我们能够找到一些情况，特别是对于代码 IFT，LoRA 在具有可比目标域性能水平时，表现出更高的源域性能，呈现出更好的权衡。在补充图 S5 中，我们展示了每个模型的原始评估分数。在补充图 S3 中，我们将 Llama-2-13B 结果与 Llama-2-7B 的结果在代码 CPT 中绘制在同一图中。

4.4 LoRA 的正则化特性

在这里，我们将正则化（宽泛地）定义为一种训练机制，使微调后的 LLM 保持与基础 LLM 相似。我们首先分析学习-遗忘权衡中的相似性，然后分析生成的文本。

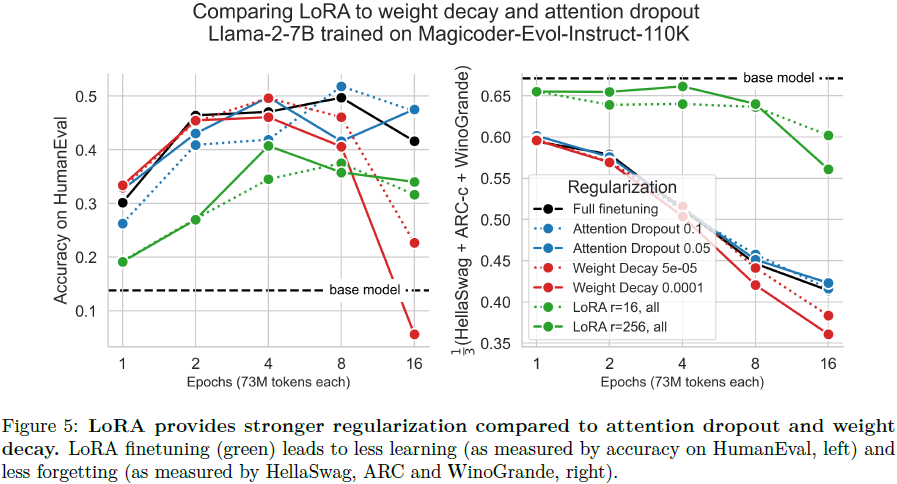
与权重衰减（weight decay）和注意力丢弃（dropout）相比，LoRA 是一种更强的正则化方法。我们使用在 Magicoder-Evol-Instruct-110K 数据集上训练的 Llama-2-7B 模型，并将 LoRA（r = 16, 256，“All”）与权重衰减（Goodfellow等，2016）和注意力丢弃（Srivastava等，2014）进行比较，权重衰减的值为 5e−5、1e−4，注意力丢弃的值为 0.05、0.1。我们发现 LoRA 提供了更强的正则化：它学习和遗忘更少。

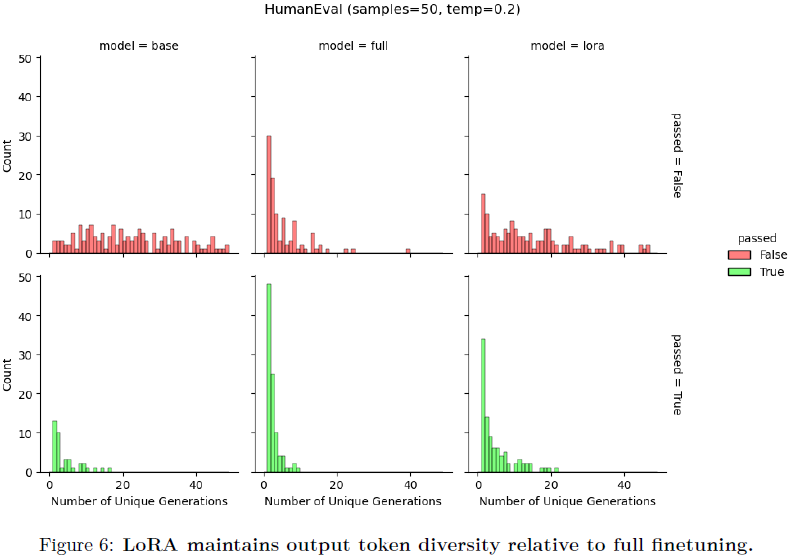
LoRA 有助于保持标记生成的多样性。我们再次使用在 Magicoder-Evol-Instruct-110K 数据集上训练的 Llama-2-7B 模型，来审查 HumanEval 期间生成的字符串。我们计算了每个模型的 50 个生成中的独特字符串数量，作为预测多样性的粗略代理。在图 6 中，我们分别展示了正确和错误答案的结果。正如在来自人类反馈的强化学习文献中所提到的（Du等，2024；Sun等，2023），我们发现全量微调导致的独特生成数量较少（“分布崩溃”），与基础模型相比，无论是通过还是失败的生成都是如此。我们发现 LoRA 在两者之间提供了一种折衷，就生成水平而言。以上工作还表明，LoRA 甚至可以替代一个常见的正则化项，使得微调后的生成文本的概率与基础模型保持相似。

4.5 在代码和数学上的全量微调不学习低秩扰动

在本节中，我们试图研究是否应该预期低秩训练是对全量微调的良好近似，并且如果是这样，必要的秩是多少。回想一下，全量微调可以写成 W_finetuned = W_pretrained + Δ；在这里，我们计算方程中所有三个项的奇异值分解。我们专注于代码的持续预训练，在 LoRA 和全量微调之间存在巨大差异。我们分析了在 0.25、0.5、1、2、4、8、16 和 20 亿训练 token 时获得的检查点。

首先，在补充图 S6 中，我们展示了 Llama-2-7B（维度为4096×4096）第 26 层的 W_q 投影的结果。我们显示，微调后的权重矩阵的谱与基础权重矩阵的谱非常相似，两者都缓慢衰减，并且需要保留 ≈50% 的奇异向量（≈2000/4096）来解释权重矩阵中 90% 的方差。关键是，差异 Δ 的谱与微调后的以及基础权重矩阵的谱也非常相似（多个因子的缩放）。我们认为，全量微调谱没有什么特别之处；通过向权重矩阵添加低幅度的高斯独立同分布噪声，可以实现类似的谱（图 S7）。

接下来，我们询问在训练过程中，扰动何时变为高秩，并且在模块类型和层之间是否有意义地变化。我们估计解释矩阵中 90% 方差所需的秩。结果见图 7。我们发现：（1）在 0.25B CPT token 处的最早检查点显示 Δ 矩阵的秩比典型的 LoRA 秩大 10-100倍；（2）当使用更多数据进行训练时，Δ 的秩会增加；（3）MLP 模块的秩比注意力模块高；（4）第一层和最后一层的秩似乎比中间层低。

4.6 LoRA的最佳配置实用建议

尽管优化 LoRA 超参数无法弥补与全量微调之间的差距，但我们在下面强调一些超参数选择比其他超参数更有效的情况。

4.6.1 LoRA 对学习率非常敏感

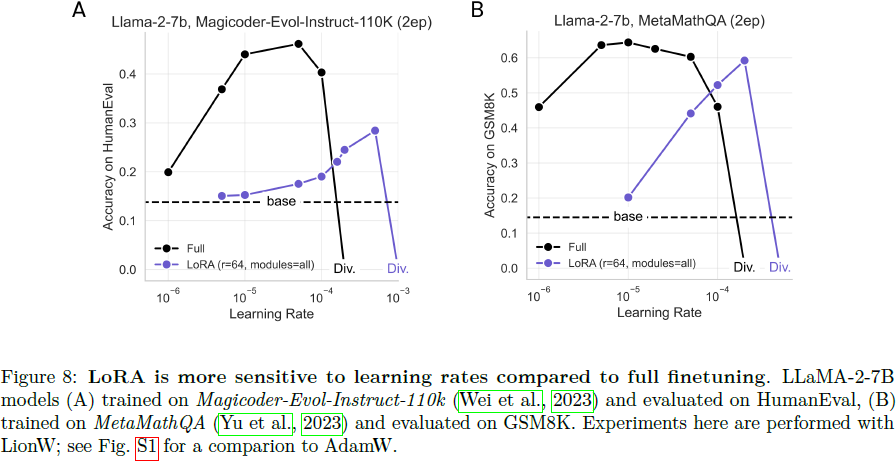
我们对 Llama-2-7B 进行了学习率敏感性分析，它们在代码和数学 IFT 数据集上训练了两个周期，然后分别进行了 HumanEval 和 GSM8K 评估。对于 LoRA，我们将 r = 64，目标模块设置为“All”。图 8 显示，LoRA 随着学习率的增加而单调改善，直到训练发散，最佳学习率分别为 5e−4 和 2e−4，分别用于代码和数学。在这两个数据集上，这些最佳 LoRA 学习率都被四种备选全量微调学习率表现。最佳全量微调学习率分别为 5e−5 和 1e−5，比 LoRA 小一个数量级。对于 LoRA，我们找不到能够达到最佳学习率性能 90% 的替代学习率。对于全量微调，代码和数学分别有两种可行的替代学习率。

4.6.2 目标模块的选择比秩更重要

有了最佳学习率后，我们继续分析秩（r = 16, 256）和目标模块的影响。我们发现 “All” > “MLP” > “Attention”，尽管秩的影响更轻微，r = 256 > r = 16。因此，我们得出结论，针对 “All” 模块选择相对较低的秩（例如，r = 16）提供了性能和准确性之间的良好平衡。

总的来说，我们建议将 LoRA 用于 IFT 而不是 CPT；确定能够实现稳定训练的最高学习率；针对 “All” 模块进行目标设置，并根据内存约束选择秩，16 是一个不错的选择；探索至少进行四个周期的训练。

6. 讨论

LoRA 和全量微调之间的差异是否随着模型大小的增加而减小？过去的研究曾暗示了微调效果和模型大小之间的关系。虽然最近的研究已成功地将 LoRA 应用于 70 亿参数模型，但我们将对这些有趣的扩展性属性进行严格的研究留给未来的工作。

谱分析的局限性。全量微调倾向于找到高秩解决方案并不排除低秩解决方案的可能性；相反，它显示通常找不到低秩解决方案。另一种解释是，重构权重矩阵所需的秩高于下游任务所需的秩。

为什么 LoRA 在数学上表现良好而在编码上表现不佳？一个假设是数学数据集涉及的领域变化较小；它们包含的英语比例较大，并导致遗忘减少。第二个假设是 GSM8K 评估过于简单，无法捕捉到微调中学到的新的大学水平数学知识。

7. 结论

本文阐明了使用 LoRA 训练的当代 LLM（具有 70 亿和 130 亿参数）在下游任务中的表现。与大多数先前的工作不同，我们在代码和数学领域使用了特定领域的数据集，并使用了敏感的评估指标。我们展示了 LoRA 在两个领域中表现不及全量微调。我们还展示了 LoRA 使微调模型的行为保持接近基础模型，避免了源域的遗忘，并在推理时生成更多样化的结果。我们调查了 LoRA 的正则化属性，并展示了全量微调找到的权重扰动远非低秩。最后，我们分析了 LoRA 对超参数的敏感性，并强调了最佳实践。