目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.背景
2024年,H Zhang受到雷达技术启发,提出了波搜索算法(Wave Search Algorithm, WSA)。


2.算法原理
2.1算法思想
WSA模拟雷达工作时的发射、反射和接收波的过程,并且利用了被优化问题的梯度信息,采用了多种改进的贪心机制,具有准确、高效、灵活、适应性强的特点。
2.2算法过程
初始化
首秀按准备n个随机数k1, k2…Kn(0<Ki<1),初始化粒子位置:
x i = ∑ 1 i k i / ∑ 1 n k i (1) x_i=\sum_1^ik_i/\sum_1^nk_i\tag{1} xi=1∑iki/1∑nki(1)
其中xi为均匀化ki, x * 为x中的随机值:
W = l b + x ∗ ( u b − l b ) (2) W=lb+x^*\left(ub-lb\right)\tag{2} W=lb+x∗(ub−lb)(2)
全局探索
W i n e w = W m i n + r 1 ⋅ ( W m a x − W m i n ) { W i = W i n e w i f f ( W i n e w ) ≤ f m e a n W i = W i i f f ( W i n e w ) > f m e a n (3) W_{i}^{new}=W_{\mathrm{min}}+r_{1}\cdot(W_{\mathrm{max}}-W_{\mathrm{min}})\\\\\left\{\begin{array}{ll}W_i=W_i^{new}&if&f\left(W_i^{new}\right)\leq f_{mean}\\W_i=W_i&if&f\left(W_i^{new}\right)>f_{mean}\end{array}\right.\tag{3} Winew=Wmin+r1⋅(Wmax−Wmin){Wi=WinewWi=Wiififf(Winew)≤fmeanf(Winew)>fmean(3)
其中,Wmin是由W各维上的最小值组成的向量,Wmax是由W各维上的最大值组成的向量,fmean是所有粒子适应度值的平均值。此策略可以逐步缩小搜索范围,新生成的点在缩小的范围内生成,提高了搜索效率,采用贪婪机制控制种群在全局最优位置附近的位置。
局部开发
发送电磁波
模拟电磁波向外扩散,减少陷入局部最优的可能性,提高搜索效率。
W i n e w = W b e s t + ( W l i − W b e s t ) ⋅ ( 1 + m i ) σ (4) W_i^{new}=W_{best}+\frac{(W_{l i}-W_{best})\cdot(1+m_i)}{\sigma}\tag{4} Winew=Wbest+σ(Wli−Wbest)⋅(1+mi)(4)
其中,σ为波形大小控制系数,表述为:
σ = − ( 5 t / T − 2 ) / 25 ( 5 t / T − 2 ) 2 + 0.7 (5) \sigma=-(5t/T-2)/\sqrt{25{\left(5t/T-2\right)}^{2}}+0.7\tag{5} σ=−(5t/T−2)/25(5t/T−2)2+0.7(5)
反射电磁波
g i = ( f ( W + ε i ) − f ( W − ε i ) ) / 2 ε W i = W i − α ⋅ g i (6) g_{i}=\left(f\left(W_{+\varepsilon i}\right)-f\left(W_{-\varepsilon i}\right)\right)/2\varepsilon\\W_{i}=W_{i}-\alpha\cdot g_{i}\tag{6} gi=(f(W+εi)−f(W−εi))/2εWi=Wi−α⋅gi(6)
其中W εi = Wi ε, W−εi = Wi−ε, ε = 10−6,g为梯度,α为阶跃系数,α的初始值设为0.45。步长试验方法如下:如果初始步长迭代后的适应度值小于等于当前适应度值,则α = 1.5α,否则α = 0.5α。此策略采用中心差分法求解待优化问题的解析信息,用于搜索最优解。
接收电磁波
{ W i n e w = W i + δ ⋅ r 2 ⋅ ( W b e s t − W i ) + η ⋅ cos ( π i n ) ⋅ ( W b e s t − W i ) i f r 5 ≤ 0.7 W i n e w = W i + λ ⋅ r 3 ⋅ ( W b e s t − W i ) + 0.5 ⋅ r 4 ⋅ ( 1 − λ ) ⋅ ( W b e s t ∗ − W i ) i f r 5 > 0.7 (7) \left\{\begin{array}{ll}W_i^{new}=W_i+\delta\cdot r_2\cdot(W_{best}-W_i)+\eta\cdot\cos(\frac{\pi i}{n})\cdot(W_{best}-W_i)&if r_5\leq0.7\\W_i^{new}=W_i+\lambda\cdot r_3\cdot(W_{best}-W_i)+0.5\cdot r_4\cdot(1-\lambda)\cdot(W_{best}^*-W_i)&if r_5>0.7\end{array}\right.\tag{7} {Winew=Wi+δ⋅r2⋅(Wbest−Wi)+η⋅cos(nπi)⋅(Wbest−Wi)Winew=Wi+λ⋅r3⋅(Wbest−Wi)+0.5⋅r4⋅(1−λ)⋅(Wbest∗−Wi)ifr5≤0.7ifr5>0.7(7)
其中δ是接受系数,表述为:
δ = 0.6 + ( 1.2 − 0.5 ) sin ( t π 2 T ) (8) \delta=0.6+(1.2-0.5)\sin(\frac{t\pi}{2T})\tag{8} δ=0.6+(1.2−0.5)sin(2Ttπ)(8)
伪代码

3.结果展示
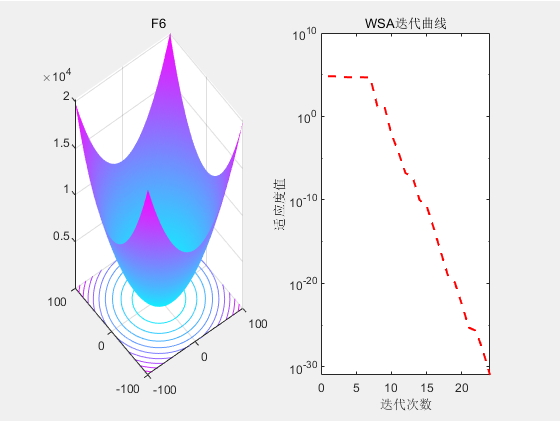

4.参考文献
[1] Zhang H, San H, Sun H, et al. A novel optimization method: wave search algorithm[J]. The Journal of Supercomputing, 2024: 1-36.
5.代码获取
资源清单








)









)
