支持向量机

• 概念

  是supported vector machine（支持向量机），即寻找一个超平面使样本分成两类，且间隔最大分类

• 分类

  • 硬间隔

    • 若样本线性可分，且所有样本分类正确情况下，寻找最大间隔，即硬间隔

    • 若出现异常值或样本不能线性可分，则无法实现

  • 软间隔

    • 允许部分样本，在最大间隔之间，甚至在错误的一边，寻找最大间隔，即软间隔

    • 目标是尽可能保持间隔宽阔和限制间隔违例之间找到良好平衡

• 核函数Kernel

  将原始输入空间映射到新的特征空间，使得原本线性不可分样本在核空间可分

SVMAPI

• class sklearn.svm.LinearSVC(C=1)

• C：惩罚参数，类似于线性回归中正则化系数

• LinearSVC API使用方法

  • 导包：from sklearn.svm import LinearSVC

  • 实例化： mysvc = LinearSVC(C=30)

  • 训练模型：mysvc.fit(X_standard,y)

  • 输出准确率：print(myscv.score(X_standard,y))

• 惩罚参数C对超平面影响

  C值越大，间隔越小，落在间隔中的违例越少，反之，C值越小，间隔越大，违例越多

SVM算法原理

• 思想：要去求一组参数(w,b)，使其构建的超平面函数能够最优分离两个集合

• 样本空间中任意点x到超平面(w,b)距离可为：

  

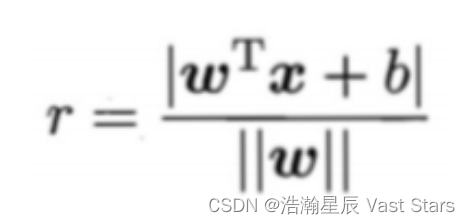
• 若想找到具有最大间隔划分超平面，也就是要找到能满右足式中约束参数w和b，使得间隔γ最大

  

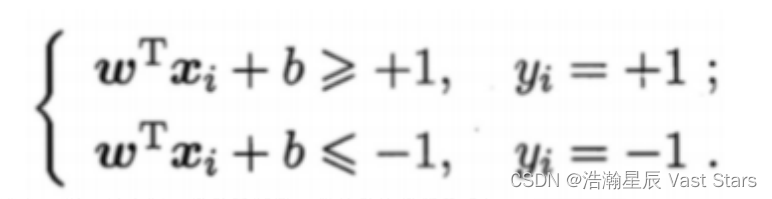
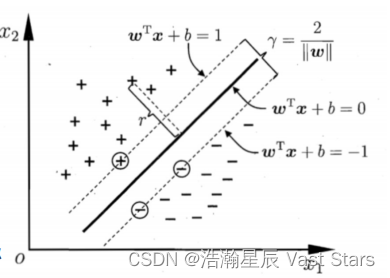
• 距离超平面最近的几个训练样本点使上式等号成立，他们被称为“支持向量”两个异类支持向量到超平面距离之和为：

  

SVM核函数

• 作用

  将原始输入空间映射到新的特征空间，从而使原本线性不可分样本在核孔间可分

• 分类​

  

  高斯核（RBF、径向基函数）：产生将样本投射到无限维空间运算效果，使得原来不可分数据变得可分。使用最多

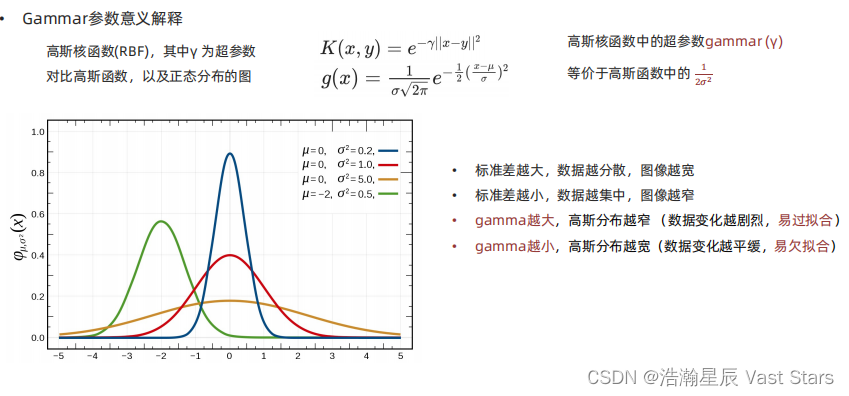
• 高斯核函数γ作用

  

• 高斯函数API

  • 导包： from sklearn.svm import SVC

  • 实例化：SVC（kernel='rbf' gamma=gamma）

  • gamama：值越大，高斯分布越窄（数据变化越剧烈，易过拟合），反之，值越小，高斯分布越宽（数据变化越平缓），易欠拟合，rbf是高斯核

  • gamama参数意义