二叉搜索树BST ——（C++）

        本篇将会讲解有关二叉树的搜索原理，以及关于二叉搜索树的建立，以及二叉树搜索树的插入、删除和查找等基本操作。最后我们还会对二叉搜索树进行功能扩展，介绍有关搜索二叉树的 K 模型和 KV 模型。目录如下：

目录

1. 搜索二叉树

二叉搜索树概念

二叉树类框架

搜索二叉树的插入

搜索二叉树的查找

搜索二叉树的遍历

搜索二叉树的删除

搜索二叉树所有代码

测试

 2. 搜索二叉树的扩展

中英文查找测试代码

统计单词次数测试代码

1. 搜索二叉树

二叉搜索树概念

        二叉搜索树又称二叉排序树，也可以是一棵空树。对于搜索二叉树具有以下性质：

                1. 若左子树不为空，则左子树上所有结点的值都小于根节点的值；

                2. 若右子树不为空，则右子树上所有结点的值都大于根节点的值；

                3. 它的左右子树也分别是二叉搜索树。

        关于二叉搜索树为什么叫做二叉排序树，这是因为左子树小于根节点，右子树大于根节点（二叉搜索树中的元素默认不会重复），当我们使用中序遍历（左 中 右）的时候，遍历刚好出来是有序的。

二叉树类框架

        建立一颗二叉树，首先需要一个结点的类，然后我们需要使用一个根节点将其维护起来。如下：

template <class K>
struct BSTreeNode {BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};template <class K>
class BSTree {
public:typedef BSTreeNode<K> Node;private:Node* _root;
};

搜索二叉树的插入

        关于搜索二叉树的插入，我们只需要找到合适的位置将其插入即可。也就是当我们需要插入的元素大于当前元素的时候，我们就继续往右子树放，反之放在左值树，直到到空结点的时候，我们还需要记录当前搜索结点的父亲结点，便于之后将其连接起来，我们就可以插入元素了。

        注：默认搜索二叉树不含有重复元素，所以当插入重复元素的时候，插入失败。

bool insert(const K& key) {if (_root == nullptr) {_root = new Node(key);return true;}// 左子树小于根节点，右子树大于根节点Node* cur = _root;Node* parent = nullptr;while (cur) {if (key > cur->_key) {parent = cur;cur = cur->_right;}else if (key < cur->_key) {parent = cur;cur = cur->_left;}else {return false;}}cur = new Node(key);if (key < parent->_key)parent->_left = cur;elseparent->_right = cur;return true;
}

搜索二叉树的查找

        查找遵循搜索二叉树的性质，当需要查找的数小于当前结点的时候，我们往左子树查找，当需要查找的数大于当前结点的时候，我们往右边查找。若直到空结点都还没有查找到，那么就查找失败了。如下：

bool find(const K& key) {Node* cur = _root;while (cur) {if (key > cur->_key) {cur = cur->_right;}else if (key < cur->_key) {cur = cur->_left;}else {return true;}}return false;
}

搜索二叉树的遍历

        搜索二叉树的遍历我们采用中序遍历，因为遍历出来的结果就是有序的。我们使用递归遍历。但是我们需要注意的一点是，我们在遍历的时候，需要访问到根节点，但是若我们在类外想要遍历的时候，我们并不能传一个被 private 保护的根节点的，所以我们需要进行如下的封装，就不需要进行传参了。如下：

template <class K>
class BSTree {
public:typedef BSTreeNode<K> Node;// 中序遍历void InOrder() {_InOrder(_root);cout << endl;}private:void _InOrder(Node* root) {// 左中右if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}
private:Node* _root;
};

搜索二叉树的删除

        关于搜索二叉树结点的删除，会存在很多的情况，如：删除的位置是叶子结点，删除的位置左子树为空，删除的位置右子树为空，删除的位置左右子树都不为空，删除的位置为根节点，且左子树或右子树为空。

        所以搜索二叉树的删除实现较为复杂，首先需要找到该位置，若直到空结点都还未找到，则二叉树中并无该元素，删除失败，返回 false；

        若删除的位置是叶子结点，删除的位置左子树为空，删除的位置右子树为空：我们先讨论删除位置的左子树为空，那么删除位置右节点可能不为空，所以删除该位置之后需要将删除位置的父亲结点的指针（可能是左，也可能是右）指向删除结点的右子树。删除位置的右子树为空，那么删除位置左节点可能不为空，所以删除该位置之后需要将删除位置的父亲结点的指针（可能是左，也可能是右）指向删除结点的左子树。当我们实现以上的两种情况的时候，我们发现删除位置是叶子结点的问题也迎刃而解了。

        删除的位置左右子树都不为空：当我们删除位置的左子树和右子树都不为空的时候，我们就需要讨论一个问题，删除该位置之后，左右子树该如何进行连接？答案是找到左子树的最大节点（最右结点）或者找到右子树的最小结点（最左结点）将其替换即可，替换之后在将其删除即可，但是其中还有一个不可忽视的问题，当我们替换之后删除的位置并不是叶子结点的时候，又该如何进行连接呢？以替换删除的结点为右子树的最小结点为例子，我们需要将删除结点的父亲结点指向（可能是左指针也可能是右指针，需要判断）删除结点的右子树。

        删除的位置为根节点，且左子树或右子树为空：当需要删除的结点为根结点且一端的子树为空的时候，我们只需要将根节点往另一个相反的结点移位即可。如下：

        将会对每种情况在代码中注释：

bool erase(const K& key) {// 先寻找key，找到删除，没找到直接返回falseNode* cur = _root;Node* parent = nullptr;while (cur) {if (key > cur->_key) {parent = cur;cur = cur->_right;}else if (key < cur->_key) {parent = cur;cur = cur->_left;}else {break;}}if (cur == nullptr) return false;// 需要删除位置的左子树或右子树为空if (cur->_left == nullptr) {// 删除位置为根节点if (parent == nullptr) {parent = cur;_root = cur->_right;delete parent;return true;}else {if (parent->_right == cur)parent->_right = cur->_right;elseparent->_left = cur->_right;delete cur;}}else if (cur->_right == nullptr) {if (parent == nullptr) {parent = cur;_root = cur->_left;delete parent;return true;}else {if (parent->_right == cur)parent->_right = cur->_left;elseparent->_left = cur->_left;delete cur;}}else {// 删除左右子树都有元素的结点// 找到右边最小的Node* rightMin = cur->_right;Node* rightMinParent = cur;while (rightMin->_left) {rightMinParent = rightMin;rightMin = rightMin->_left;}// 现在的rightMin为右子树最小结点元素std::swap(cur->_key, rightMin->_key);// 若要删除的结点如父亲结点的左结点，链接左边if (rightMinParent->_right == rightMin)rightMinParent->_right = rightMin->_right;elserightMinParent->_left = rightMin->_right;delete rightMin;}return true;
}

搜索二叉树所有代码

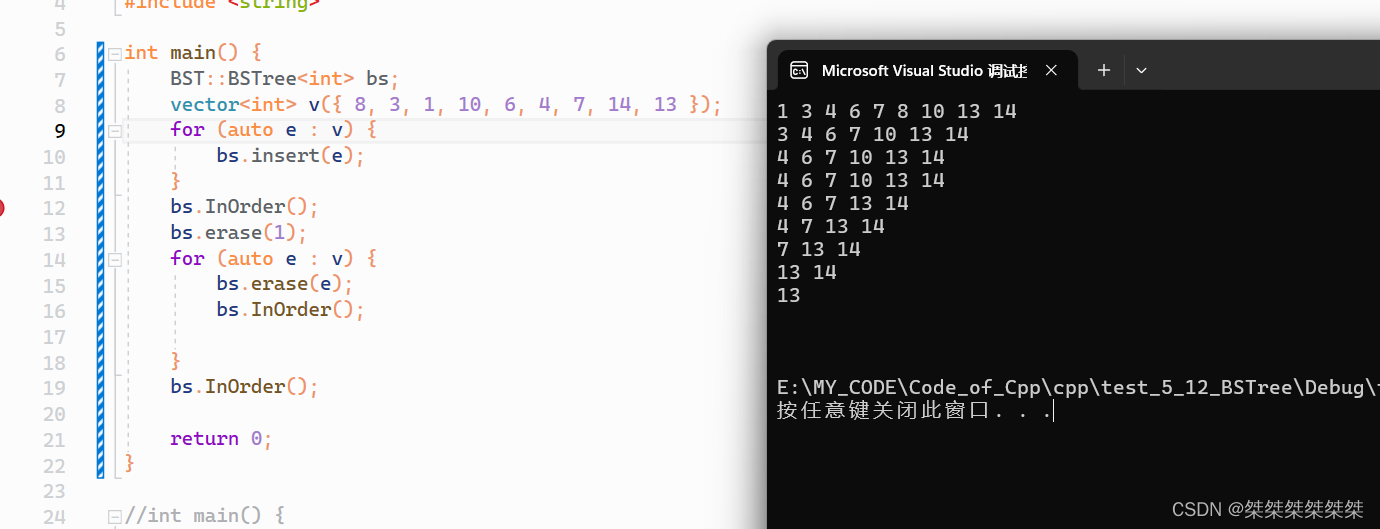
template <class K>
struct BSTreeNode {BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};template <class K>
class BSTree {
public:typedef BSTreeNode<K> Node;// 构造函数BSTree() : _root(nullptr) {}// 插入、删除、查找、遍历函数bool insert(const K& key) {if (_root == nullptr) {_root = new Node(key);return true;}// 左子树小于根节点，右子树大于根节点Node* cur = _root;Node* parent = nullptr;while (cur) {if (key > cur->_key) {parent = cur;cur = cur->_right;}else if (key < cur->_key) {parent = cur;cur = cur->_left;}else {return false;}}cur = new Node(key);if (key < parent->_key)parent->_left = cur;elseparent->_right = cur;return true;}bool find(const K& key) {Node* cur = _root;while (cur) {if (key > cur->_key) {cur = cur->_right;}else if (key < cur->_key) {cur = cur->_left;}else {return true;}}return false;}bool erase(const K& key) {// 先寻找key，找到删除，没找到直接返回falseNode* cur = _root;Node* parent = nullptr;while (cur) {if (key > cur->_key) {parent = cur;cur = cur->_right;}else if (key < cur->_key) {parent = cur;cur = cur->_left;}else {break;}}if (cur == nullptr) return false;// 现在的 cur 是我们需要删除的结点// 若该结点为根节点if (cur->_left == nullptr) {if (parent == nullptr) {parent = cur;_root = cur->_right;delete parent;return true;}else {if (parent->_right == cur)parent->_right = cur->_right;elseparent->_left = cur->_right;delete cur;}}else if (cur->_right == nullptr) {if (parent == nullptr) {parent = cur;_root = cur->_left;delete parent;return true;}else {if (parent->_right == cur)parent->_right = cur->_left;elseparent->_left = cur->_left;delete cur;}}else {// 删除左右子树都有元素的结点// 找到右边最小的Node* rightMin = cur->_right;Node* rightMinParent = cur;while (rightMin->_left) {rightMinParent = rightMin;rightMin = rightMin->_left;}// 现在的rightMin为右子树最小结点元素std::swap(cur->_key, rightMin->_key);// 若要删除的结点如父亲结点的左结点，链接左边if (rightMinParent->_right == rightMin)rightMinParent->_right = rightMin->_right;elserightMinParent->_left = rightMin->_right;delete rightMin;}return true;}void InOrder() {_InOrder(_root);cout << endl;}private:void _InOrder(Node* root) {// 左中右if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}
private:Node* _root;
};int main() {BSTree<int> bs;vector<int> v({ 8, 3, 1, 10, 6, 4, 7, 14, 13 });for (auto e : v) {bs.insert(e);}bs.InOrder();bs.erase(1);for (auto e : v) {bs.erase(e);bs.InOrder();}bs.InOrder();return 0;
}
测试

 2. 搜索二叉树的扩展

        关于搜索二叉树一共存在两种模型，一种为 K 模型，另一种为 KV 模型，如下：

        K 模型：K 模型即只有 key 作为关键码，结构中只需要存储 key 即可，关键码即为需要搜索到的值。（也就是上文中实现的搜索二叉树）

        KV 模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。
        关于 KV 模型，比如：英汉词典就是英文与中文的对应关系、统计单词次数，统计成功后，给定单词就可快速找到其出现的次数。

        关于 KV 模型的实现和 K 模型大同小异，如下：

template <class K, class V>
struct BSTreeNode {BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr),_right(nullptr),_key(key),_value(value){}
};template <class K, class V>
class BSTree {
public:typedef BSTreeNode<K, V> Node;// 构造函数BSTree() : _root(nullptr) {}// 插入、删除、查找、遍历函数bool insert(const K& key, const V& value) {if (_root == nullptr) {_root = new Node(key, value);return true;}// 左子树小于根节点，右子树大于根节点Node* cur = _root;Node* parent = nullptr;while (cur) {if (key > cur->_key) {parent = cur;cur = cur->_right;}else if (key < cur->_key) {parent = cur;cur = cur->_left;}else {return false;}}cur = new Node(key, value);if (key < parent->_key)parent->_left = cur;elseparent->_right = cur;return true;}Node* find(const K& key) {Node* cur = _root;while (cur) {if (key > cur->_key) {cur = cur->_right;}else if (key < cur->_key) {cur = cur->_left;}else {return cur;}}return nullptr;}bool erase(const K& key) {// 先寻找key，找到删除，没找到直接返回falseNode* cur = _root;Node* parent = nullptr;while (cur) {if (key > cur->_key) {parent = cur;cur = cur->_right;}else if (key < cur->_key) {parent = cur;cur = cur->_left;}else {break;}}if (cur == nullptr) return false;// 现在的 cur 是我们需要删除的结点// 若该结点为根节点if (cur->_left == nullptr) {if (parent == nullptr) {parent = cur;_root = cur->_right;delete parent;return true;}else {if (parent->_right == cur)parent->_right = cur->_right;elseparent->_left = cur->_right;delete cur;}}else if (cur->_right == nullptr) {if (parent == nullptr) {parent = cur;_root = cur->_left;delete parent;return true;}else {if (parent->_right == cur)parent->_right = cur->_left;elseparent->_left = cur->_left;delete cur;}}else {// 删除左右子树都有元素的结点// 找到右边最小的Node* rightMin = cur->_right;Node* rightMinParent = cur;while (rightMin->_left) {rightMinParent = rightMin;rightMin = rightMin->_left;}// 现在的rightMin为右子树最小结点元素std::swap(cur->_key, rightMin->_key);// 若要删除的结点如父亲结点的左结点，链接左边if(rightMinParent->_right == rightMin)rightMinParent->_right = rightMin->_right;elserightMinParent->_left = rightMin->_right;delete rightMin;}return true;}void InOrder() {_InOrder(_root);cout << endl;}private:void _InOrder(Node* root) {// 左中右if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << " " << root->_value << endl;_InOrder(root->_right);}
private:Node* _root;
};
中英文查找测试代码
int main() {BSTree<string, string> bs;string s1 = "insert";string v1 = "插入";string s2 = "right";string v2 = "右边";string s3 = "left";string v3 = "左边";bs.insert(s1, v1);bs.insert(s2, v2);bs.insert(s3, v3);string s;while (cin >> s) {if (bs.find(s))cout << bs.find(s)->_value << endl;elsecout << "没有该单词的含义" << endl;}return 0;
}
统计单词次数测试代码
int main() {string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
"苹果", "香蕉", "苹果", "香蕉" };BSTree<string, int> bs;for (auto& str : arr) {auto ret = bs.find(str);if (ret == nullptr)bs.insert(str, 1);elseret->_value++;}bs.InOrder();return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/842153.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

前端学习CSS-2

前端学习CSS-2

盒子模型 盒子模型相关属性 一些盒子模型的样式示例 传统网页布局方式 浮动 浮动的三大特性 脱标&#xff1a;脱离标准流一行显示&#xff0c;顶部对齐具备行内块元素特性 定位
阅读更多...
粤嵌—2024/5/17—N 皇后 ||（✔）

粤嵌—2024/5/17—N 皇后 ||（✔）

代码实现&#xff1a;
阅读更多...
Java整合EasyExcel实战——1

Java整合EasyExcel实战——1

参考&#xff1a;读Excel | Easy Excel快速使用easyexcel的来完成excel的读取https://easyexcel.opensource.alibaba.com/docs/current/quickstart/read 准备条件 依赖 <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifa…
阅读更多...
Android 动效整理

Android 动效整理

Android自定义SeekBar&#xff0c;滑动时弹出气泡指示器显示进度 安卓开发中非常炫的效果集合_android 开发 向右上角收起炫酷动态效果-CSDN博客 https://github.com/shenghuntianlang/Android-Views?tabreadme-ov-file#decentbanner 以前收藏了很多文章&#xff0c;但是过…
阅读更多...
【UE5.1 角色练习】08-传送技能

【UE5.1 角色练习】08-传送技能

前言 在上一篇&#xff08;【UE5.1 角色练习】07-AOE技能&#xff09;基础上继续实现人物通过鼠标点击然后传送技能的功能。 效果 步骤 1. 首先需要显示鼠标光标&#xff0c;我们可以在玩家控制器中勾选“显示鼠标光标” 2. 在项目设置中添加一个操作映射&#xff0c;设置按…
阅读更多...
Python爬虫入门实例：Python7个爬虫小案例（附源码）

Python爬虫入门实例：Python7个爬虫小案例（附源码）

引言 随着互联网的快速发展&#xff0c;数据成为了新时代的石油。Python作为一种高效、易学的编程语言&#xff0c;在数据采集领域有着广泛的应用。本文将详细讲解Python爬虫的原理、常用库以及实战案例&#xff0c;帮助读者掌握爬虫技能。 一、爬虫原理 爬虫&#xff0c;又…
阅读更多...
Vue3.0 里为什么要用 Proxy API替代 defineProperty API？

Vue3.0 里为什么要用 Proxy API替代 defineProperty API？

Vue3.0选择使用Proxy API替代defineProperty API的原因主要有以下几点&#xff1a; 性能提升&#xff1a; Proxy API允许拦截整个对象&#xff0c;而defineProperty API需要遍历对象的每个属性进行拦截。因此&#xff0c;Proxy API在捕获对象的访问和修改时更为高效。 更全面的…
阅读更多...
maptr(2):论文及代码解读

maptr(2):论文及代码解读

文章目录 1. 介绍2. 模型架构2.1 GT 数据制作2.2 模型架构2.3 GKT2.3.1 cross attn 的变化2.3.1 GKT2.4 decoder部分2.5 header2.5.1 reg_branch2.5.2 cls_branch3. Loss计算3.1 正负样本匹配3.2 loss计算<
阅读更多...
2024年上半年信息系统项目管理师下午真题及答案(第二批)

2024年上半年信息系统项目管理师下午真题及答案(第二批)

试题一 某项目计划工期为10个月&#xff0c;预算210万元&#xff0c;第7个月结束时&#xff0c;项目经理进行了绩效评估&#xff0c;发现实际完成了总计划进度的70%。项目的实际数据如表所示&#xff1a; 单击下面头像图片领取更多软考独家资料
阅读更多...
企业内部通讯软件—WorkPlus适配信创即时通讯软件

企业内部通讯软件—WorkPlus适配信创即时通讯软件

在现代企业中&#xff0c;良好的内部通讯是保持高效工作和顺利运营的关键。企业内部通讯软件的选择对于提升沟通效率、促进团队合作、保障数据安全和隐私保护至关重要。本文将介绍企业内部通讯软件的重要性探讨一些常用的软件&#xff0c;帮助企业做出明智的选择。 一、企业内…
阅读更多...
深度融合大语言模型与知识图谱：思通数科企业知识库智能问答系统的创新实践

深度融合大语言模型与知识图谱：思通数科企业知识库智能问答系统的创新实践

摘要 在知识经济时代&#xff0c;企业知识管理的重要性日益凸显。本文深入探讨了思通数科如何利用大语言模型和知识图谱技术&#xff0c;构建企业知识库智能问答系统&#xff0c;以促进知识的高效获取、共享、应用和创新&#xff0c;从而提升企业的知识管理水平和业务价值。 1…
阅读更多...
钕铁硼表面磷化处理

钕铁硼表面磷化处理

大家都知道烧结钕铁硼易氧化、易腐蚀&#xff0c;日久将造成磁性能的衰减甚至丧失&#xff0c;所以使用前必须进行严格的防腐处理。在之前的文章中已经向大家介绍过与烧结钕铁硼表面处理相关的知识和电镀的工艺流程&#xff0c;除了电镀之外&#xff0c;钕铁硼表面处理还可采用…
阅读更多...
Reids高频面试题汇总总结

Reids高频面试题汇总总结

一、Redis基础 Redis是什么？ Redis是一个开源的内存数据存储系统，它可以用作数据库、缓存和消息中间件。Redis支持多种数据结构，如字符串、哈希表、列表、集合、有序集合等，并提供了丰富的操作命令来操作这些数据结构。Redis的主要特点是什么？ 高性能：Redis将数据存储在内…
阅读更多...
大数据开发面试题【ClickHouse篇】

大数据开发面试题【ClickHouse篇】

170、clickhouse介绍以及架构 clickhouse一个分布式列式存储数据库&#xff0c;主要用于在线分析查询 171、列式存储和行式存储有什么区别&#xff1f; 行式存储&#xff1a; 1、数据是按行存储的 2、没有建立索引的查询消耗很大的IO 3、建立索引和视图花费一定的物理空间和…
阅读更多...
查看Mongo是否正在备份？

查看Mongo是否正在备份？

要查看MongoDB是否正在备份&#xff0c;可以通过以下几种方法&#xff1a; 查看MongoDB的进程列表&#xff1a; 使用命令ps -ef | grep mongo&#xff0c;这将列出所有正在运行的MongoDB进程。在输出的列表中&#xff0c;你可以查看是否有与备份相关的进程或任务正在运行。 查…
阅读更多...
rapidssl通配符证书低至600元一年

rapidssl通配符证书低至600元一年

RapidSSL是Geotrust旗下的子品牌&#xff0c;主要经营的是入门级的SSL数字证书。RapidSSL旗下的SSL证书产品不多&#xff0c;只有DV基础型单域名SSL证书和通配符SSL证书&#xff0c;不过这两款SSL证书满足了大多数网站的需求。今天就随SSL盾小编了解RapidSSL旗下的通配符SSL证书…
阅读更多...
C# 结构体（Struct）

C# 结构体（Struct）

1. 结构体的基本概念 在C#中，结构体是一种值类型，用于封装一组相关的数据。与类（Class）不同，结构体的实例存储在栈上，而不是堆上，因此结构体的性能通常比类更高，特别是在需要频繁创建和销毁实例时。 2. 结构体的声明和使用 你可以使用struct关键字来声明一个结构体：…
阅读更多...
【补充1】字节对齐

【补充1】字节对齐

文章目录 1.字节对齐的基本概念2.字节对齐规则3.实践出真知&#xff08;加大难度&#xff09;4 位域 1.字节对齐的基本概念 &#xff08;1&#xff09;现代计算机中内存空间都是按照byte划分的&#xff0c; 从理论上讲似乎对任何类型的变量的访问可以从任何地址开始&#xff0…
阅读更多...
MybatisPlus中自定义sql

MybatisPlus中自定义sql

背景 在开发过程中&#xff0c;可能会出现除了where条件&#xff0c;其它sql比较复杂&#xff0c;这时候就需要用到自定义sql了。 问题 如&#xff1a;用户状态为正常的数据年龄加一&#xff08;所有用户年龄加一&#xff09; 数据库中sql&#xff1a; UPDATE USER SET…
阅读更多...
协变(List泛型作为方法参数时的父类子类问题)

协变(List泛型作为方法参数时的父类子类问题)

有段时间没搞.net的项目了&#xff08;没办法&#xff0c;谁让国内JAVA流行是事实&#xff09;。最近又回归.net&#xff08;哪里需要哪里搬~&#xff09;。 接收到需求后&#xff0c;一顿输出&#xff0c;结果…咦?编译失败??? 错误信息&#xff1a; CS1503:参数1:无法…
阅读更多...
最新文章

Copyright @ 2022~2023