最近想学一下Mamba模型,奈何看了很多视频还是感觉一知半解,因此做一篇笔记,顺便介绍一下Mamba结构作为CV backbone和时间序列预测领域的应用。
论文1. Mamba: Linear-Time Sequence Modeling with Selective State Spaces
0. Abstract
现有的基础模型都是以Transformer结构作为核心组建的。然而,Transformer中的注意力是二次方的复杂度,为了降低这个复杂度,一些线性注意力、门控卷积(gated convolution)和循环网络,以及状态空间模型(structured state space models,SSM)被提出,然而它们在一些重要的模态,例如语言中的性能并没有达到和Transformer中attention相媲美的程度。作者认为,这些方法的缺陷是它们无法进行基于内容的推理(content-based reasoning),因此Mamba做了一些改进。主要在于以下几点:
- 将SSM中的参数作为可学习的,也就是关于输入的一个函数,可以解决SSM在离散模态中的弱点,即可以有选择地沿序列长度维度传播或忘记信息。(可能是达到了LSTM记忆和遗忘的效果)
- 以上的这种改进无法再利用传统SSM中卷积形式的并行训练,但是作者提出了一个硬件级的并行算法来缓解这一问题。
- 作者将上述的改进成为Selective SSM,将其集成到一个简化的端到端的网络结构中,没有了繁杂的注意力机制和MLP blocks,成为Mamba。Mamba在语言、语音和基因序列相关的任务上表现都非常好。
具体的技术细节见下文。
1. Introduction and background
看完摘要不禁要问,作者说的现有方法的弱点:“无法进行基于内容的推理”,到底是什么含义呢?看看引言中是怎么讲的吧!
现有的基础模型都是以Transformer及其核心组件(self/cross attention)为基础的,但是这种注意力机制无法看到窗口之外(序列之外)的内容,并且在复杂度上和窗口长度成二次方关系。大量的注意力机制相关的变体虽然降低了复杂度,但是效果没跟上,并且在跨域的表现上都不好。
近期,结构化的状态空间模型在序列建模上引起了广泛的关注,它以经典的状态空间模型为启发,可以视作是RNN与CNN的结合。这一类模型既可以按照RNN的方式计算,也可以按照卷积的方式计算,并且具有和序列长度相关的近似线性复杂度,在非常多的任务中得到了应用。
上面这段话是什么意思呢?
考虑经典的线性时不变系统,输入为 x ( t ) x(t) x(t), 系统状态为 h ( t ) h(t) h(t), 输出为 y ( t ) y(t) y(t), 系统方程可以表示为:
h ˙ ( t ) = A h ( t ) + B x ( t ) y ( t ) = C h ( t ) + D x ( t ) \dot{h}(t)=Ah(t)+Bx(t) \\ y(t) = Ch(t) + Dx(t) h˙(t)=Ah(t)+Bx(t)y(t)=Ch(t)+Dx(t)
对于程序来说,我们当然希望程序处理离散而非连续的数据. 在SSM中,采用了零阶保持(zero-order holding)这样的操作来进行离散化的, 下面进行以下推导.
我们的最终目标是离散化成 h k + 1 = f ( h k ) h_{k + 1} = f(h_{k}) hk+1=f(hk)的形式. 我们先观察第一个式子, 重写为:
h ˙ ( t ) − A h ( t ) = B x ( t ) \dot{h}(t) - Ah(t)=Bx(t) h˙(t)−Ah(t)=Bx(t)
观察这个方程的形式, 考虑函数 F ( t ) = e − A t h ( t ) F(t)=e^{-At}h(t) F(t)=e−Ath(t), 则 F ˙ ( t ) = − A e − A t h ( t ) + e − A t h ˙ ( t ) \dot{F}(t)=-Ae^{-At}h(t)+e^{-At}\dot{h}(t) F˙(t)=−Ae−Ath(t)+e−Ath˙(t), 我们对上式两边同乘 e − A t e^{-At} e−At:
e − A t h ˙ ( t ) − A e − A t h ( t ) = e − A t B x ( t ) → F ˙ ( t ) = e − A t B x ( t ) e^{-At}\dot{h}(t) - Ae^{-At}h(t)=e^{-At}Bx(t) \\ \rightarrow \dot{F}(t)=e^{-At}Bx(t) e−Ath˙(t)−Ae−Ath(t)=e−AtBx(t)→F˙(t)=e−AtBx(t)
根据Roll定理: F ( t ) = F ( λ ) + ∫ λ t F ˙ ( τ ) d τ , ∀ λ F(t)=F(\lambda) + \int_{\lambda}^t\dot{F}(\tau) d \tau, \forall \lambda F(t)=F(λ)+∫λtF˙(τ)dτ,∀λ. 不妨令 λ = 0 \lambda = 0 λ=0, 有
F ( t ) = e − A t h ( t ) = F ( 0 ) + ∫ 0 t e − A τ B x ( τ ) d τ = h ( 0 ) + ∫ 0 t e − A τ B x ( τ ) d τ F(t)=e^{-At}h(t) = F(0)+ \int_{0}^t e^{-A\tau}Bx(\tau) d \tau = h(0) + \int_{0}^t e^{-A\tau}Bx(\tau) d \tau F(t)=e−Ath(t)=F(0)+∫0te−AτBx(τ)dτ=h(0)+∫0te−AτBx(τ)dτ
即
h ( t ) = e A t h ( 0 ) + e A t ∫ 0 t e − A τ B x ( τ ) d τ h(t)=e^{At}h(0)+e^{At}\int_{0}^t e^{-A\tau}Bx(\tau) d \tau h(t)=eAth(0)+eAt∫0te−AτBx(τ)dτ
我们考虑离散化的形式, 令上式中 t = t k + 1 t=t_{k+1} t=tk+1:
h ( t k + 1 ) = e A t k + 1 h ( 0 ) + e A t k + 1 ∫ 0 t k + 1 e − A τ B x ( τ ) d τ h(t_{k+1}) = e^{At_{k+1}}h(0) + e^{At_{k+1}}\int_{0}^{t_{k+1}} e^{-A\tau}Bx(\tau) d \tau h(tk+1)=eAtk+1h(0)+eAtk+1∫0tk+1e−AτBx(τ)dτ
设 t k + 1 = t k + Δ t_{k+1} = t_{k} + \Delta tk+1=tk+Δ, 有
h ( t k + 1 ) = e A t k h ( 0 ) ⋅ e A Δ + e A t k ⋅ e Δ [ ∫ 0 t k + ∫ t k t k + 1 ] = e A Δ [ e A t k h ( 0 ) + e A t k ∫ 0 t k ] + e A t k + 1 ∫ t k t k + 1 = e A Δ h ( t k ) + e A t k + 1 ∫ t k t k + 1 e − A τ B x ( τ ) d τ h(t_{k+1}) = e^{At_{k}}h(0)\cdot e^{A\Delta} + e^{At_{k}} \cdot e^{\Delta} [\int_{0}^{t_k} + \int_{t_k}^{t_{k+1}}] \\ =e^{A\Delta}[e^{At_{k}}h(0) + e^{At_{k}}\int_{0}^{t_k}] + e^{At_{k+1}}\int_{t_k}^{t_{k+1}} \\ =e^{A\Delta} h(t_k)+ e^{At_{k+1}}\int_{t_k}^{t_{k+1}} e^{-A\tau}Bx(\tau) d \tau h(tk+1)=eAtkh(0)⋅eAΔ+eAtk⋅eΔ[∫0tk+∫tktk+1]=eAΔ[eAtkh(0)+eAtk∫0tk]+eAtk+1∫tktk+1=eAΔh(tk)+eAtk+1∫tktk+1e−AτBx(τ)dτ
其中为了方便, 积分内的内容被省略. 如果 Δ \Delta Δ足够小, 在积分项中可以用 x ( t k ) x(t_k) x(tk)来代替 x ( τ ) x(\tau) x(τ), 有
h ( t k + 1 ) = e A Δ h ( t k ) + e A t k + 1 ⋅ x ( t k ) ⋅ ∫ t k t k + 1 e − A τ B d τ → ( ∫ t k t k + 1 e − A τ d τ = − 1 A [ e − A t k + 1 − e − A t k ] ) = e A Δ h ( t k ) + e A t k + 1 ⋅ x ( t k ) [ − 1 A [ e − A t k + 1 − e − A t k ] ] B = e A Δ h ( t k ) − 1 A [ 1 − e A Δ ] B x ( t k ) h(t_{k+1}) = e^{A\Delta} h(t_k) + e^{At_{k+1}} \cdot x(t_k) \cdot \int_{t_k}^{t_{k+1}} e^{-A\tau}Bd \tau \\ \rightarrow (\int_{t_k}^{t_{k+1}} e^{-A\tau}d\tau = -\frac{1}{A}[e^{-At_{k+1}} -e^{-At_{k}}]) \\ =e^{A\Delta} h(t_k)+ e^{At_{k+1}} \cdot x(t_k) [-\frac{1}{A}[e^{-At_{k+1}} -e^{-At_{k}}]]B \\ =e^{A\Delta} h(t_k)-\frac{1}{A}[1-e^{A\Delta}]Bx(t_k) h(tk+1)=eAΔh(tk)+eAtk+1⋅x(tk)⋅∫tktk+1e−AτBdτ→(∫tktk+1e−Aτdτ=−A1[e−Atk+1−e−Atk])=eAΔh(tk)+eAtk+1⋅x(tk)[−A1[e−Atk+1−e−Atk]]B=eAΔh(tk)−A1[1−eAΔ]Bx(tk)
实际当中 A , B A, B A,B都是矩阵, 我们写成矩阵的形式:
h ( t k + 1 ) = e A Δ h ( t k ) + A − 1 [ e A Δ − I ] B x ( t k ) = e A Δ h ( t k ) + ( Δ A ) − 1 [ e A Δ − I ] Δ B x ( t k ) h(t_{k+1}) = e^{A\Delta} h(t_k) + A^{-1}[e^{A\Delta} -I]Bx(t_k) \\ = e^{A\Delta} h(t_k) +(\Delta A)^{-1} [e^{A\Delta} -I] \Delta Bx(t_k) h(tk+1)=eAΔh(tk)+A−1[eAΔ−I]Bx(tk)=eAΔh(tk)+(ΔA)−1[eAΔ−I]ΔBx(tk)
令 A ˉ = e A Δ , B ˉ = ( Δ A ) − 1 [ e A Δ − I ] Δ B \bar{A}=e^{A\Delta}, \bar{B} = (\Delta A)^{-1} [e^{A\Delta} -I] \Delta B Aˉ=eAΔ,Bˉ=(ΔA)−1[eAΔ−I]ΔB, 有
h ( t k + 1 ) = A ˉ h ( t k ) + B ˉ x ( t k ) h(t_{k+1})=\bar{A}h(t_k) + \bar{B}x(t_k) h(tk+1)=Aˉh(tk)+Bˉx(tk)
特别注意! 在SSM中, 与上式不同, 是期望通过0时刻得到0, 也即加了一个约束是 h ( 0 ) = B x ( 0 ) h(0)=Bx(0) h(0)=Bx(0), 因此采用的是如下的形式:
h ( t k + 1 ) = A ˉ h ( t k ) + B ˉ x ( t k + 1 ) h(t_{k+1})=\bar{A}h(t_k) + \bar{B}x(t_{k+1}) h(tk+1)=Aˉh(tk)+Bˉx(tk+1)
实际上在我看来, 区别不大, 因为积分近似的时候用 x ( t k ) x(t_k) x(tk)或者 x ( t k + 1 ) x(t_{k+1}) x(tk+1)均可
以上原论文公式1a, 1b, 2a
对于输出, 如果认为输出只与状态有关, 可以直接离散化为
y ( t k + 1 ) = C h ( t k + 1 ) y(t_{k+1})=Ch(t_{k+1}) y(tk+1)=Ch(tk+1)
以上论文2b 式
为什么说SSM融合了RNN与CNN的优点? 这是由于系统方程上述的形式允许输出 y ( t ) y(t) y(t)具有了递归和卷积的双重属性.
例如, 考察
y 2 = C h 2 = C ( A ˉ h 1 + B ˉ x 2 ) = C ( A ˉ ( A ˉ h 0 + B ˉ x 1 ) + B ˉ x 2 ) ( h 0 = B ˉ x 0 ) = C ( A ˉ ( A ˉ B ˉ x 0 + B ˉ x 1 ) ) + B ˉ x 2 ) y_2=Ch_2=C(\bar{A} h_{1} + \bar{B} x_{2}) \\ =C(\bar{A} (\bar{A} h_{0} + \bar{B} x_{1}) + \bar{B} x_2) \\ (h_0=\bar{B}x_0) = C(\bar{A} (\bar{A} \bar{B}x_0 + \bar{B} x_{1})) + \bar{B} x_2) y2=Ch2=C(Aˉh1+Bˉx2)=C(Aˉ(Aˉh0+Bˉx1)+Bˉx2)(h0=Bˉx0)=C(Aˉ(AˉBˉx0+Bˉx1))+Bˉx2)
所以
y 2 = [ C A ˉ 2 B ˉ , C A ˉ B ˉ , C B ˉ ] [ x 0 , x 1 , x 2 ] T y_2=[C \bar{A}^2\bar{B}, C\bar{A}\bar{B}, C\bar{B}] [x_0, x_1, x_2]^T y2=[CAˉ2Bˉ,CAˉBˉ,CBˉ][x0,x1,x2]T
对于 y k y_k yk, 令 K = [ C A ˉ k B ˉ , C A ˉ k − 1 B ˉ , … ] , x = [ x 0 , x 1 , … ] K = [C \bar{A}^k \bar{B}, C \bar{A}^{k-1} \bar{B}, \dots], x = [x_0, x_1, \dots] K=[CAˉkBˉ,CAˉk−1Bˉ,…],x=[x0,x1,…], 则
y k = K ∗ x y_k=K * x yk=K∗x
以上论文 3a, 3b式
所以SSM在训练时, 采用上述的卷积形式, 推理时直接进行递推过程, 快速生成输出.
我们继续看引言。作者说,本文在多个维度上对以往的传统SSM模型进行了改进, 使得改进后的模型能够达到和Transformer相当的性能, 并且是近似线性时间复杂度, 主要的贡献是以下三点:
- 选择机制. 从上面的公式可以看出, 传统的SSM在计算卷积或者递归计算时, 是treat input equally的. 也就是作者说的, 没有对输入有一个选择的机制, 或者说依赖于输入的机制(input-dependent manner). (这可能说的就是摘要中说的“无法进行基于内容的推理”的意思). 为了解决这个问题, 作者参数化了SSM的参数(例如 B , C , Δ B, C, \Delta B,C,Δ等, 见后文), 这允许模型过滤掉不相关的信息并无限地记住相关信息.
- 硬件感知的算法. 如果把 B , C , Δ B, C, \Delta B,C,Δ等参数变成可学习的, 或者和输入有关的, 那么就不能再按照上述的卷积公式计算了, 增加了计算量. 为了解决这个问题, 作者用扫描替代了卷积, 也在GPU的IO次数上做了一些优化. 至于扫描是什么意思呢? 一起读下去吧!
- 结构拓展. 作者把上面的改进和MLP结合在了一起, 做成了一种block, 成为Mamba. 这种结构就能和Transformer一样, 可以整合与拼接.
2. Methodology
2.1 动机: 按照压缩的方式来思考如何"选择"
作者认为, 序列建模的根本任务就是把一个较大的输入状态(信息量等)压缩到一个较小的状态. 如果从这个角度看待现有模型的话, 注意力机制属于效果好, 但效率不高的, 这是因为它根本不压缩信息. 为什么呢? 因为在自回归的推理过程中, 需要KV cache来存储整个的内容信息. 对于回归模型, 其有(代表之前所有内容的)一个终极的状态, 这样在时间复杂度上低了, 但是性能也受制于这个最终状态"表示"内容的能力.
为了更好地说明上面的观点, 作者拿两个任务举例子:
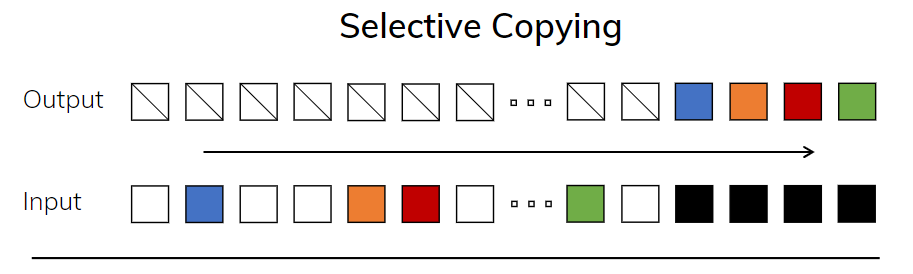
- 选择性复制任务. 相比于正常的复制任务, 选择性复制任务变换了token的顺序, 看看模型是否能copy出正确的顺序, 这考验了模型对内容的理解能力. 如下图所示:

这是传统的copy任务, 输入和输出保持了线性的关系, 可以通过LTI系统轻松得出, 例如一种延时: y = x ( t − Δ t ) y=x(t-\Delta t) y=x(t−Δt)这种的. 但下图是选择性的copy任务, 这用LTI系统就解决不了了.
2. Instruction Heads任务. 这个任务是说让LLM在适当的上下文时机生成输出, 比如下图的黑色框, 就代表合适的时机.
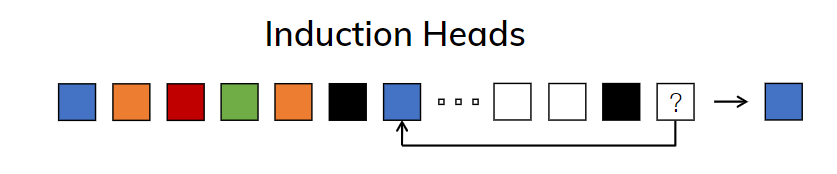
总之, 作者想说的就是两点:
- 在上面两个任务中, LTI系统做不到, 因此传统的SSM做不到.
- 效率&效果的平衡问题, 要想效果就得保存所有必要的的信息, 要想效率则要仔细思考如何尽量压缩状态. 与此相反, 作者的意思是, 我就去选择有用的输入, 没有用的要过滤掉, 来实现一种trade-off.
作者的做法就是, 从参数下手, 将 B , C , Δ B, C, \Delta B,C,Δ都变成可学习的, 或者说时变的, 就可以对输入进行选择了. 具体是怎么实现的呢?
拿 B B B来说, 如果输入的维度是 [ L , D ] [L, D] [L,D], 即序列长度为 L L L, 每个token的维数是 D D D, 系统状态维数为 N N N. 原本的LTI系统参数是时不变的, 因此 B B B的维度就是 [ D , N ] [D, N] [D,N]. 现在作者加一个维度, 序列长度, 因此参数就是时变的了. 下面的伪代码写的很清楚:

实现从输入到参数映射的方式就是MLP就可以了,
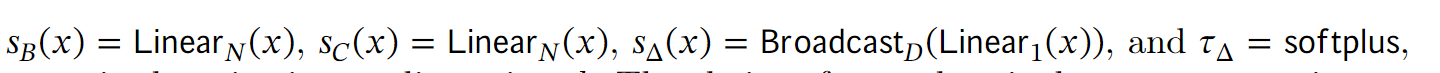
为什么 A ˉ \bar{A} Aˉ的维度是 [ B , L , D , N ] [B, L, D, N] [B,L,D,N] ? 待补充
3. Selective SSMs的高效实现
前面说过, 一旦这样成时变的, 就不能再像卷积那样一下子生成所有输出了. 作者在这里给出的主要改进是, 将离散化, 递归等过程放在GPU速度快的SRAM中, 而将最终的结果传回HBM中, 这样避免在低速的HBM中计算离散化之后的 A ˉ \bar{A} Aˉ, 因为其维度是 [ B , L , D , N ] [B, L, D, N] [B,L,D,N], 而 B , C B, C B,C等的维度都是 [ B , L , N ] [B, L, N] [B,L,N].
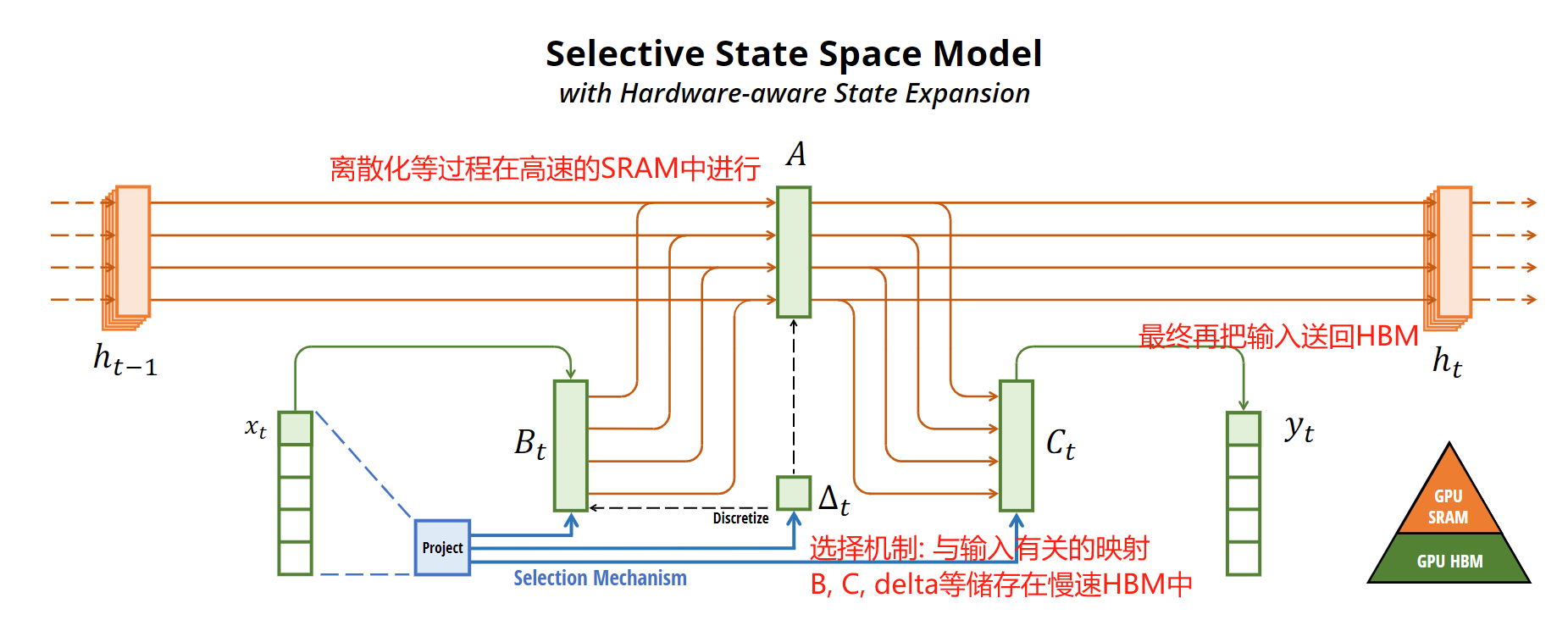
由于我对硬件不太懂, 这里有些地方我也不太明白. 我认为是从硬件上的策略优化以及类并行运算的扫描算法弥补了无法真正并行卷积运算的不足.
4. 简化的Selective SSM结构(Mamba)
作者想将前面提出的Selective SSM整合到神经网络中, 借鉴了过去H3网络和门控卷积的思想, 提出了Mamba Block:
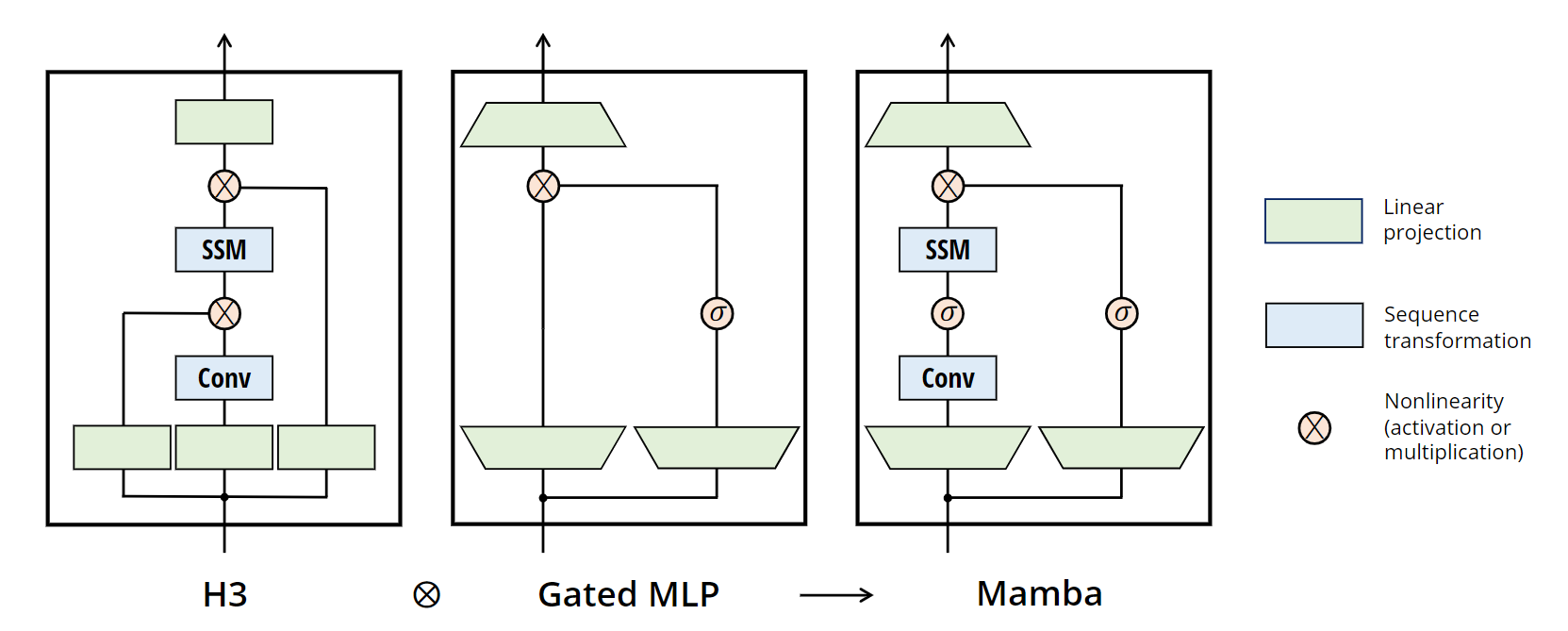
从图中可以看出, Mamba block首先对输入做了一个MLP映射, 作者说的是将 D D D通过一个可控制的拓展因子 E E E进行拓展. 在这个block中, 主要的计算量都来自于MLP. 在所有的实验室中, 作者为了模拟和多头注意力相当的计算量, 保持 E = 2 E=2 E=2, block的堆叠数目也是2.
其他的实验部分就先略过~ 下面说几个近期出现的应用
论文2. 视觉主干: VMamba: Visual State Space Model
这些就主要先记录一下核心思想.
对于ViT来说, 计算复杂度是patch数目的平方, 因为一个patch要和所有其他的patch产生联系. 然而, 借鉴Mamba的思想, 作者提出了横着, 竖着方向的扫描策略, 将这些patch转成sequence之后送入Mamba block进行学习:
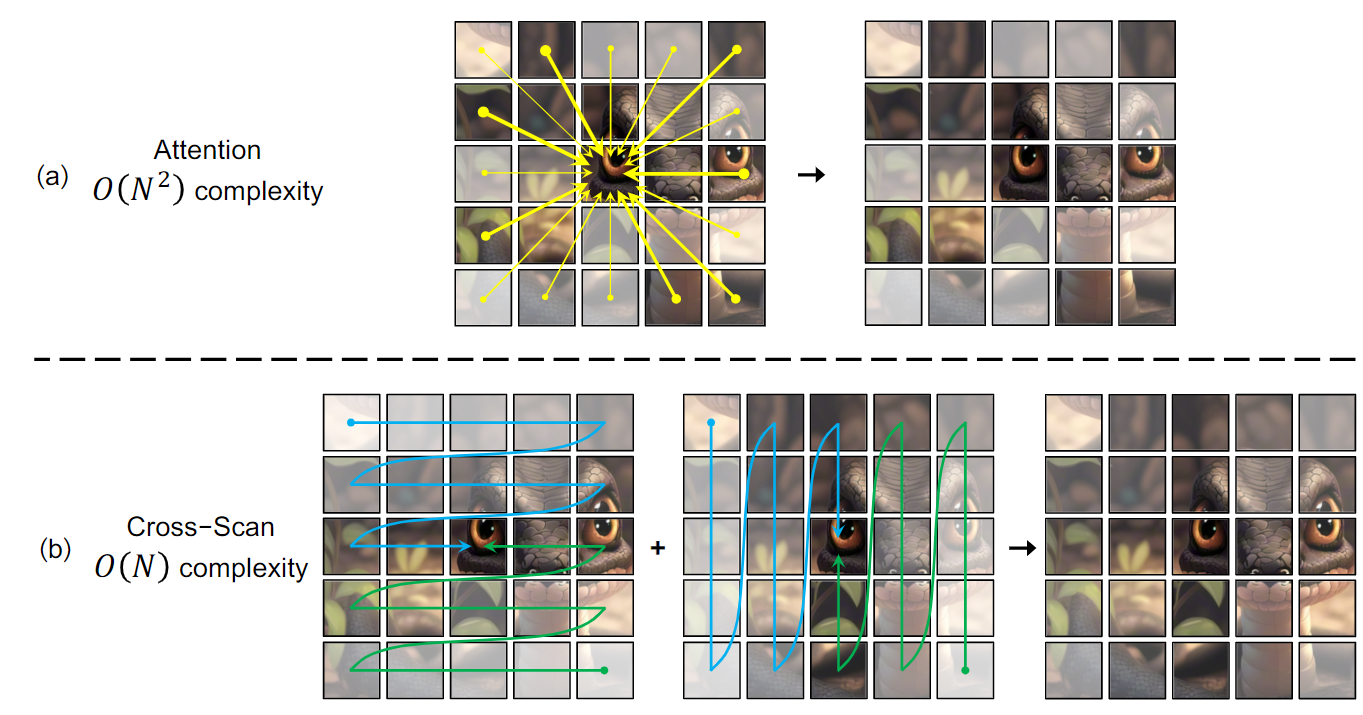
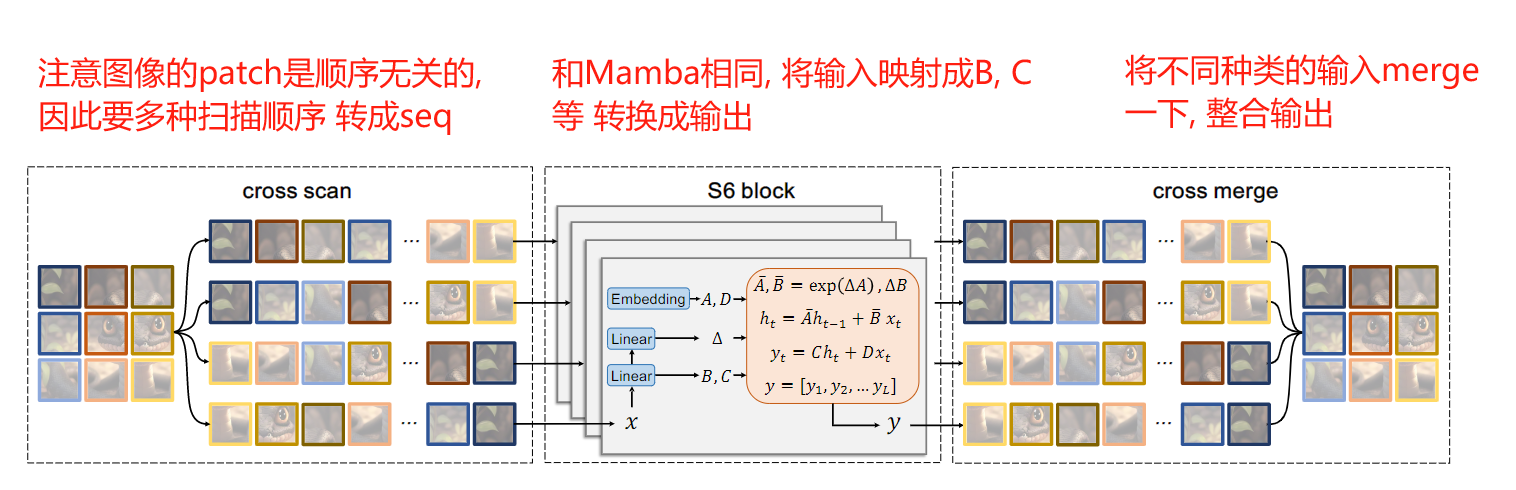
论文3. 视觉主干: Vision Mamba: Efficient Visual Representation Learning with Bidirectional State Space Model
借鉴ViT的思想, 不过它没有将输入patch的顺序打乱, 而是在Encoder的每个block中采用了双向的SSM计算, 也即用1D Conv对输入进行转换, 转换成一个正向和一个负向.
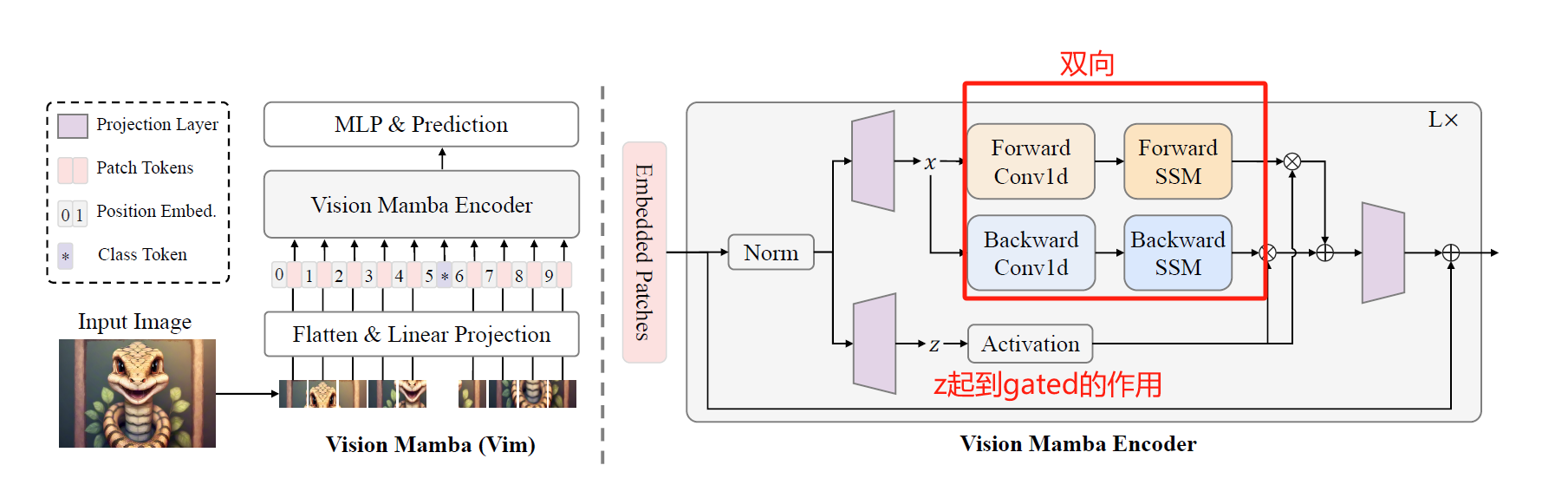
实际上, 把Mamba原本的图顺时针旋转90度, 加上一个反向分支, 就是Vision Mamba block了
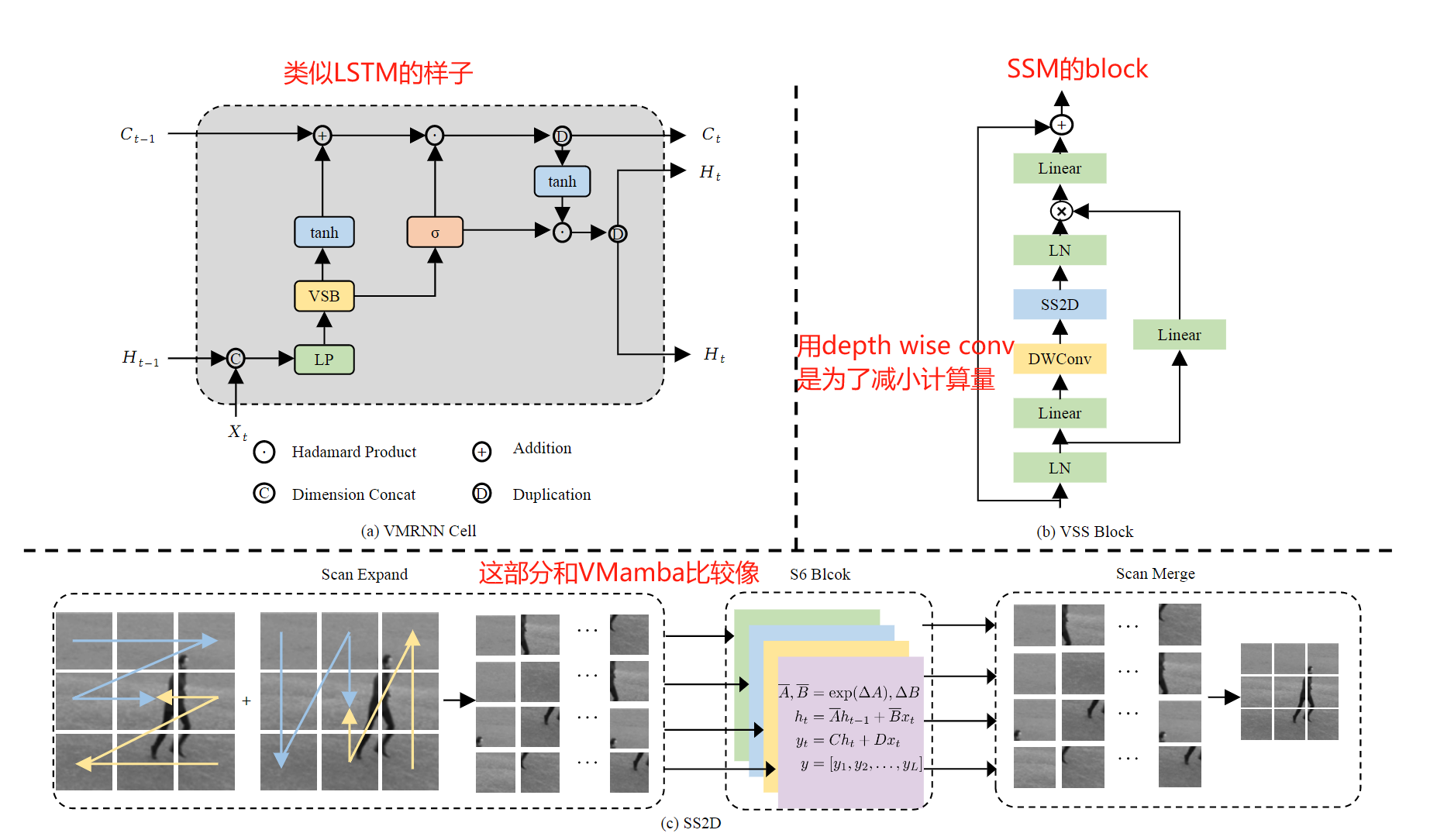
论文4. 时空预测: VMRNN: Integrating Vision Mamba and LSTM for Efficient and Accurate Spatiotemporal Forecasting
顾名思义, 为了进一步发挥Vision Mamba在时空数据上的效果, 将Vision Mamba和LSTM结合了起来~
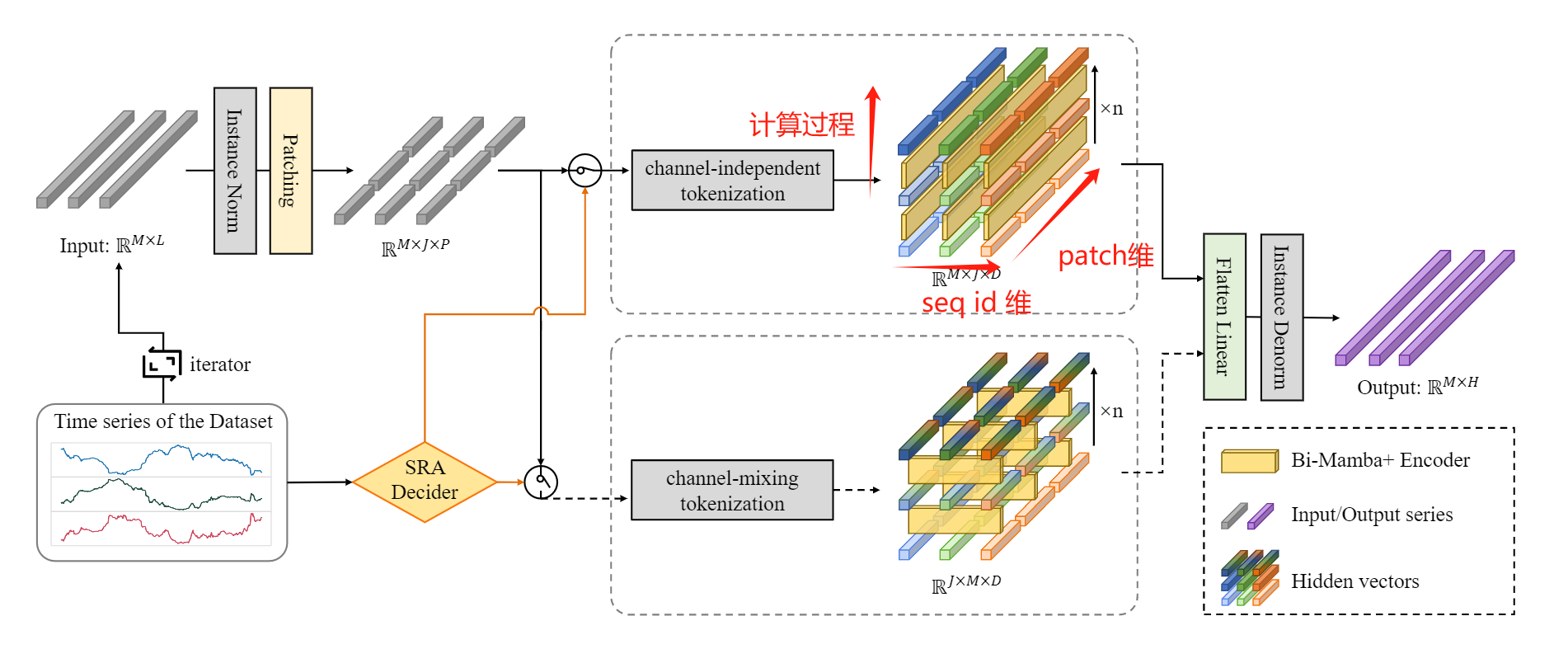
论文5. 时间序列预测: Bi-Mamba+: Bidirectional Mamba for Time Series Forecasting
序列问题, 当然适合时间序列预测的体质. 本文首先将时间序列打成patch, 然后在不同的维度(即, 首先对每个序列的patch维度, 搞一次Mamba块的seq2seq, 然后, 在序列维度, 搞一次seq2seq, 最后进行融合):
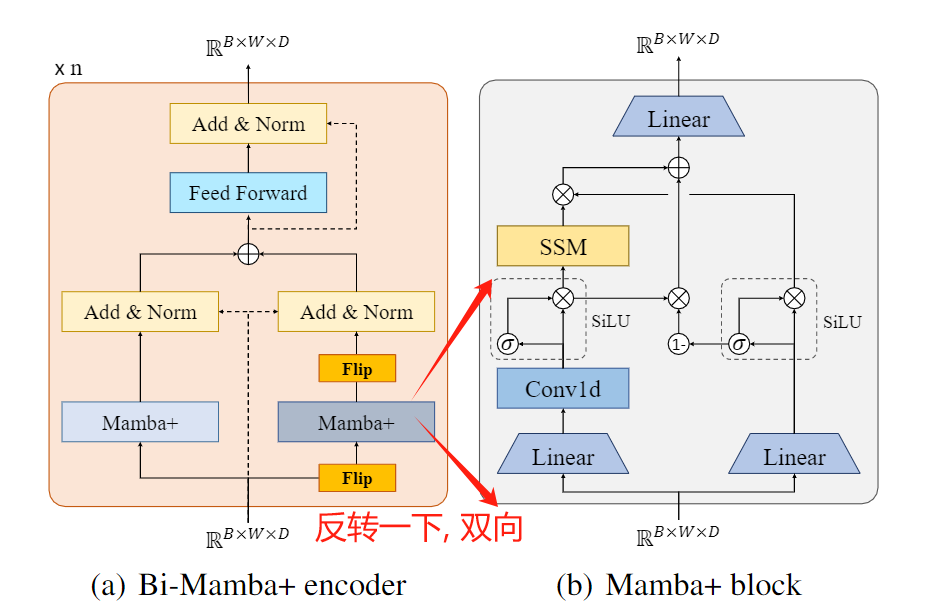
然后, 每个计算的block采用bi directional的机制
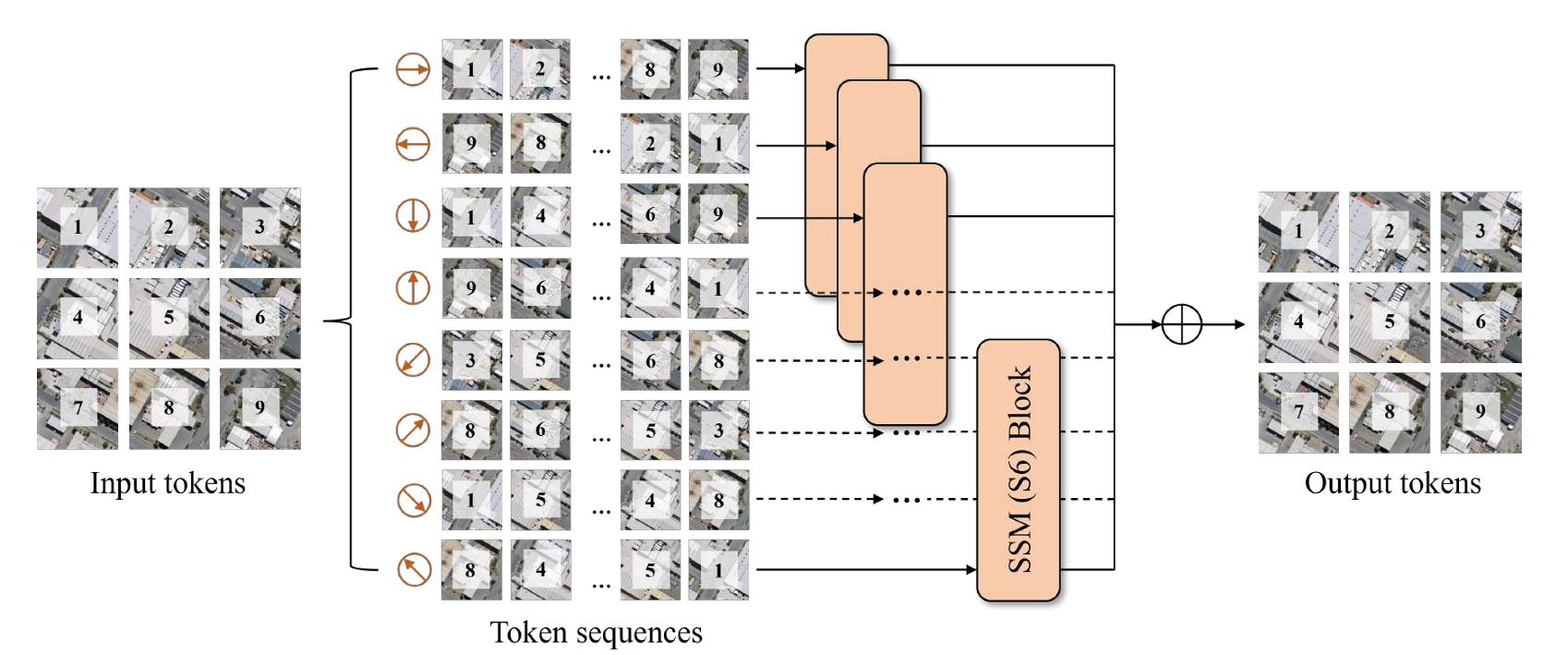
论文6. 遥感分割与变化检测: RS-Mamba for Large Remote Sensing Image Dense Prediction
这篇文章相比于前几个工作, 拓展了扫描算法的可能性, 左右上下对角线, 一共八种.
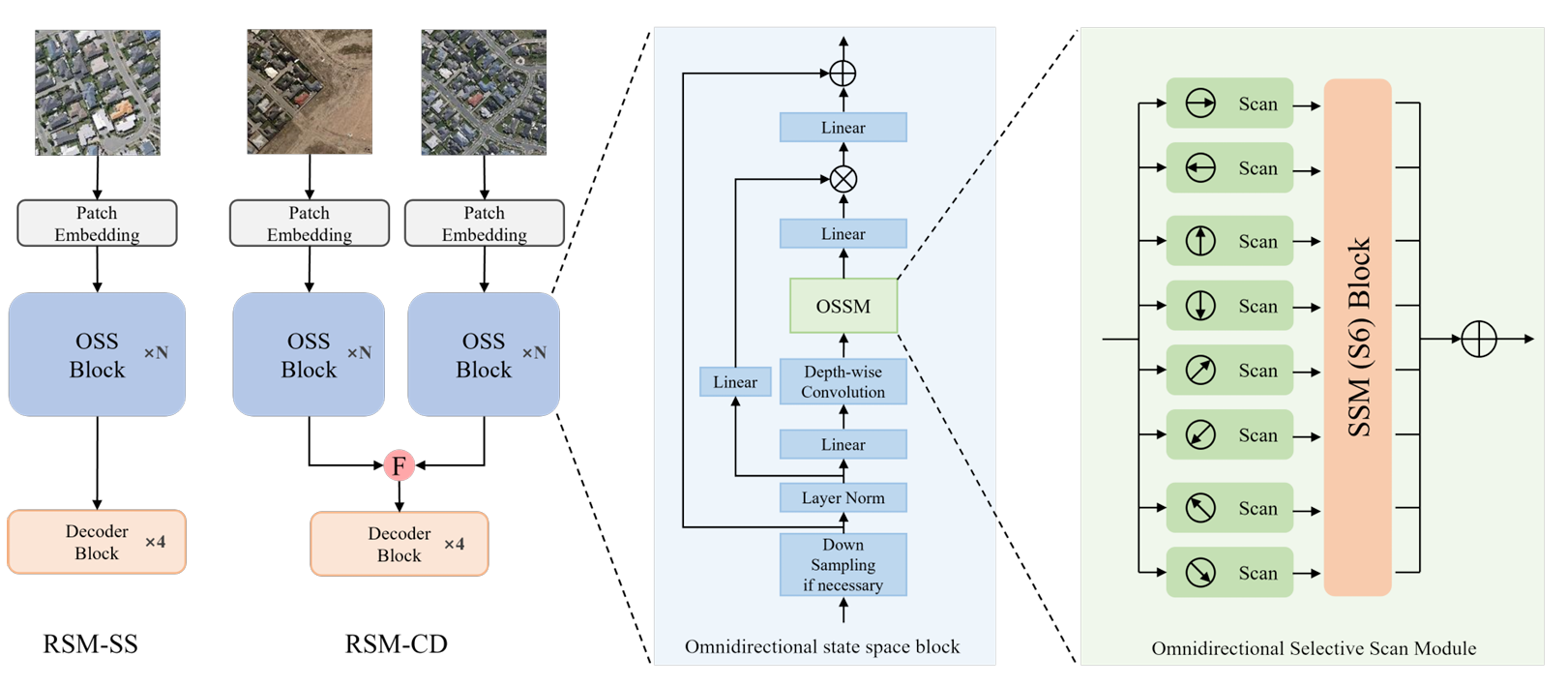
八种分别经过SSM block后, 按照原本的patch id回复并相加即可

)
)





![安全分析[2]之计算机系统安全分析](http://pic.xiahunao.cn/安全分析[2]之计算机系统安全分析)

)




)



