黑翅鸢是一种上半身蓝灰色,下半身白色的小型鸟类。它们的显著特征包括迁徙和捕食行为。它们以小型哺乳动物、爬行动物、鸟类和昆虫为食,具有很强的悬停能力,能够取得非凡的狩猎成功。受其狩猎技能和迁徙习惯的启发,该算法作者建立了基于黑翅鸢的算法模型。

基本原理:
(1)初始化:与其他大多数的此类算法一样,采用随机初始化,黑翅鸢的位置作为解。

pop是潜在解的个数,dim是给定问题维数的大小,BKij是第i个黑翅鸢的第j个维数。式中:i为介于1和pop之间的整数,BKlb和BKub分别为第i只黑翅风筝在第j维的下界和上界,rand为[ 0、1 ]之间随机选取的值。
(2)攻击行为
作为小型草原哺乳动物和昆虫的捕食者,黑翅鸢在飞行过程中根据风速调整翅膀和尾角,静静地悬停以观察猎物,然后迅速潜水和攻击。该策略包含针对全局探索和搜索的不同攻击行为。图a展示了一个黑翅鸢在空中盘旋、展翅并保持平衡的场景。


图a展示了一个黑翅鸢在空中盘旋、展翅并保持平衡的场景,且图a展示了黑翅鸢以极快的速度冲向猎物的场景。图b展示了黑翅鸢在空中盘旋时的攻击状态,且图b展示了黑翅鸢在空中盘旋时的状态。下面给出黑翅鸢攻击行为的数学模型:
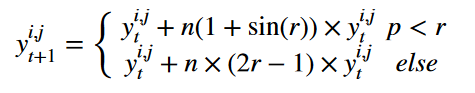

yi,jt和yi,jt + 1分别表示第i只黑翅鸢在第t步和第(t+1)步迭代中第j维的位置。r是一个取值范围为0到1的随机数,p是一个取值为0.9的常数。T是总的迭代次数,t是到目前为止已经完成的迭代次数。
这些都很好理解,但是原文并未给出n是什么东西的说明。
(3)迁移行为
鸟类迁徙是为了适应季节变化,许多鸟类在冬季从北方向南方迁徙,以获得更好的生存条件和资源。迁移通常由领导带领,他们的导航能力对团队的成功至关重要。
该算法提出了一个基于鸟群迁徙的假设:如果当前种群的适应度值小于随机种群的适应度值,领导者就会放弃领导,加入迁徙种群,说明不适合领导种群向前迁徙。

反之,如果当前种群的适应度值大于随机种群的适应度值,则引导种群直到到达目的地。这种策略可以动态地选择优秀的领导者,保证迁移的成功。上图为黑翅鸢迁徙过程中领鸟的变化情况。下面是关于迁移行为的一个数学模型:

![]()
Ljt代表了迄今为止第t次迭代的第j维黑翅鸢的领先得分者(当前最优解)。
yi,jt和yi,jt + 1分别表示第i只黑翅鸢在第t步和第(t+1)步迭代中第j维的位置。
C( 0、1 )代表柯西突变( Jiang , et al 2023)。其定义如下:
一维柯西分布是具有两个参数的连续概率分布。下面的方程说明了一维Cauchy分布的概率密度函数:

当δ = 1,μ = 0时,其概率密度函数将变为标准形式。下面是精确的公式:
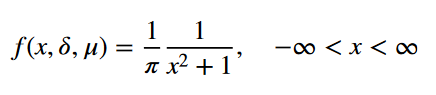
小说明一下(原文作者勿怪):
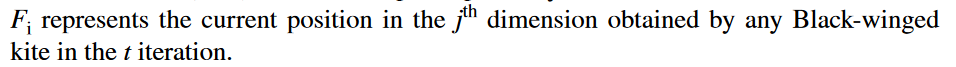
Fi表示任意黑翅鸢在第t次迭代中得到的第j维当前位置(注:这句话是上面这个文章图片原话的中文翻译,不过我觉得他这个描述有点问题。应该是:Fi是当前种群中任一个体的适应度值。因为他前面说了“如果当前种群的适应度值大于随机种群的适应度值,则引导种群直到到达目的地”。)。

Fri表示第t次迭代中任意一只黑翅鸢得到的第j维随机位置的适应度值(这也是原文的中文翻译,看不明白英文的可以直接看这个翻译)。
(这句话我觉得也是有问题的,我觉得做科研还是要严谨一点,毕竟写出来东西是要让人看的,新算法更是让人大量引用的。这个F根据他原文的描述很明显是适应度值,一个种群中有pop个个体,用i来表示,j是代表维度,y(i)是代表种群中的任一个体,那么再读读这句话“Fri表示第t次迭代中任意一只黑翅鸢得到的第j维随机位置的适应度值。”这句话明显有问题,首先适应度值是个体的适应度值,个体可以这么叫,个体中各个维度的那不叫适应度值(fitness value),叫值(value),个体中各个维度的值共同作用于目标函数得到适应度值。还有“Fri”这里都没有“j”这个字母,写这个的时候却带了这个字母的解释,这让人摸不着头脑。
具体拿这个刚运行的BKA来举例,

![]()
这个适应度值是3.3602e-103,那它上面那行的这个解的10个维度能叫适应度值吗?
总体上还好,不过这些都是小问题,瑕不掩瑜。告诉我们后来者写文章还是要严谨一些。
这是伪代码:

cec2005上测试:
F1:

F2:

F3:
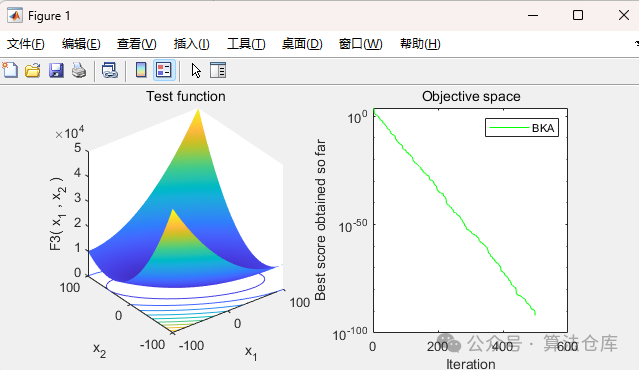
F4:
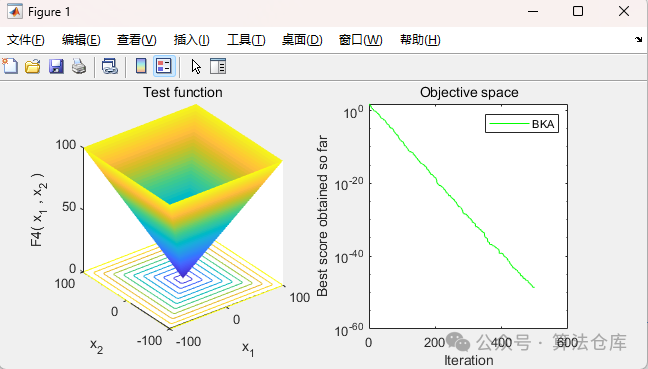
F5:
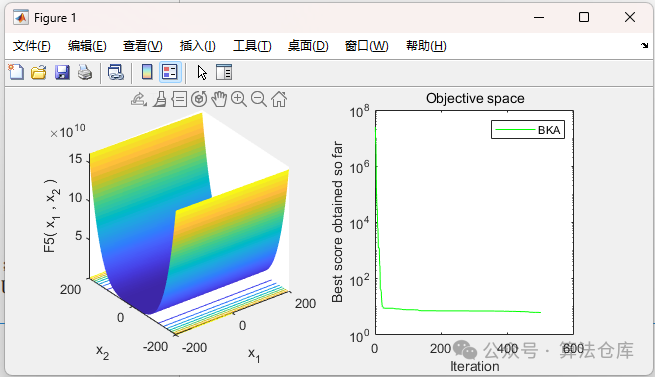
F6:

F7:

参考文献:
【1】Black‑winged kite algorithm: a nature‑inspired meta‑heuristic for solving benchmark functions and engineering problems(原文)
公众号:算法仓库,后台回复:BKA,即可免费获得此matlab版本代码,且包括原文。










)








