网址:
LLM Visualization
简介
欢迎来到 GPT 大型语言模型演练!在这里,我们将探索只有 85,000 个参数的 nano-gpt 模型。
它的目标很简单:取一个由六个字母组成的序列:
C B A B B C
并按字母顺序排列,即 "ABBBCC"。

我们称这些字母为一个标记,模型的不同标记集合构成了它的词汇表:
标记 A B C
索引 0 1 2
在这个表格中,每个标记都有一个数字,即标记索引。现在,我们可以将这一串数字输入模型:
2 1 0 1 1 2
在三维视图中,每个绿色单元格代表一个正在处理的数字,每个蓝色单元格代表一个权重。
-0.7
0.4
0.8
正在处理
-0.7
0.7
-0.1
权重
序列中的每个数字首先会被转化为 48 个元素向量(根据本特定模型选择的大小)。这就是所谓的嵌入。

然后,嵌入将穿过模型,经过一系列称为转换器的层,最后到达底层。
那么输出是什么呢?对序列中下一个标记的预测。因此,在第 6 个条目中,我们得到了下一个标记将是 "A"、"B "或 "C "的概率。
在这种情况下,模型非常确定会是 "A"。现在,我们可以将这一预测反馈到模型的顶层,并重复整个过程。
在深入了解算法的复杂性之前,我们先来回顾一下。
本指南侧重于推理而非训练,因此只是整个机器学习过程的一小部分。在我们的例子中,模型的权重已经预先训练好,我们使用推理过程来生成输出。这可以直接在浏览器中运行。
这里展示的模型是 GPT(生成式预训练转换器)系列的一部分,可以说是 "基于上下文的标记预测器"。OpenAI 在 2018 年引入了这一家族,其著名成员包括 GPT-2、GPT-3 和 GPT-3.5 Turbo,后者是广泛使用的 ChatGPT 的基础。它还可能与 GPT-4 有关,但具体细节仍不得而知。
本指南受到 minGPT GitHub 项目的启发,该项目是 Andrej Karpathy 在 PyTorch 中创建的最小 GPT 实现。他的 YouTube 神经网络系列:从零到英雄》系列和 minGPT 项目是创建本指南的宝贵资源。这里介绍的玩具模型基于 minGPT 项目中的一个模型。
好了,让我们开始吧!
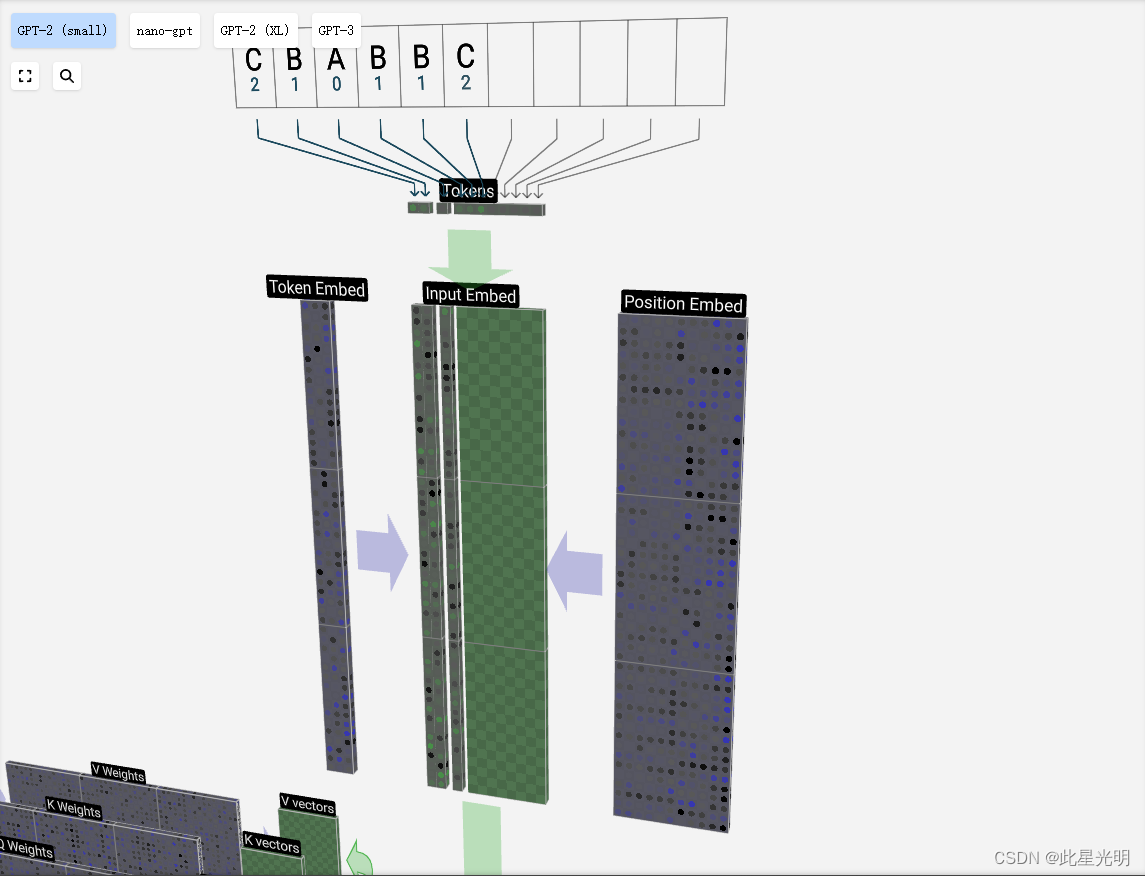
嵌入
我们之前看到过如何使用一个简单的查找表将标记映射为一串整数。这些整数,即标记索引,是我们在模型中第一次也是唯一一次看到的整数。从这里开始,我们将使用浮点数(十进制数)。
让我们来看看第 4 个标记(索引 3)是如何用于生成输入嵌入的第 4 列向量的。
我们使用标记索引(本例中为 B = 1)来选择左边标记嵌入矩阵的第 2 列。请注意,我们在这里使用的是基于 0 的索引,因此第一列的索引为 0。
这样就产生了一个大小为 C = 48 的列向量,我们将其描述为标记嵌入。
由于我们要查看的是位于第 4 个位置(t = 3)的标记 B,因此我们将取位置嵌入矩阵的第 4 列。
这也会产生一个大小为 C = 48 的列向量,我们将其描述为位置嵌入。
请注意,这些位置嵌入和标记嵌入都是在训练过程中学习的(用蓝色表示)。
现在我们有了这两个列向量,只需将它们相加,就能产生另一个大小为 C = 48 的列向量。
现在,我们对输入序列中的所有标记进行同样的处理,生成一组包含标记值及其位置的向量。
请将鼠标悬停在输入嵌入矩阵的各个单元格上,查看计算结果及其来源。
我们可以看到,对输入序列中的所有标记执行这一过程会产生一个大小为 T x C 的矩阵。T 代表时间,也就是说,你可以把序列中稍后的标记看作是时间上稍后的标记。C 代表通道,但也被称为 "特征"、"维度 "或 "嵌入大小"。这个长度 C 是模型的几个 "超参数 "之一,由设计者在模型大小和性能之间权衡选择。
这个矩阵,我们称之为输入嵌入,现在可以通过模型向下传递了。在本指南中,我们将非常熟悉由长度为 C 的 T 列组成的矩阵集合。
层规范
上一节的输入嵌入矩阵是我们第一个变换器模块的输入。
变换器模块的第一步是对该矩阵进行层归一化处理。这是对矩阵每列的值分别进行归一化的操作。
归一化是深度神经网络训练中的一个重要步骤,它有助于提高模型在训练过程中的稳定性。
我们可以分别看待每一列,所以现在先关注第 4 列(t = 3)。
我们的目标是使该列的平均值等于 0,标准差等于 1。为此,我们要找出该列的这两个量(平均值 (μ) 和标准差 (σ)),然后减去平均值,再除以标准差。
我们在这里使用的符号是 E[x] 表示平均值,Var[x] 表示方差(长度为 C 的列)。方差就是标准差的平方。ε项(ε = 1×10-5)的作用是防止除以零。
我们在聚合层中计算并存储这些值,因为我们要将它们应用于列中的所有值。
最后,在得到归一化值后,我们将列中的每个元素乘以一个学习权重 (γ),然后加上一个偏置 (β),最终得到我们的归一化值。
我们对输入嵌入矩阵的每一列进行这种归一化操作,得到的结果就是归一化后的输入嵌入,并可将其传入自注意层。
Self Attention
自我关注层或许是变换器和 GPT 的核心。在这一阶段,输入嵌入矩阵中的各列相互 "对话"。到目前为止,在所有其他阶段,各列都是独立存在的。
自我关注层由几个部分组成,我们现在将重点讨论其中的一个部分。
第一步是为归一化输入嵌入矩阵的每 T 列生成三个向量。这些向量就是 Q、K 和 V 向量:
Q:查询向量
K:键向量
V:值向量
要生成这些向量中的一个,我们要执行矩阵-向量乘法,并加上偏置。每个输出单元都是输入向量的线性组合。例如,对于 Q 向量来说,这是用 Q 权重矩阵的一行与输入矩阵的一列之间的点积来完成的。
我们会经常看到的点乘操作非常简单:我们将第一个向量中的每个元素与第二个向量中的相应元素配对,将配对的元素相乘,然后将结果相加。
这是一种确保每个输出元素都能受到输入向量中所有元素影响(这种影响由权重决定)的通用而简单的方法。因此,它经常出现在神经网络中。
我们对 Q、K、V 向量中的每个输出单元重复这一操作:
我们如何处理 Q(查询)、K(键)和 V(值)向量?命名给了我们一个提示:"key "和 "value "让人联想到软件中的字典,"key "映射到 "value"。那么 "查询 "就是我们用来查找值的。
软件类比
查找表:
table = { "key0":"value0", "key1":"value1", ...}
查询过程:
table["key1"] => "value1"
在自我关注的情况下,我们返回的不是单个条目,而是条目的加权组合。为了找到这种加权,我们在 Q 向量和 K 向量之间进行点乘。我们将加权归一化,最后用它与相应的 V 向量相乘,再将它们相加。
自我关注
查找表:
K:
V:
查询过程:
Q:
w0 =
.
w1 =
.
w2 =
.
[w0n, w1n, w2n] = .
正常化
([w0, w1, w2])
结果 = w0n *
+ w1n *
+ w2n *
举个更具体的例子,让我们看看第 6 列(t = 5),我们将从这一列开始查询:
我们查询的 {K, V} 项是过去的 6 列,Q 值是当前时间。
我们首先计算当前列(t = 5)的 Q 向量与之前各列的 K 向量之间的点积。然后将其存储在注意力矩阵的相应行(t = 5)中。
这些点积是衡量两个向量相似度的一种方法。如果两个向量非常相似,点积就会很大。如果两个向量差别很大,点积就会很小或为负。
只针对过去的密钥进行查询的想法使这种因果关系成为自我关注。也就是说,代币无法 "预见未来"。
另一个要素是,在求出点积后,我们要除以 sqrt(A),其中 A 是 Q/K/V 向量的长度。这种缩放是为了防止大值在下一步的归一化(软最大值)中占主导地位。
我们将跳过软最大操作(稍后描述),只需说明每一行的归一化总和为 1 即可。
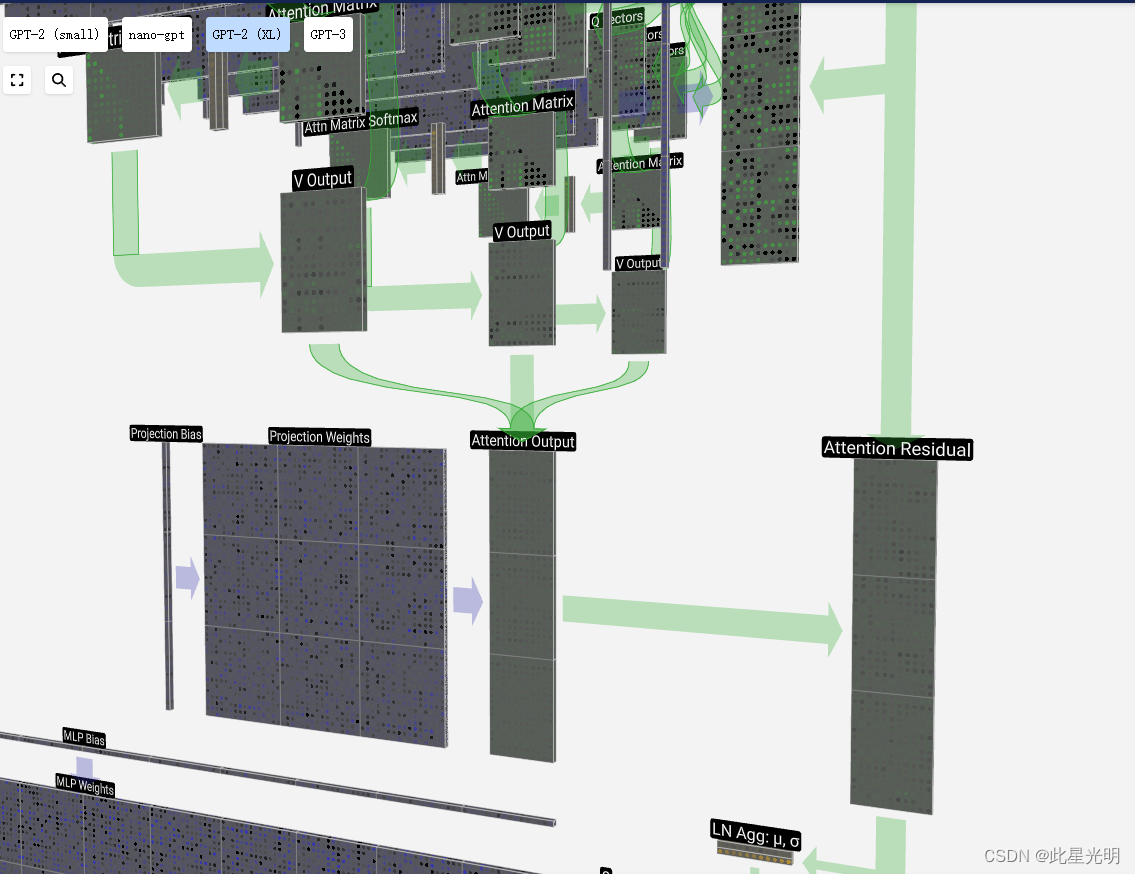
最后,我们就可以得到我们这一列(t = 5)的输出向量了。我们查看归一化自我关注矩阵的 (t = 5) 行,并对每个元素乘以其他列的相应 V 向量。
然后,我们就可以将这些相加得出输出向量。因此,输出向量将以高分列的 V 向量为主。
现在我们知道了这个过程,让我们对所有列进行运行。
这就是自我关注层头部的流程。自我关注的主要目标是,每一列都希望从其他列中找到相关信息并提取其值,并通过将其查询向量与其他列的键进行比较来实现这一目标。但有一个附加限制,即它只能查找过去的信息。
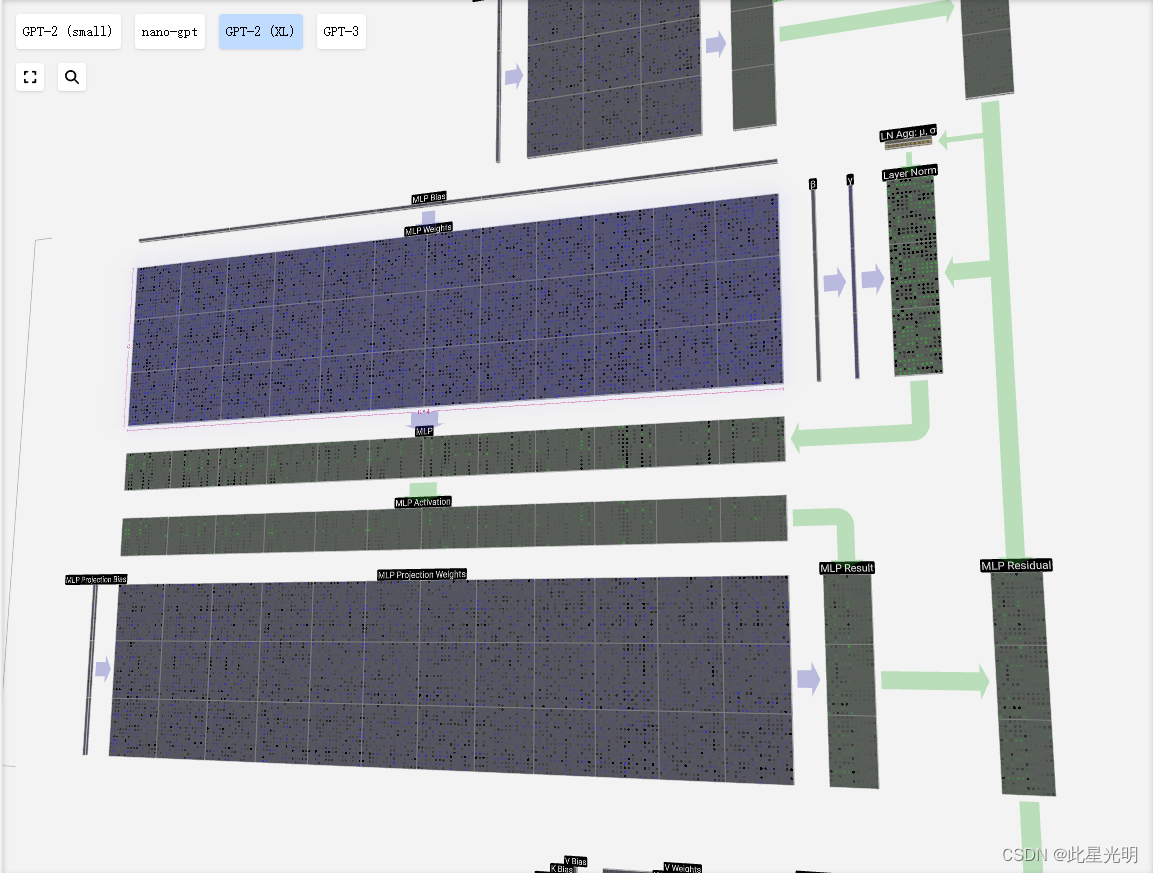
MLP
在自我注意之后,变压器模块的下半部分是 MLP(多层感知器)。虽然有点拗口,但在这里它是一个有两层的简单神经网络。
与自我注意一样,在向量进入 MLP 之前,我们也要进行层归一化处理。
在 MLP 中,我们将每个 C = 48 长度的列向量(独立)放入其中:
1.1. 添加偏置的线性变换,转换为长度为 4 * C 的向量。
2.一个 GELU 激活函数(按元素计算)
3.带偏置的线性变换,返回长度为 C 的矢量
让我们追踪其中一个向量:
我们首先执行带偏置的矩阵-向量乘法,将向量扩展为长度为 4 * C 的矩阵。这纯粹是为了可视化的目的)。
接下来,我们对向量的每个元素应用 GELU 激活函数。这是任何神经网络的关键部分,我们要在模型中引入一些非线性。使用的特定函数 GELU 看起来很像 ReLU 函数(计算公式为 max(0,x)),但它有一条平滑的曲线,而不是一个尖角。
-1
1
2
3
-3
-2
-1
1
2
3
然后,我们用另一个带偏置的矩阵-向量乘法将向量投影回长度 C。
与自我关注 + 投影部分一样,我们将 MLP 的结果按元素顺序添加到输入中。
现在,我们可以对输入中的所有列重复这一过程。
MLP 就这样完成了。现在我们有了转换器模块的输出,可以将其传递给下一个模块了。
Transformer
这是一个完整的转换模块!
这些转换构成了任何 GPT 模型的主体,并且会重复多次,一个转换的输出会馈入下一个变压器块,继续剩余通路。
与深度学习中常见的情况一样,我们很难说清楚这些层中的每一层都在做什么,但我们有一些大致的想法:较早的层往往侧重于学习较低层次的特征和模式,而较晚的层则学习识别和理解较高层次的抽象概念和关系。在自然语言处理中,低层可能学习语法、句法和简单的词汇关联,而高层可能捕捉更复杂的语义关系、话语结构和上下文相关的含义。
Softmax
如上一节所述,softmax 操作是自我关注的一部分,它也将出现在模型的最后。
它的目的是将一个向量的值归一化,使其总和为 1.0。然而,这并不像除以总和那么简单。相反,每个输入值都要先进行指数化处理。
a = exp(x_1)
这样做的效果是使所有值都为正。有了指数化值的向量后,我们就可以用每个值除以所有值的总和。这将确保所有数值之和为 1.0。由于所有指数化值都是正值,我们知道得出的值将介于 0.0 和 1.0 之间,这就提供了原始值的概率分布。
这就是 softmax 的原理:简单地将数值指数化,然后除以总和。
不过,还有一个小麻烦。如果输入值很大,那么指数化后的值也会很大。我们最终会用一个很大的数除以一个很大的数,这可能会导致浮点运算出现问题。
softmax 运算的一个有用特性是,如果我们在所有输入值上添加一个常数,结果将是相同的。因此,我们可以找到输入向量中的最大值,然后将其从所有值中减去。这样就能确保最大值为 0.0,从而使 softmax 在数值上保持稳定。
让我们结合自我注意层来看看 softmax 操作。每个 softmax 运算的输入向量都是自我注意矩阵的一行(但只到对角线)。
与层归一化一样,我们有一个中间步骤来存储一些聚合值,以保持流程的高效性。
对于每一行,我们都会存储该行的最大值以及移位值和指数值之和。然后,为了生成相应的输出行,我们可以执行一小套操作:减去最大值、指数化和除以总和。
为什么叫 "softmax"?这种操作的 "硬 "版本称为 argmax,它只是找出最大值,将其设为 1.0,并将所有其他值设为 0.0。相比之下,softmax 操作则是其 "柔和 "版本。由于 softmax 涉及指数运算,最大值会被强调并推向 1.0,同时仍保持所有输入值的概率分布。这样就能获得更细致的表示,不仅能捕捉到最有可能的选项,还能捕捉到其他选项的相对可能性。
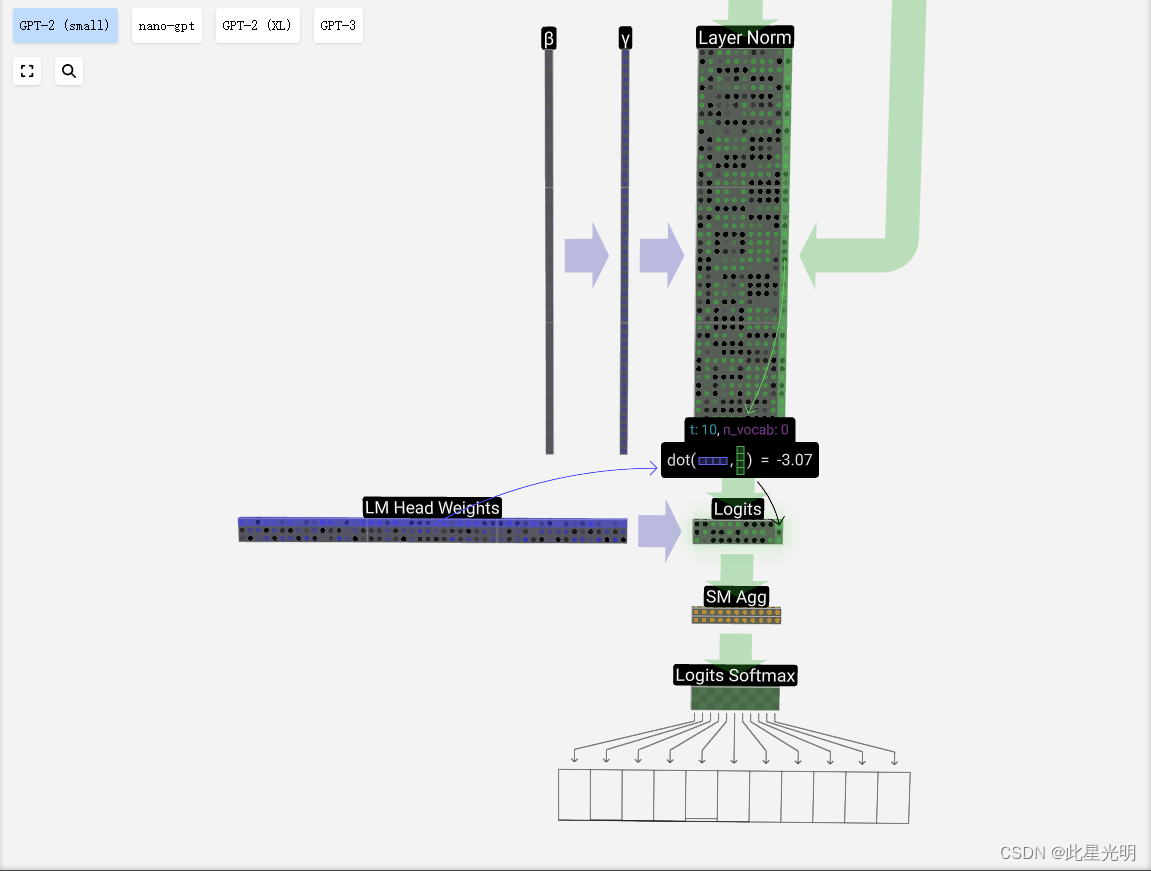
结果
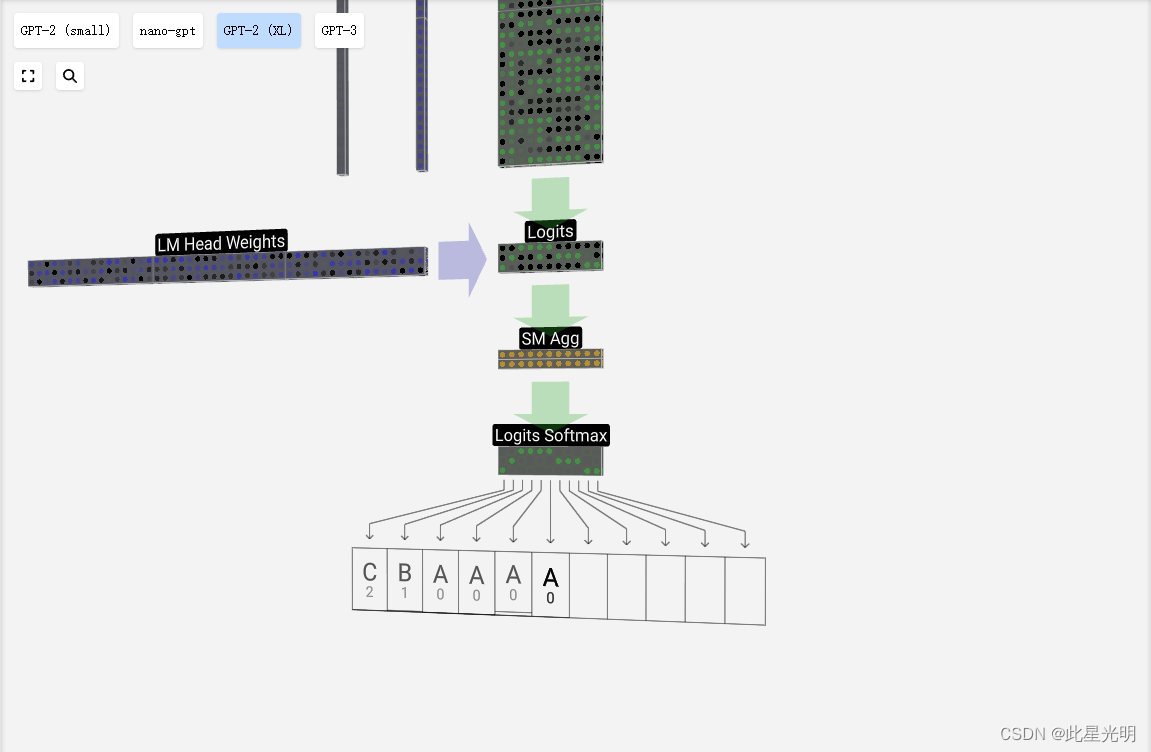
最后,我们来到模型的末端。最后一个变换器模块的输出经过层归一化处理,然后我们使用线性变换(矩阵乘法),这次没有偏差。
最后的变换将我们的每个列向量从长度 C 变为长度 nvocab。因此,这实际上是为我们每一列词汇中的每个单词生成一个分数。这些分数有一个特殊的名字:logits。
logits "这个名字来源于 "log-odds",即每个标记的几率的对数。之所以使用 "对数",是因为我们接下来应用的 softmax 会进行指数运算,将其转换为 "几率 "或概率。
为了将这些分数转换为漂亮的概率,我们将它们通过软最大运算。现在,对于每一列,我们都有了模型分配给词汇表中每个词的概率。
在这个特定的模型中,它已经有效地学习了如何对三个字母进行排序这一问题的所有答案,因此概率在很大程度上倾向于正确答案。
当我们对模型进行时间步进时,我们会使用上一列的概率来决定下一个要添加到序列中的标记。例如,如果我们已经向模型提供了 6 个标记,我们就会使用第 6 列的输出概率。
这一列的输出是一系列概率,我们实际上必须从中挑选一个作为序列中的下一个。我们通过 "从分布中采样 "来实现这一点。也就是说,我们随机选择一个标记,并根据其概率进行加权。例如,概率为 0.9 的令牌将在 90% 的情况下被选中。
不过,这里还有其他选择,比如总是选择概率最高的代币。
我们还可以使用温度参数来控制分布的 "平滑度"。温度越高,分布越均匀;温度越低,分布越集中在概率最高的标记上。
在应用 softmax 之前,我们先用温度除以 logits(线性变换的输出)。由于 softmax 中的指数化会对较大的数字产生较大影响,因此将所有数字拉近会减少这种影响。


)
)
)















