0. 前言

按照国际惯例，首先声明：本文只是我自己学习的理解，虽然参考了他人的宝贵见解及成果，但是内容可能存在不准确的地方。如果发现文中错误，希望批评指正，共同进步。

nn.ConvTranspose2d 模块是用于实现二维转置卷积（又称为反卷积）的核心组件。本文将详细介绍 ConvTranspose2d 的概念、工作原理、参数设置以及实际应用。

本文的说明参考了PyTorch的官方文档

1. 转置卷积概述

转置卷积（Transposed Convolution），有时也被称为“反卷积”（尽管严格来说它并不是真正意义上的卷积的逆运算），是一种特殊的卷积操作，常用于从较低分辨率的特征图上采样到较高分辨率的空间维度。

在诸如深度卷积生成对抗网络（DCGAN）和条件生成对抗网络（CGANs）等任务中，转置卷积被广泛用于将网络内部的紧凑特征（较小的特征）表示恢复为与原始输入尺寸相匹配或接近的（较大的特征）输出。

2. nn.ConvTranspose2d 模块详解

nn.ConvTranspose2d 是 PyTorch 中 torch.nn 模块的一部分，专门用于定义和实例化二维转置卷积层。其构造函数接受一系列参数来配置卷积行为：

2.1 主要参数

1. in_channels (int) - 输入特征图的通道数，即前一层的输出通道数。

2. out_channels (int) - 输出特征图的通道数，即本层产生的新特征通道数。

3. kernel_size (int 或 tuple) - 卷积核大小，通常是一个整数（当使用方形卷积核时）或包含两个整数的元组（分别对应卷积核的高度和宽度）。

4. stride (int 或 tuple, default=1) - 卷积步长，决定了卷积核在输入特征图上滑动的距离。与 kernel_size 类似，它可以是单个整数（对所有维度相同）或一个包含两个整数的元组。

5. padding (int 或 tuple, default=0) - 填充量，用于控制输出尺寸和保持边界信息。

6. output_padding (int 或 tuple, default=0) - 用于调整输出尺寸的额外填充量，仅应用于转置卷积。它在卷积计算后增加到输出边缘的额外像素数量。

7. groups (int, default=1) - 分组卷积参数，当大于1时，输入和输出通道将被分成若干组，每组内的卷积相互独立。

8. bias (bool, default=True) - 表示是否为该层添加可学习的偏置项。

9. dilation (int 或 tuple, default=1) - 卷积核元素之间的间距（膨胀率），控制卷积核中非零元素之间的距离。

10. padding_mode (str , default=zeros) - 填充数据方式，zeros为全部填充0

11. device (str , default=cpu) - 处理数据的设备

12. dtype (str, default=None ) - 数据类型

2.2 属性与方法

• .weight (Tensor) - 存储转置卷积核的权重，形状为 (out_channels, in_channels, kernel_size[0], kernel_size[1])，是可学习的模型参数。

• .bias (Tensor) - 若 bias=True，则包含与每个输出通道关联的偏置项，形状为 (out_channels)，也是可学习的参数。

• .forward(input) - 接受输入张量 input，执行转置卷积运算并返回输出特征图。

3. 计算过程（重点）

输入输出图像一般为4维或3维，即[B, C, H, W]或[C, H, W]，其中：

• B：Batch_size，每批的样本数
• C：channel，通道数
• H, W：图像的高和宽

以图像高度H为例（宽度W同理），转置卷积的输出尺寸可以通过以下公式计算：

$$H_{out}=(H_{in}-1)\times \text{stride}-2\times \text{padding}+\text{dilation}\times (\text{kernel-size}-1)+\text{output-padding}+1$$

这个公式看起来比较复杂，下面我们通过实例来理解转置卷积的计算过程。

3.1 基本过程

输入原图size为[1, 2, 2]，卷积核也size也为[1, 2, 2]，其余参数如下：

in_channels=1, out_channels=1, kernel_size=2, stride=1, padding=0, output_padding=0,dilation=1,bias=False

计算过程：

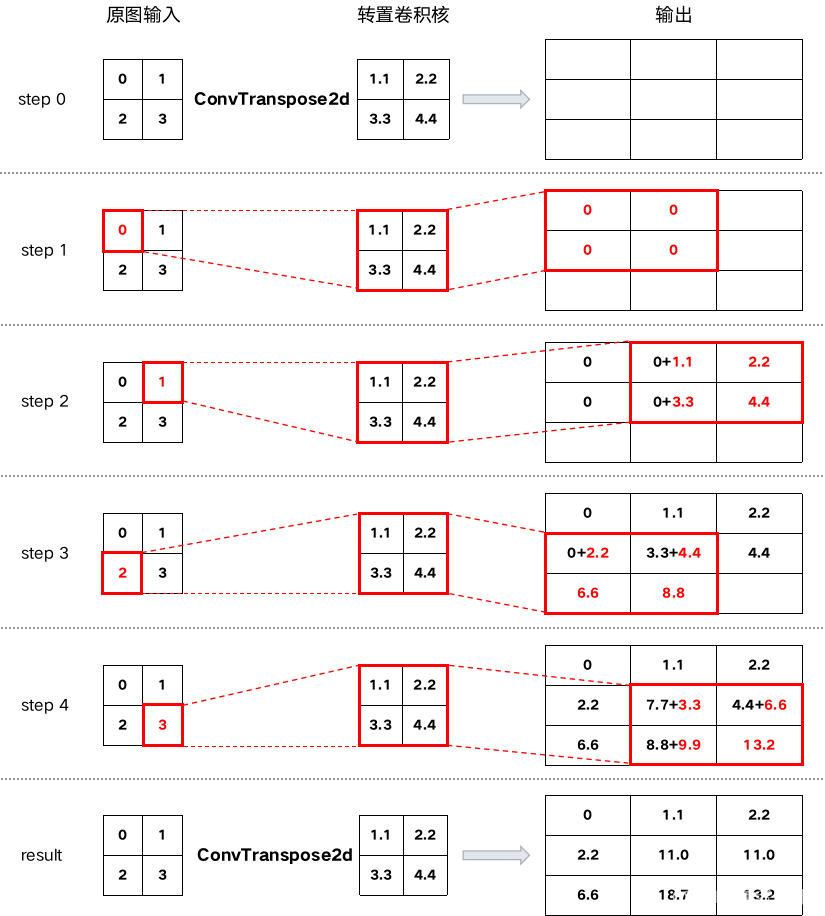
容易看出，经历转置卷积后特征图会扩大，即上采样。使用代码验算：

import torchinput = torch.tensor([[[[0,1],[2,3]]]],dtype=torch.float32)ConvTrans = torch.nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=2, stride=1, padding=0, output_padding=0,dilation=1,bias=False)
ConvTrans.weight = torch.nn.Parameter(torch.tensor([[[[ 1.1, 2.2],[ 3.3, 4.4]]]], dtype=torch.float32,requires_grad=True))print(ConvTrans(input))

输出为：

tensor([[[[ 0.0000,  1.1000,  2.2000],[ 2.2000, 11.0000, 11.0000],[ 6.6000, 18.7000, 13.2000]]]], grad_fn=<ConvolutionBackward0>)

3.2 调整stride

把stride调整为2后，计算过程如下：

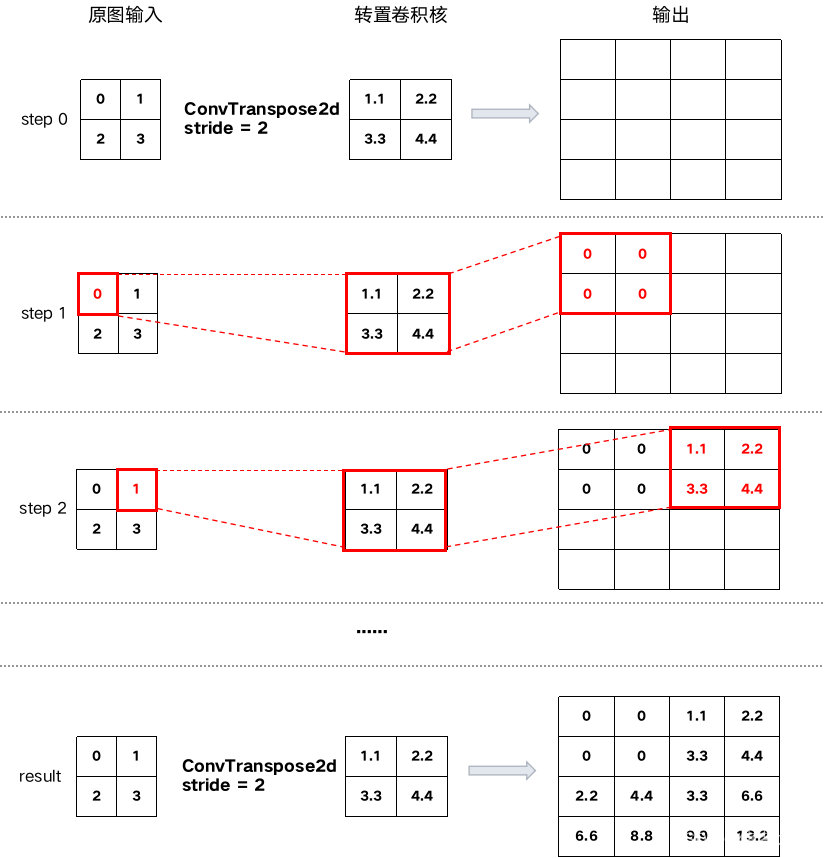
如果stride过大，则会在跳过的位置补0。例如上面的计算过程中，如果stride = 3输出则为：

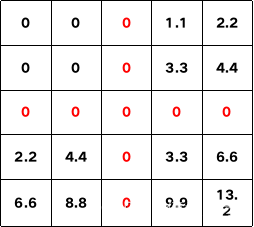
注意，这里stride可以指定为tuple，即让横向和纵向的stride不一样，例如(1, 2)，但其计算思路不变，这里直接用代码计算结果（懒得再画过程图了）：

import torchinput = torch.tensor([[[[0,1],[2,3]]]],dtype=torch.float32)ConvTrans = torch.nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=2, stride=(1,2), padding=0, output_padding=0,dilation=1,bias=False)
ConvTrans.weight = torch.nn.Parameter(torch.tensor([[[[ 1.1, 2.2],[ 3.3, 4.4]]]], dtype=torch.float32,requires_grad=True))print(ConvTrans(input))

输出为：

tensor([[[[ 0.0000,  0.0000,  1.1000,  2.2000],[ 2.2000,  4.4000,  6.6000, 11.0000],[ 6.6000,  8.8000,  9.9000, 13.2000]]]],grad_fn=<ConvolutionBackward0>)

3.3 调整dilation

这个过程非常简单，可以分为2步：

1. 把卷积核进行dilation（爆炸）处理
2. 进行3.1基本过程

即：

代码验算过程如下：

import torchinput = torch.tensor([[[[0,1],[2,3]]]],dtype=torch.float32)ConvTrans_dilation2 = torch.nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=2, stride=1, padding=0, output_padding=0,dilation=2,bias=False)
ConvTrans_dilation2.weight = torch.nn.Parameter(torch.tensor([[[[ 1.1, 2.2],[ 3.3, 4.4]]]], dtype=torch.float32,requires_grad=True))print(ConvTrans_dilation2(input))ConvTrans_dilation1 = torch.nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=2, stride=1, padding=0, output_padding=0,dilation=1,bias=False)
ConvTrans_dilation1.weight = torch.nn.Parameter(torch.tensor([[[[1.1, 0, 2.2],[0, 0, 0],[3.3, 0, 4.4]]]], dtype=torch.float32,requires_grad=True))   #对卷积核进行dilationprint(ConvTrans_dilation1(input))
print(ConvTrans_dilation2(input) == ConvTrans_dilation1(input))

输出为：

tensor([[[[ 0.0000,  1.1000,  0.0000,  2.2000],[ 2.2000,  3.3000,  4.4000,  6.6000],[ 0.0000,  3.3000,  0.0000,  4.4000],[ 6.6000,  9.9000,  8.8000, 13.2000]]]],grad_fn=<ConvolutionBackward0>)
tensor([[[[ 0.0000,  1.1000,  0.0000,  2.2000],[ 2.2000,  3.3000,  4.4000,  6.6000],[ 0.0000,  3.3000,  0.0000,  4.4000],[ 6.6000,  9.9000,  8.8000, 13.2000]]]],grad_fn=<ConvolutionBackward0>)
tensor([[[[True, True, True, True],[True, True, True, True],[True, True, True, True],[True, True, True, True]]]])

3.4 调整padding

这是一个下采样的过程，会减少输出size。具体计算方法也很简单：给输出数据减去padding圈。基于3.1基本过程举例说明padding = 1的情况如下：

3.5 调整output_padding

这个参数用于给最终输出补0，output_padding必须要比stride或者dilation小。需要注意的是output_padding补0只能补半圈，如下：

我也想不明白为什么不是补一整圈？

4. 应用实例

在实际使用中，nn.ConvTranspose2d 可以嵌入到神经网络结构中，用于实现上采样、特征图尺寸放大或生成与输入尺寸相似的输出。以下是一个简单的使用示例：

import torch
import torch.nn as nn# 定义一个包含转置卷积层的简单模型
class TransposedConvModel(nn.Module):def __init__(self, in_channels=32, out_channels=64, kernel_size=4, stride=2, padding=1, output_padding=0):super().__init__()self.conv_transpose = nn.ConvTranspose2d(in_channels=in_channels,out_channels=out_channels,kernel_size=kernel_size,stride=stride,padding=padding,output_padding=output_padding,bias=True)def forward(self, x):return self.conv_transpose(x)# 实例化模型并应用到输入数据
model = TransposedConvModel()
input_tensor = torch.randn(1, 32, 16, 16)  # (batch_size, in_channels, height, width)
output = model(input_tensor)
print("Output shape:", output.shape)

输出为：

Output shape: torch.Size([1, 64, 32, 32])

5. 总结

nn.ConvTranspose2d 是 PyTorch 中用于实现二维转置卷积的关键模块，它通过逆向的卷积操作实现了特征图的上采样和空间维度的扩大。

正确理解和配置其参数（如 kernel_size、stride、padding、output_padding 等），可以帮助开发者构建出适应特定任务需求的神经网络架构，特别是在图像生成、超分辨率、语义分割等需要从低分辨率特征恢复到高分辨率输出的应用场景中发挥关键作用。通过实践和调整这些参数，研究人员和工程师能够灵活地设计和优化基于转置卷积的深度学习模型。