A 构造相同颜色的正方形
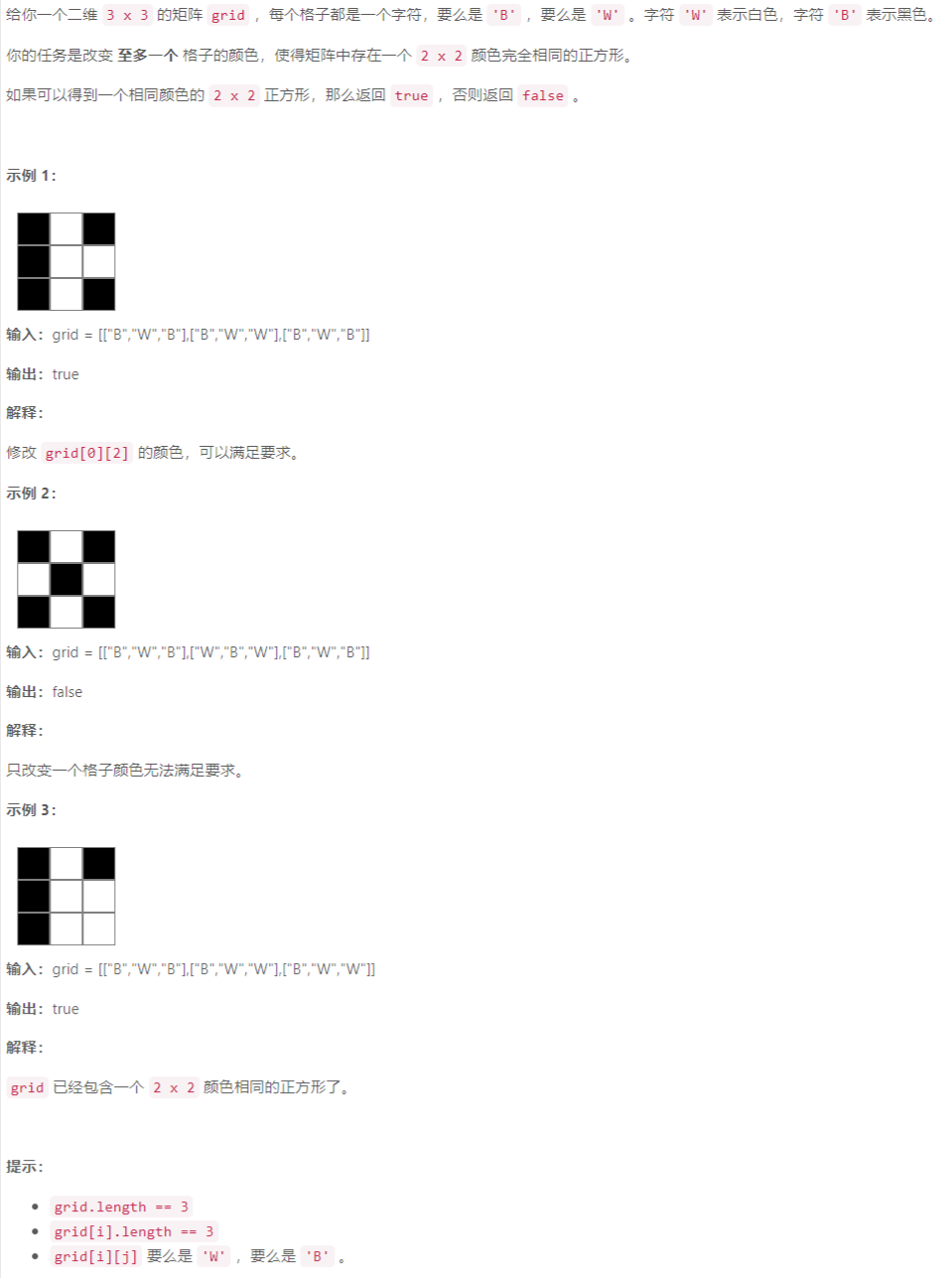
枚举:枚举每个 3 × 3 3\times 3 3×3的矩阵,判断是否满足条件
class Solution {public:bool canMakeSquare(vector<vector<char>>& grid) {for (int i = 0; i < 2; i++)for (int j = 0; j < 2; j++) {int c1 = 0, c2 = 0;for (int r = 0; r < 2; r++)for (int c = 0; c < 2; c++)if (grid[i + r][j + c] == 'B')c1++;elsec2++;if (max(c1, c2) >= 3)return true;}return false;}
};
B 直角三角形
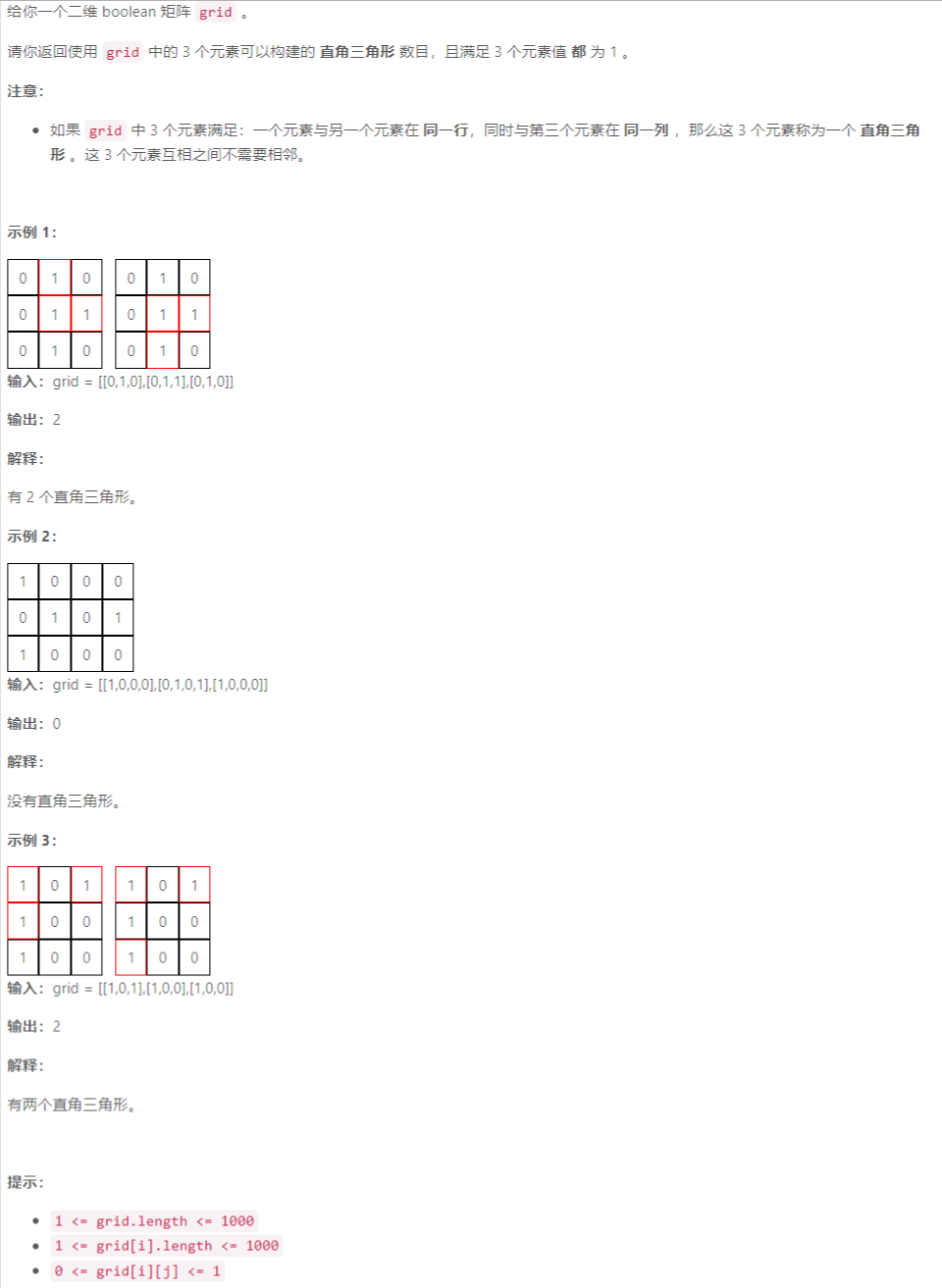
枚举:记录各行各列的 1 1 1 的数目,然后枚举每个直接三角形的直角所在的位置 g r i d [ i ] [ j ] grid[i][j] grid[i][j]
class Solution {public:long long numberOfRightTriangles(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<int> row(m), col(n);for (int i = 0; i < m; i++)for (int j = 0; j < n; j++) {row[i] += grid[i][j];col[j] += grid[i][j];}long long res = 0;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)if (grid[i][j])res += 1LL * (row[i] - 1) * (col[j] - 1);return res;}
};
C 找出所有稳定的二进制数组 I

动态规划:设 p [ i ] [ j ] [ t a i l ] p[i][j][tail] p[i][j][tail] 为含有 i i i 个 0 0 0 和 j j j 个 1 1 1 且以 t a i l tail tail 为结尾的稳定二进制数组的个数,可以枚举其全为 t a i l tail tail 的后缀数组的可能长度来进行状态转移
class Solution {public:using ll = long long;ll mod = 1e9 + 7;int numberOfStableArrays(int zero, int one, int limit) {ll p[zero + 1][one + 1][2]; memset(p, 0, sizeof(p));for (int cz = 1; cz <= zero && cz <= limit; ++cz)p[cz][0][0] = 1;for (int co = 1; co <= one && co <= limit; ++co)p[0][co][1] = 1;for (int i = 0; i <= zero; i++) {for (int j = 0; j <= one; j++) {for (int last = 1; last <= limit; last++) {//全为tail的后缀数组的长度为lastif (i - last >= 0)p[i][j][0] = (p[i][j][0] + p[i - last][j][1]) % mod;if (j - last >= 0)p[i][j][1] = (p[i][j][1] + p[i][j - last][0]) % mod;}}}return ((p[zero][one][0] + p[zero][one][1]) % mod + mod) % mod;}
};
D 找出所有稳定的二进制数组 II

动态规划:设 p [ i ] [ j ] [ t a i l ] p[i][j][tail] p[i][j][tail] 为含有 i i i 个 0 0 0 和 j j j 个 1 1 1 且以 t a i l tail tail 为结尾的稳定二进制数组的个数,枚举其全为 t a i l tail tail 的后缀数组的可能长度来进行状态转移,可以通过维护两个前缀和来优化状态转移的时间复杂度
class Solution {public:using ll = long long;ll mod = 1e9 + 7;int numberOfStableArrays(int zero, int one, int limit) {ll p[zero + 1][one + 1][2]; ll ps0[zero + 1][one + 1];ll ps1[zero + 1][one + 1];memset(p, 0, sizeof(p));memset(ps0, 0, sizeof(ps0));memset(ps1, 0, sizeof(ps1));for (int i = 1; i <= zero && i <= limit; ++i) {p[i][0][0] = 1;ps0[i][0] = 1;}for (int j = 1; j <= one && j <= limit; ++j) {p[0][j][1] = 1;ps1[0][j] = 1;}for (int i = 0; i <= zero; i++) {for (int j = 0; j <= one; j++) {// [max(0,i-limit),i-1]if (int l = max(0, i - limit), r = i - 1; l <= r)p[i][j][0] += l != 0 ? (ps1[r][j] - ps1[l - 1][j]) % mod : ps1[r][j];if (int l = max(0, j - limit), r = j - 1; l <= r)p[i][j][1] += l != 0 ? (ps0[i][r] - ps0[i][l - 1]) % mod : ps0[i][r];if (j)ps0[i][j] = (ps0[i][j - 1] + p[i][j][0]) % mod;if (i)ps1[i][j] = (ps1[i - 1][j] + p[i][j][1]) % mod;}}return ((p[zero][one][0] + p[zero][one][1]) % mod + mod) % mod;}
};


)


)
前置技能)







![[Linux]如何在Ubuntu 22.04系統安裝Node-red?](http://pic.xiahunao.cn/[Linux]如何在Ubuntu 22.04系統安裝Node-red?)

)
)

