文章目录
- 监督学习
- 线性回归
- 逻辑回归
- 决策树
- 支持向量机
- 朴素贝叶斯
- 集成学习
- Bagging
- Boosting
- 无监督学习
- 主成分分析
- KMeans聚类
- 缺失值和分类数据处理
- 处理缺失数据
- 分类数据转化为OneHot编码
- 葡萄酒数据集示例
机器学习的流程如下所示:
![![[Pasted image 20240507152730.png]]](https://img-blog.csdnimg.cn/direct/86131d95a6fb4ba4964c33df6bd8dd84.png)
具体又可以分为以下五个步骤:
- 明确目标:在机器学习项目中,首先需要明确业务目标和机器学习目标。业务目标是指希望机器学习模型能够帮助实现的具体业务需求,例如提高销售额、降低风险等。机器学习目标则是指需要通过机器学习模型来解决的具体问题,例如分类、回归、聚类等。在明确了目标之后,需要根据目标来选择适当的机器学习任务和评估指标。
- 收集数据:在明确了目标之后,需要收集相关的数据用于机器学习模型的训练和测试。数据可以来自于各种来源,例如数据库、文本文件、网页等。在收集数据时,需要确保数据的质量和量,同时也需要考虑数据的可用性和合法性。
- 数据探索和数据预处理:在收集到数据之后,需要对数据进行探索和预处理。数据探索是指通过统计学和可视化等手段对数据进行分析,了解数据的特点和规律。数据预处理是指对数据进行清洗、转换、降维等操作,使其满足机器学习模型的要求。在这一步骤中,还需要对数据进行分割,将其分为训练集、验证集和测试集。
- 模型选择:在数据预处理之后,需要选择适合的机器学习模型来解决具体的问题。模型选择需要考虑多方面的因素,例如模型的复杂度、训练时间、预测精度等。在选择模型时,还需要考虑模型的可解释性和可扩展性。
- 模型评估:在选择好模型之后,需要对模型进行评估,以确定其在实际应用中的表现。模型评估需要使用适当的评估指标,例如准确率、精确率、召回率等。在评估模型时,还需要考虑模型的泛化能力和鲁棒性。通过对模型进行评估,可以进一步优化模型,提高其预测精度和可靠性。一般使用
K折交叉验证来评估模型
根据问题类型选择损失函数
| 问题类型 | 损失函数 | 评估指标 |
|---|---|---|
| 回归模型 | MSE | MSE,MAE |
| SVM | hinge | Accuracy,Precision,Recall |
| 二分类模型 | BinaryCrossentropy | Accuracy,Precision,Recall |
| 多分类模型 | CategoricalCrossentropy | TopKCategoricalCrossentropy |
监督学习
监督学习通俗来讲指的就是有y的数据集
线性回归
线性回归是最简单,最普通的一种做法, 机器学习中的线性回归非常简单和粗暴,不同于统计模型中有各个变量的P值什么的,机器学习中的线性回归只有一个 parameters 还有一个 score
线性回归公式非常简单: f ( x ) = w 1 x 1 + w 2 x 3 + ⋯ + w n x n + b f(x)=w_1x_1+w_2x_3+\dots+w_nx_n+b f(x)=w1x1+w2x3+⋯+wnxn+b
在sklearn导入:from sklearn.linear_model import LinearRegression
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression## 这里使用 make_regression 创建回归数据集
X, y = make_regression(n_samples=1000, n_features=10, bias=1.2, noise=10)## 因为这里添加了bias,所以会有常数项,而LinearRegression默认包含常数项的 fit_intercept=True
linear_model = LinearRegression(fit_intercept=True)## 训练
linear_model.fit(X, y)## 得到模型的系数和常数
linear_model.coef_, linear_model.intercept_
要深入探究线性回归,可以对普通的loss做一些变换,得到不同的线性回归模型:Ridge,Lasso,ElasticNet
首先是 L 1 L_1 L1惩罚: L 1 ( w ) = ∣ ∣ w ∣ ∣ 1 = ∑ ∣ w i ∣ L_1(w) = ||w||_1=\sum|w_i| L1(w)=∣∣w∣∣1=∑∣wi∣
其次是 L 2 L_2 L2惩罚: L 2 ( w ) = ∣ ∣ w ∣ ∣ 2 = ∑ w i 2 L_2(w)=||w||_2=\sum w_i^2 L2(w)=∣∣w∣∣2=∑wi2
Ridge的loss L = ∑ ( f ( x i ) − y i ) 2 + α L 1 ( w 2 ) \mathcal{L}=\sum (f(x_i)-y_i)^2 + \alpha L_1(w_2) L=∑(f(xi)−yi)2+αL1(w2)
Lasso的loss L = ∑ ( f ( x i ) − y i ) 2 + α L 1 ( w 1 ) \mathcal{L}=\sum (f(x_i)-y_i)^2 + \alpha L_1(w_1) L=∑(f(xi)−yi)2+αL1(w1)
ElasticNet的loss L = ∑ ( f ( x i ) − y i ) 2 + α L 1 ( w ) + β L 2 ( w ) \mathcal{L}=\sum (f(x_i)-y_i)^2 + \alpha L_1(w) + \beta L_2(w) L=∑(f(xi)−yi)2+αL1(w)+βL2(w)
这里统计学的书籍会具体讲一下适用于哪些数据特征的模型,从损失函数中可以看到,主要是为了防止过拟合问题
逻辑回归
逻辑回归是用来处理二分类问题的模型,类似的模型还有Probit模型,不同的是逻辑回归使用sigmoid函数来处理概率,而Probit使用正态分布累计密度函数来处理概率模型。
sigmoid函数如下: f ( z ) = 1 1 + e − z f(z)=\frac{1}{1+e^{-z}} f(z)=1+e−z1
正态分布累计密度如下: f ( z ) = 1 2 π ∫ − ∞ z e − t 2 2 d t f(z)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^ze^{-\frac{t^2}{2}}dt f(z)=2π1∫−∞ze−2t2dt
很明显,两个模型都是把值映射在0-1范围内,但prob涉及到积分,导致运算速度不如逻辑回归,所以逻辑回归更为通用。这里的 z z z 相当于线性回归中的 y y y 值。
这里loss涉及到了一种类似于期望处理方法,如下表所示:
| loss | l a b e l t r u e = 0 label_{true}=0 labeltrue=0 | l a b e l t r u e = 1 label_{true}=1 labeltrue=1 |
|---|---|---|
| l a b e l p r e d = 0 label_{pred}=0 labelpred=0 | 0 | α \alpha α |
| l a b e l p r e d = 1 label_{pred}=1 labelpred=1 | β \beta β | 0 |
由条件概率可得:
P ( l a b e l p r e d = 0 ) = P ( l a b e l p r e d = 0 ∣ l a b e l t r u e = 0 ) P ( l a b e l t r u e = 0 ) + P ( l a b e l p r e d = 0 ∣ l a b e l t r u e = 1 ) P ( l a b e l t r u e = 1 ) P(label_{pred}=0)=P(label_{pred}=0|label_{true}=0)P(label_{true}=0) + P(label_{pred}=0|label_{true}=1)P(label_{true}=1) P(labelpred=0)=P(labelpred=0∣labeltrue=0)P(labeltrue=0)+P(labelpred=0∣labeltrue=1)P(labeltrue=1)
由于 P ( l a b e l t r u e = 0 ) P(label_{true}=0) P(labeltrue=0), P ( l a b e l t r u e = 1 ) P(label_{true}=1) P(labeltrue=1)只能等于 0,1,并且是已知的;所以 P ( l a b e l p r e d = 0 ) = P ( l a b e l p r e d = 0 ∣ l a b e l t r u e = 0 ) P(label_{pred}=0)=P(label_{pred}=0|label_{true}=0) P(labelpred=0)=P(labelpred=0∣labeltrue=0),或者 P ( l a b e l p r e d = 0 ) = P ( l a b e l p r e d = 0 ∣ l a b e l t r u e = 1 ) P(label_{pred}=0)=P(label_{pred}=0|label_{true}=1) P(labelpred=0)=P(labelpred=0∣labeltrue=1);同理 P ( l a b e l p r e d = 1 ) = P ( l a b e l p r e d = 1 ∣ l a b e l t r u e = 0 ) P(label_{pred}=1)=P(label_{pred}=1|label_{true}=0) P(labelpred=1)=P(labelpred=1∣labeltrue=0),或者 P ( l a b e l p r e d = 1 ) = P ( l a b e l p r e d = 1 ∣ l a b e l t r u e = 1 ) P(label_{pred}=1)=P(label_{pred}=1|label_{true}=1) P(labelpred=1)=P(labelpred=1∣labeltrue=1);
L = α P ( l a b e l p r e d = 0 ∣ l a b e l t r u e = 1 ) P ( l a b e l t r u e = 1 ) + β P ( l a b e l p r e d = 1 ∣ l a b e l t r u e = 0 ) P ( l a b e l t r u e = 0 ) = α [ 1 − P ( l a b e l p r e d = 0 ∣ l a b e l t r u e = 1 ) ] [ 1 − P ( l a b e l t r u e = 0 ) ] + β P ( l a b e l p r e d = 1 ∣ l a b e l t r u e = 0 ) P ( l a b e l t r u e = 0 ) = α ( 1 − y ) ( 1 − p ( x ) ) + β y p ( x ) \begin{align} \mathcal{L} &= \alpha P(label_{pred}=0|label_{true}=1)P(label_{true}=1) + \beta P(label_{pred}=1|label_{true}=0)P(label_{true}=0) \\ &=\alpha [1-P(label_{pred}=0|label_{true}=1)][1-P(label_{true}=0)] + \beta P(label_{pred}=1|label_{true}=0)P(label_{true}=0) \\ &= \alpha (1-y)(1-p(x)) + \beta yp(x) \end{align} L=αP(labelpred=0∣labeltrue=1)P(labeltrue=1)+βP(labelpred=1∣labeltrue=0)P(labeltrue=0)=α[1−P(labelpred=0∣labeltrue=1)][1−P(labeltrue=0)]+βP(labelpred=1∣labeltrue=0)P(labeltrue=0)=α(1−y)(1−p(x))+βyp(x)
很明显,当 α \alpha α 和 β \beta β 相等且为1的时候,惩罚为 L = ∑ y i p ( x i ) + ( 1 − y i ) p ( x i ) \mathcal{L}=\sum y_ip(x_i) +(1-y_i)p(x_i) L=∑yip(xi)+(1−yi)p(xi)
以上的公式很出名,但是在实际应用中,把这一类分为另一类,和把另一类分为这一类的损失是不同的,所以根据情况自定义;
在sklearn导入:from sklearn.linear_model import LogisticRegression
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification## 这里使用 make_classification 创建分类数据集
X, y = make_classification(n_samples=1000, n_features=10, n_classes=2)## 建立模型
log_reg = LogisticRegression()## 模型训练
log_reg.fit(X, y)## 得到模型的系数和常数
log_reg.intercept_, log_reg.coef_
决策树
决策树有三种出名的算法:ID3,C4.5,CART 太多了,详细可以看周志华老师的机器学习介绍,这里做一下代码使用实例
![![[Pasted image 20240507214917.png]]](https://img-blog.csdnimg.cn/direct/fe8d68bf367e4cdc8268acbf5774d370.png)
利用决策树来解决回归
from sklearn.datasets import load_diabetes
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor## 导入数据
X, y = load_diabetes(return_X_y=True)## 选择模型
regressor = DecisionTreeRegressor(random_state=0)## 训练并使用交叉验证打分
cross_val_score(regressor, X, y, cv=10)
利用决策树来解决分类
from sklearn.datasets import load_diabetes
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor## 导入数据
X, y = load_iris(return_X_y=True)## 选择模型
clf = DecisionTreeClassifier(random_state=0)## 训练并使用交叉验证打分
cross_val_score(clf, X, y, cv=10)
支持向量机
支持向量分类的核心思想:找一个超平面把两类数据尽可能给分割开来
支持向量回归的核心思想:找两个平行的超平面把数据尽可能靠拢
![![[Pasted image 20240507215503.png]]](https://img-blog.csdnimg.cn/direct/8e054eb9b3ec43d88329b5d9889ece1e.png)
SVR
from sklearn.svm import SVR
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
import numpy as npn_samples, n_features = 10, 5rng = np.random.RandomState(0)
y = rng.randn(n_samples)
X = rng.randn(n_samples, n_features)regr = make_pipeline(StandardScaler(), SVR(C=1.0, epsilon=0.2))
regr.fit(X, y)
SVC
from sklearn.svm import SVC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
import numpy as npX = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])clf = make_pipeline(StandardScaler(), SVC(gamma='auto'))
clf.fit(X, y)
朴素贝叶斯
朴素贝叶斯假设:属性条件独立,其核心思想 p ( c ∣ x ) = p ( x ∣ c ) p ( c ) p ( x ) p(c|x)=\frac{p(x|c)p(c)}{p(x)} p(c∣x)=p(x)p(x∣c)p(c)
其中 c c c 表示类别,利用计算 p ( x ∣ c ) p ( c ) p(x|c)p(c) p(x∣c)p(c) 的方式去计算 p ( c ∣ x ) p(c|x) p(c∣x) ,这里的 p ( x ) p(x) p(x) 由于做比较就可以忽略;
由于属性条件独立,有 p ( x ∣ c ) = p ( ( x 1 , x 2 , … , x m ) ∣ c ) = ∏ p ( x i ∣ c ) p(x|c)=p((x_1,x_2,\dots,x_m)|c)=\prod p(x_i|c) p(x∣c)=p((x1,x2,…,xm)∣c)=∏p(xi∣c)
最后判别类别有: a r g m a x p ( c ) ∏ p ( x i ∣ c ) argmax \ \ p(c)\prod p(x_i|c) argmax p(c)∏p(xi∣c)
import numpy as np
from sklearn.naive_bayes import CategoricalNBrng = np.random.RandomState(1)
X = rng.randint(5, size=(6, 100))
y = np.array([1, 2, 3, 4, 5, 6])clf = CategoricalNB()
clf.fit(X, y)
集成学习
集成学习思想类似于:三个臭皮匠顶一个诸葛亮 ,通过总结不同模型的输出结果得到一个最终的结果
集成学习有两种典型的算法:装袋算法(Bagging) 和 提升分类器(Boosting)
Boosting:个体学习器之间存在强依赖关系,必须串行生成的序列化方法。
Bagging:个体学习器之间存在弱依赖关系,可同时生成的并行化方法。
Bagging
- 采样:从原始数据集中,使用Bootstrap方法进行有放回的抽样,生成新的训练子集。这意味着每个子集都是通过随机选择原始数据集中的样本而创建的,且一个样本在一次抽样中可以被重复选中多次,而有些样本可能一次都不会被选中。通常,这些子集的大小与原始数据集相同。
- 训练:对于每一个由Bootstrap生成的子集,使用一个基础学习算法(如决策树、线性回归等)独立地训练一个模型。由于各个子集之间是独立的,这些模型的训练过程可以并行进行。
- 预测: 对于分类任务,所有模型的预测结果将通过投票的方式汇总,即每个模型对测试样本的预测类别进行投票,最终得票最多的类别作为Bagging集成的预测结果。对于回归任务,所有模型的预测值将被简单平均(或加权平均),以得到最终的预测值。
Bagging通过结合多个模型的预测来减少单一模型可能引入的方差,从而提高整体模型的稳定性和泛化能力。这种方法特别有效于那些具有高方差的学习算法。通过上述步骤,Bagging能够有效地减少模型的过拟合风险,并在很多情况下显著提升模型的性能。随机森林(Random Forest)是Bagging思想的一个典型应用,它在构建决策树时不仅使用Bootstrap采样,还加入了特征随机选择的机制,进一步增强了模型的多样性与泛化能力。
Boosting
- 先从初始训练集训练处一个基学习器;
- 再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的样本在后续受到更多的关注;
- 基于调整后的样本分布来训练下一个基学习器;
- 一直重复上述步骤,直到基学习器的个数达到train前的指定数T,然后将这T个基学习器进行加权;
![![[无标题.png]]](https://img-blog.csdnimg.cn/direct/77a5f82dcf444467beae24d7eb29f55e.png)
基于Boosting思想的算法主要有:AdaBoost,GBDT,XGBoost
无监督学习
主成分分析
主成分分析 PCA 是一种降维的算法,还有一种叫 TSNE
PCA的基本思想是通过旋转的方式,把轴转换到方差最大的方向,然后选取方差大小前面的几个轴
import numpy as np
from sklearn.decomposition import PCAX = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=2)
pca.fit(X)
KMeans聚类
from sklearn.cluster import KMeans
import numpy as npX = np.array([[1, 2], [1, 4], [1, 0],[10, 2], [10, 4], [10, 0]])
kmeans = KMeans(n_clusters=2, random_state=0, n_init="auto").fit(X)## 查看x对应的label
kmeans.labels_
当数据量较大时,可以使用 MiniBatchKMeans 进行计算,这样不用带入所有数据
缺失值和分类数据处理
处理缺失数据
处理缺失数据主要在sklearn.impute这个包内,impute.SimpleImputer,impute.IterativeImputer,impute.MissingIndicator,impute.KNNImputer
import pandas as pd
from io import StringIO
import numpy as np
from sklearn.impute import SimpleImputercsv_data = '''A,B,C,D
1.0,2.0,3.0,4.0
5.0,6.0,,8.0
10.0,11.0,12.0,'''## 读取数据
df = pd.read_csv(StringIO(csv_data))## 观察每一列的缺失值数量
df.isnull().sum()## 缺失值使用均值填充
imr = SimpleImputer(missing_values=np.nan, strategy='mean')
imputed_data = imr.fit_transform(df)
imputed_data
分类数据转化为OneHot编码
import pandas as pd
df = pd.DataFrame([['green', 'M', 10.1, 'class1'], ['red', 'L', 13.5, 'class2'], ['blue', 'XL', 15.3, 'class1']])df.columns = ['颜色', '型号', '价格', '类别']size_mapping = {'XL': 3,'L': 2,'M': 1}df['型号'] = df['型号'].map(size_mapping)## 获取OneHot编码
pd.get_dummies(df[['价格', '颜色', '型号', '类别']], drop_first=True)
get_dummies 函数会把所有的字符变量都变成OneHot编码,但是很明显,n个维度只能有n-1个编码,否则会造成多重共线性,不可取,所以一般要使用 drop_first
葡萄酒数据集示例
准备数据,这里使用 sklearn.datasets 中的 wine 数据集
import pandas as pd
import numpy as np
from sklearn.datasets import load_winedata = load_wine()
X, y, feature_names = data['data'], data['target'], data['feature_names']
df_wine = pd.DataFrame(np.c_[X, y], columns=feature_names + ['class'])
切分训练集和测试集,标准化
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)stdsc = StandardScaler()
X_train_std = stdsc.fit_transform(X_train)
X_test_std = stdsc.transform(X_test)
这里使用逻辑回归尝试做一个模型,发现效果还不错,这里的C是惩罚系数的倒数
from sklearn.linear_model import LogisticRegressionlr = LogisticRegression(penalty='l1', C=0.1,solver='liblinear')
lr.fit(X_train_std, y_train)
print('Training accuracy:', lr.score(X_train_std, y_train))
print('Test accuracy:', lr.score(X_test_std, y_test))# Training accuracy: 0.9838709677419355
# Test accuracy: 0.9814814814814815
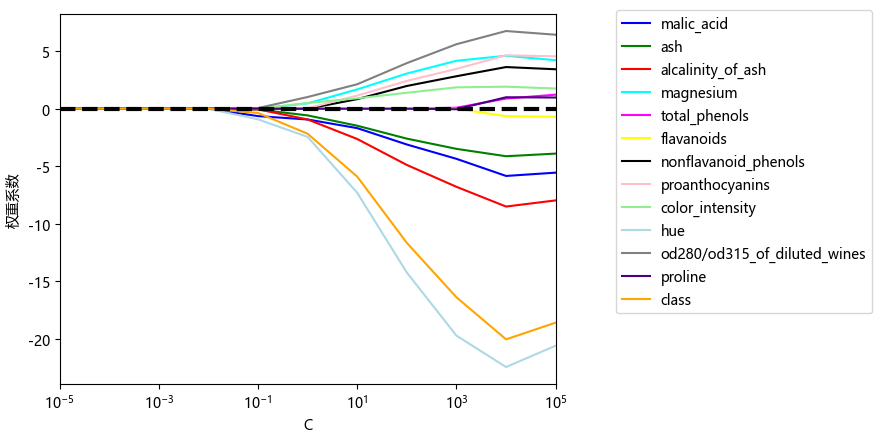
接着通过更改惩罚系数,观察逻辑回归模型参数的变化过程
weights, params = [], []
for c in np.arange(-4, 6):lr = LogisticRegression(penalty='l1', C=10.**c, solver='liblinear')lr.fit(X_train_std, y_train)weights.append(lr.coef_[1])params.append(10.**c)weights = np.array(weights)
画图,由于x轴是对数距离,所以需要放缩 plt.xscale('log')
import matplotlib.pyplot as pltplt.rcParams['font.sans-serif']=['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False fig = plt.figure()
ax = plt.subplot(111)colors = ['blue', 'green', 'red', 'cyan', 'magenta', 'yellow', 'black', 'pink', 'lightgreen', 'lightblue', 'gray', 'indigo', 'orange']for column, color in zip(range(weights.shape[1]), colors):plt.plot(params, weights[:, column], label=df_wine.columns[column+1], color=color)## 在y=0上画一根--
plt.axhline(0, color='black', linestyle='--', linewidth=3)## 限制x轴为[10^-5, 10^5]
plt.xlim([10**(-5), 10**5])plt.ylabel('权重系数')
plt.xlabel('C')## !!! x轴的距离使用对数距离
plt.xscale('log')## 设置pic的legend
plt.legend(loc='upper left')
ax.legend(loc='upper center', bbox_to_anchor=(1.38, 1.03),ncol=1, fancybox=True)
最后进行特征选择,分值的方式有两种:AIC 和 BIC;选择的方式有三种: 前向选择,后向选择以及逐步选择。这里是根据score的分值,使用后向选择的方式对变量进行剔除。
from sklearn.base import clone
from itertools import combinations
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_scoreclass SBS():def __init__(self, estimator, k_features, scoring=accuracy_score,test_size=0.25, random_state=1):self.scoring = scoringself.estimator = clone(estimator)self.k_features = k_featuresself.test_size = test_sizeself.random_state = random_statedef fit(self, X, y):X_train, X_test, y_train, y_test = \train_test_split(X, y, test_size=self.test_size, random_state=self.random_state)dim = X_train.shape[1]self.indices_ = tuple(range(dim))self.subsets_ = [self.indices_]score = self._calc_score(X_train, y_train, X_test, y_test, self.indices_)self.scores_ = [score]while dim > self.k_features:scores = []subsets = []for p in combinations(self.indices_, r=dim-1):score = self._calc_score(X_train, y_train, X_test, y_test, p)scores.append(score)subsets.append(p)best = np.argmax(scores)self.indices_ = subsets[best]self.subsets_.append(self.indices_)dim -= 1self.scores_.append(scores[best])self.k_score_ = self.scores_[-1]return selfdef transform(self, X):return X[:, self.indices_]def _calc_score(self, X_train, y_train, X_test, y_test, indices):self.estimator.fit(X_train[:, indices], y_train)y_pred = self.estimator.predict(X_test[:, indices])score = self.scoring(y_test, y_pred)return score
接着使用KNN模型作为分类器
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as pltknn = KNeighborsClassifier(n_neighbors=2)# 选择特征
sbs = SBS(knn, k_features=1)
sbs.fit(X_train_std, y_train)# 可视化特征子集的性能
k_feat = [len(k) for k in sbs.subsets_]plt.plot(k_feat, sbs.scores_, marker='o')
plt.ylim([0.7, 1.1])
plt.ylabel('Accuracy')
plt.xlabel('Number of features')
plt.grid()
plt.tight_layout()
plt.show()
得到结果:
![![[Pasted image 20240508000139.png]]](https://img-blog.csdnimg.cn/direct/96cc9c6d59ec4667b6be40b0bc238b19.png)
使用随机森林获取特征重要性
from sklearn.ensemble import RandomForestClassifierfeat_labels = feature_namesforest = RandomForestClassifier(n_estimators=1000,random_state=0,n_jobs=-1)forest.fit(X_train, y_train)
importances = forest.feature_importances_indices = np.argsort(importances)[::-1]plt.title('Feature Importances')
plt.bar(range(X_train.shape[1]), importances[indices],color='lightblue', align='center')plt.xticks(range(X_train.shape[1]), feat_labels, rotation=90)
plt.xlim([-1, X_train.shape[1]])
plt.tight_layout()
plt.show()
![![[Pasted image 20240508000341.png]]](https://img-blog.csdnimg.cn/direct/66c570d60d9849dd8546314ac7b664a1.png)

![[C++核心编程-04]----C++类和对象之封装](http://pic.xiahunao.cn/[C++核心编程-04]----C++类和对象之封装)

)




【保姆级教学】【2023.10月最新版】)


![[法规规划|数据概念]金融行业数据资产和安全管理系列文件解析(3)](http://pic.xiahunao.cn/[法规规划|数据概念]金融行业数据资产和安全管理系列文件解析(3))



)



