下面是对双指针算法的题目总结和归纳，有需要借鉴即可。

1.移动零

题目链接：LINK

题解：

• 思路①：暴力求解

  • 详述：碰到0，后面所有数字往前挪动一位；碰到非0不用管。
  • 时间复杂度：O(N^2)

• 思路②：双指针算法

  • 详述：定义两个指针pcur和pdest，pcur起始位置在0下标处，用来遍历数组；pdest起始位置在-1.用来保留要交换数字的下标；如果pcur遇到非0，那就dest与pcur位置的值进行交换，如果是0，pcur继续向后走，不做处理。
  • 时间复杂度：O(N)

class Solution {
public:void Swap(int& x,int& y){int temp = x;x = y;y = temp;}void moveZeroes(vector<int>& nums) {int pcur = 0;int pdest = -1;while(pcur < nums.size())//遍历完成就结束{//不是0，我们就换一下if(nums[pcur] != 0){Swap(nums[++pdest],nums[pcur]);}        pcur++;}}
};

2.复写零

题目链接：LINK

题解：

• 思路①：暴力求解
  • 详述：定义一个指针，一个pcur，扫描，如果pcur找到的是非0，那就不用管，；如果pcur找到的是0，那就把该数组所有元素往后移动一位，并且把该位置置为0。
  • 复杂度：O(N^2)
• 思路②：双指针法
  • 详述：定义两个指针，先大致模拟一下最后pcur和dest最后结果在哪，然后从后向前进行复写。
  • 复杂度：O(N)

class Solution {
public:void duplicateZeros(vector<int>& arr) {int cur = 0,dest = -1,n = arr.size();//1.先找到cur和dest应该指向的位置while(cur < n){if(arr[cur])//非0{dest++;}else{dest+=2;}if(dest>=n-1)//终止条件：dest到达最后一个地方或者说超出了{break;}cur++;}//2.处理一下特殊情况if(dest == n){arr[--dest] = 0;cur--;dest--;}//3.依次赋值while(cur>=0){if(arr[cur])//如果说是非0{arr[dest--] = arr[cur--];}else//如果说是0{arr[dest--] = 0;arr[dest--] = 0;cur--;}}}
};

3.快乐数

题目链接：LINK

题解：

• 思路①：双指针算法
  • 详述：定义一个slow指针，每次算一次；定义一个fast指针，每次算两步，当slow == fast且是1时候则返回true；如果slow==fast且不是1，则返回false；
  • 时间复杂度：O(N)

class Solution {
public:int bitsum(int n){int sum = 0;while(n){sum+=(n%10)*(n%10);n/=10;}return sum;}bool isHappy(int n) {//1.定义两个指针int slow = bitsum(n);int fast = bitsum(bitsum(n));while(slow != fast){slow = bitsum(slow);fast = bitsum(bitsum(fast));}return slow == 1;}
};

4.盛最多水的容器

题目链接：LINK

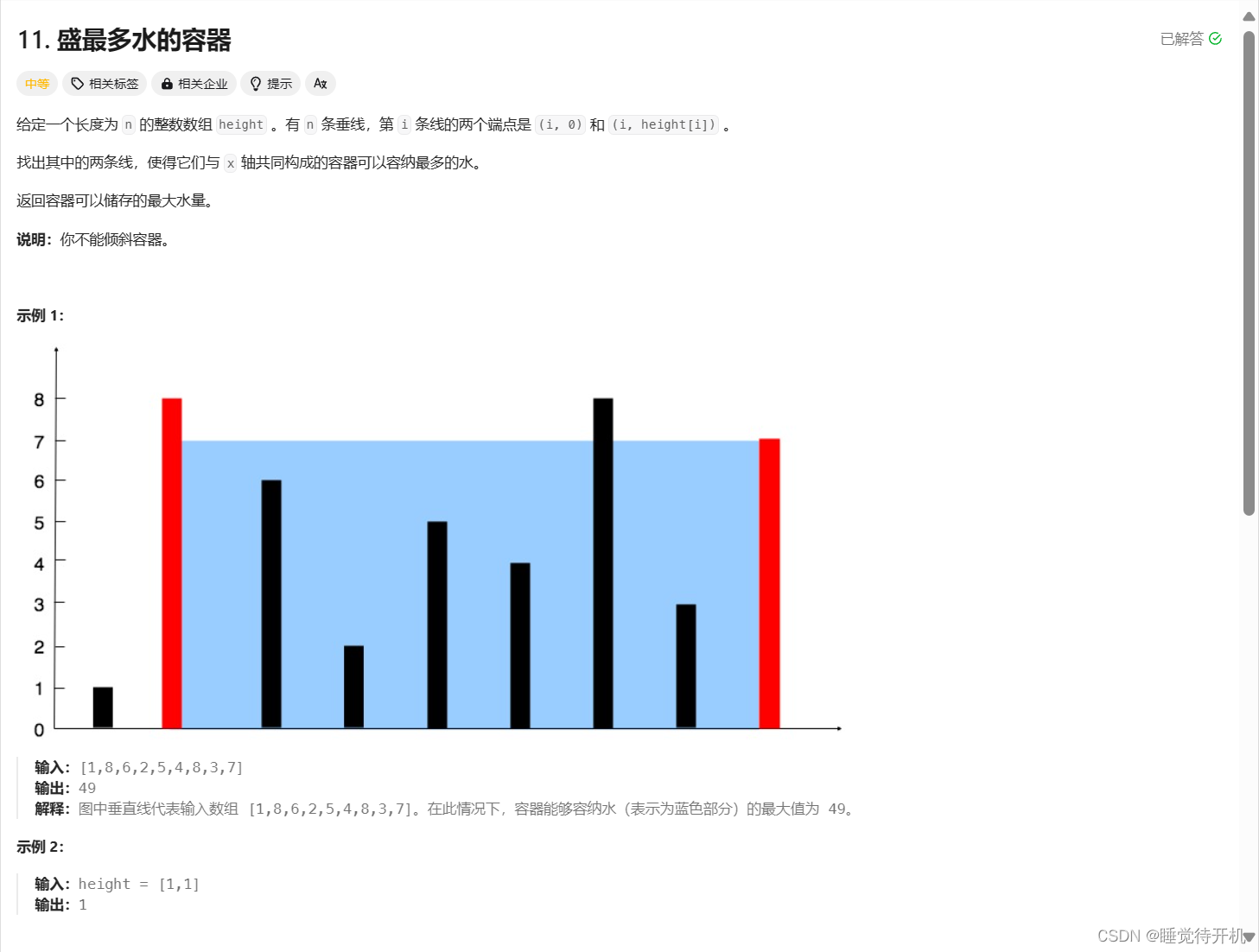
题解：

• 思路①：暴力求解
  • 详述：定义两个指针，依次枚举，取最大值
  • 时间复杂度：O(N^2)
• 思路②：双指针算法
  • 详述：定义两个指针，一个指向0下标处，另一个指向最后一个下标处，算出此时容器体积大小，然后如果left指针小，则left++，如果right小，则right–，依次类推，找出其中的最大值就好。
  • 时间复杂度：O(N)

class Solution {
public:int maxArea(vector<int>& height) {int first = 0,last = height.size()-1,ret = 0;while(first<last){ret = max(ret,(last - first) * min(height[first],height[last]));//移动指针if(height[first] < height[last]){first++;}else{last--;}}return ret;}
};

5.有效三角形的个数

题目链接：LINK

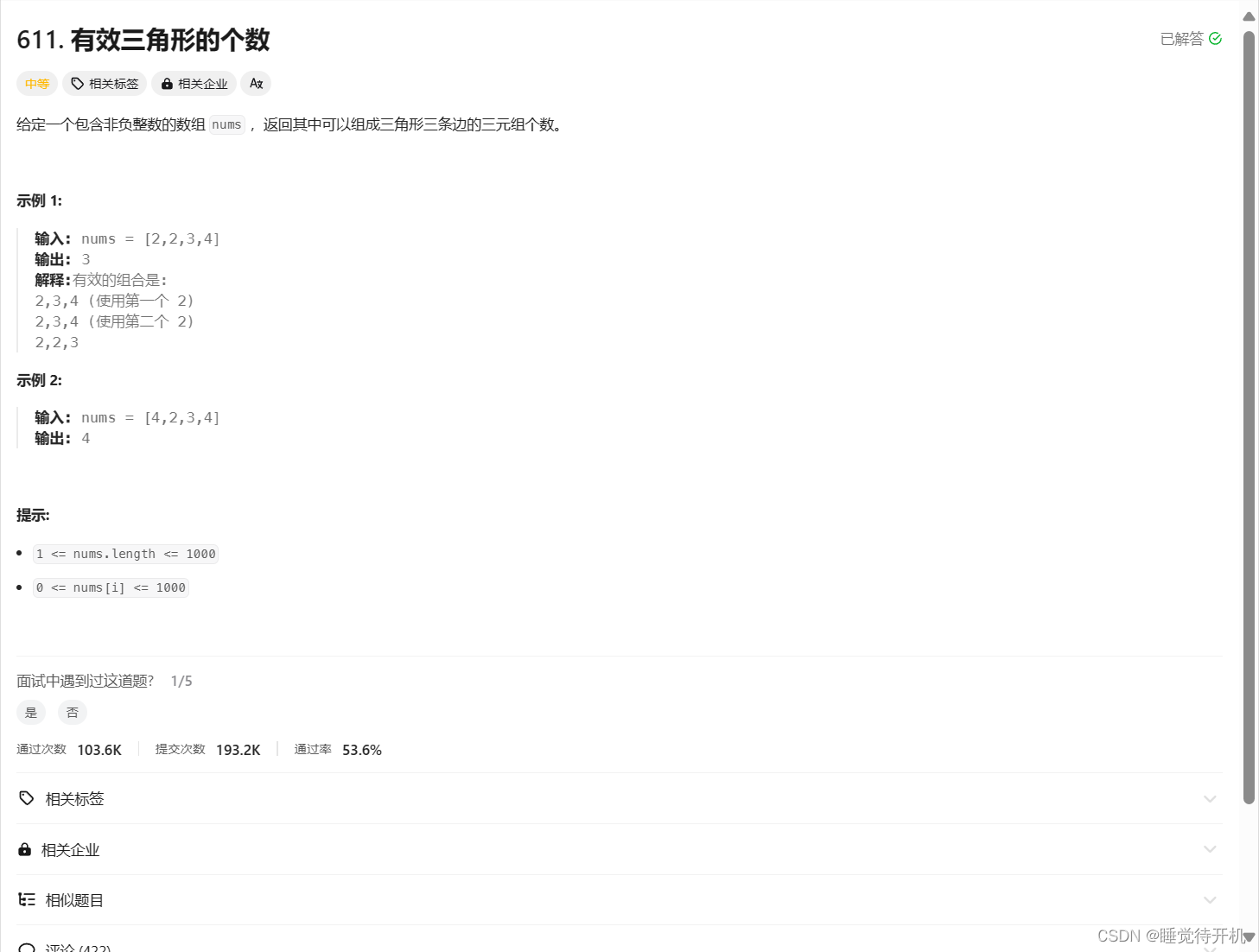
题解：

• 思路①：暴力求解
  • 详述：一次列举各种情况，进行求证即可。
  • 时间复杂度：O(N^3)
• 思路②：双指针算法
  • 详述：开始首先排序，再固定一个后面的大数，再定义两个指针，如果left+right处的值大于固定的数，那么就直接加上个数，如果小，就left++即可，以此类推。
  • 时间复杂度：O(N^2)

class Solution {
public:int triangleNumber(vector<int>& nums) {//先排序sort(nums.begin(),nums.end());//定义三个指针，一个用来固定位置，另外两个用来找int count = 0;for(int i = nums.size() - 1;i>=2;i--)//先固定一个数字{int left = 0;int right = i - 1;while(left < right){if(nums[left] + nums[right] > nums[i]){count += right - left;right--;}else{left++;}}}return count;}
};

6.和为s的两个数

题目链接：LINK

题解：

• 思路①：暴力求解
  • 详述：依次枚举，返回正确的数字
  • 时间复杂度：O(N^2)
• 思路②：双指针算法
  • 详述：left在最左端，right在最右端，sum太大，right–，sum太小，left++，sum==s，返回
  • 时间复杂度：O(N)

class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {//定义两个指针，大了调小，小了调大，等于返回int left = 0,right = price.size() - 1;while(left < right){if((price[left] + price[right]) < target){left ++;}else if((price[left] + price[right]) > target){right --;}else{return {price[left] , price[right]} ;   }}return {0,0};}
};

7.三数之和

题目链接：LINK

题解：

• 思路①：暴力求解
  • 详述：依次枚举，三重循环
  • 时间复杂度：O(N^3)
• 思路②：双指针算法
  • 详述：固定一个数a，left在左端，right在右端，看sum与-a的大小，若sum较大，right–，如果sum较小，那就left++…同时还应该注意去重问题。
  • 时间复杂度：O(N^2)

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> ret;//排序sort(nums.begin(),nums.end());//for(int i = 0;i<nums.size();)//先固定一个数{int left = i + 1,right = nums.size() - 1,target = -nums[i];if(target < 0){break;}while(left < right){int sum = nums[left] + nums[right];if(sum > target){right--;}else if(sum < target){left++;}else{ret.push_back({nums[i],nums[left],nums[right]});left++,right--;//去重while(left<right && nums[left] == nums[left-1]){left++;}while(right>left && nums[right] == nums[right+1]){right--;}}}i++;while(i < nums.size() && nums[i] == nums[i-1]){i++;}}return ret;}
};

8.四数之和

题目链接：LINK

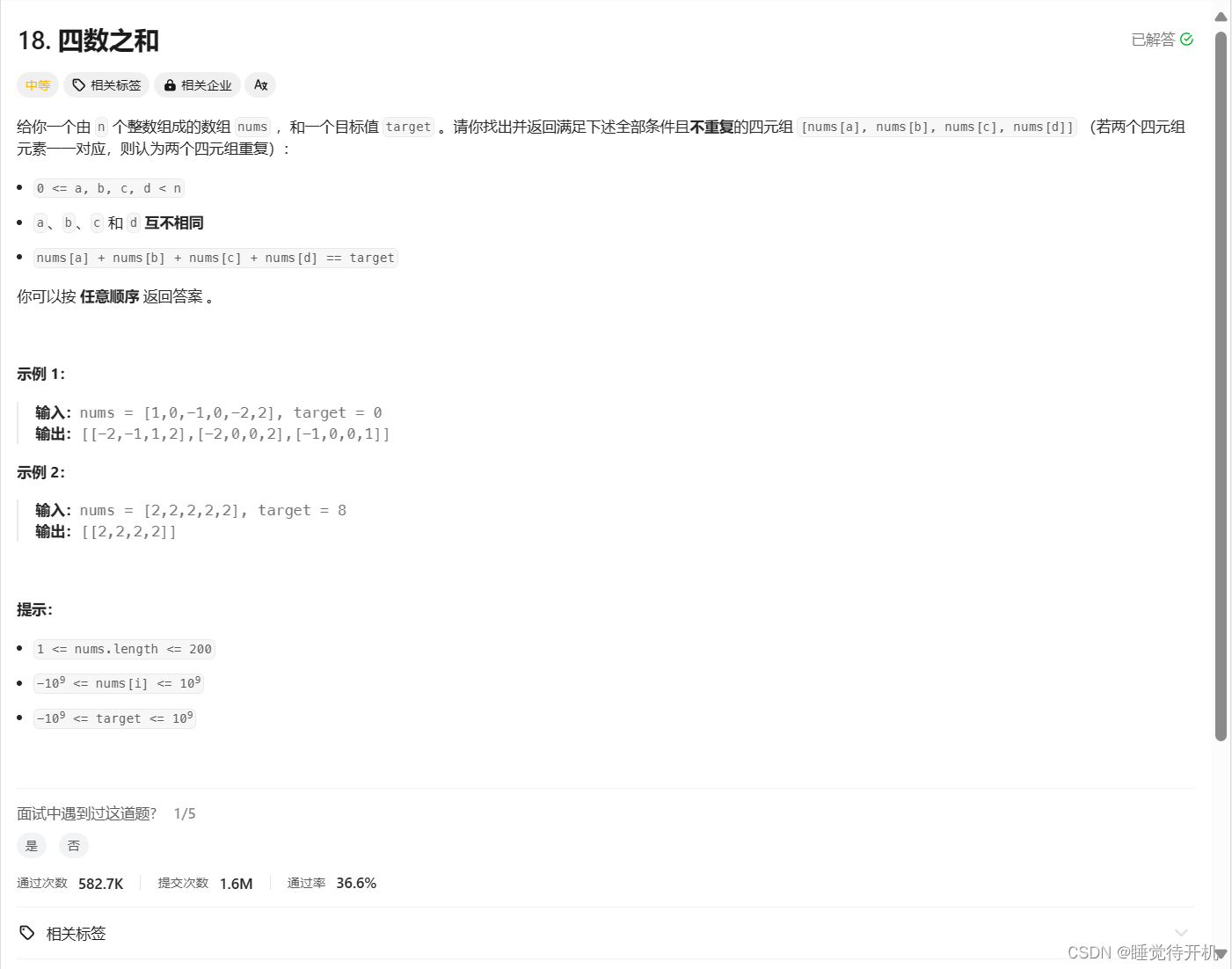
题解：

• 思路①：暴力求解
  • 详述：依次枚举，四层循环
  • 时间复杂度：O(N^4)
• 思路②：双指针算法
  • 详述：先固定一个数字，再借鉴”三数之和“的思路
  • 时间复杂度：O(N^3)

class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target){sort(nums.begin(), nums.end());vector<vector<int>> ret;int n = nums.size();for (int a = 0; a < n;)//固定数a{for (int b = a + 1; b < n;)//固定数b{int left = b + 1, right = n - 1;long long LFtarget = (long long)target - nums[a] - nums[b];while (left < right){int LFsum = nums[left] + nums[right];if (LFsum > LFtarget){right--;}else if (LFsum < LFtarget){left++;}else{ret.push_back({ nums[a],nums[b],nums[left],nums[right] });left++, right--;//去重 left and rightwhile (left < right && nums[left] == nums[left - 1]){left++;}while (left < right && nums[right] == nums[right + 1]){right--;}}//end else}//end left and right whileb++;while (b < n && nums[b] == nums[b - 1]){b++;}}//end b whilea++;while (a < n && nums[a] == nums[a - 1]){a++;}}// end a whilereturn ret;}
};

---

EOF