刚开始想着用最小堆，把每个元素都加进去，然后找出最小的k个值，复杂度应该是（n+klogn)

import heapq as pq
class Solution:def __init__(self):self.h = []pq.heapify(self.h)def closestKValues(self, root: Optional[TreeNode], target: float, k: int) -> List[int]:if not root: returnself.target = targetself.dfs(root)ans = []for i in range(k):ans.append(pq.heappop(self.h)[1])return ansdef dfs(self, root):if not root: returnpq.heappush(self.h, [abs(self.target - root.val), root.val])self.dfs(root.left)self.dfs(root.right)

题目要求在（n)的复杂度下解决。

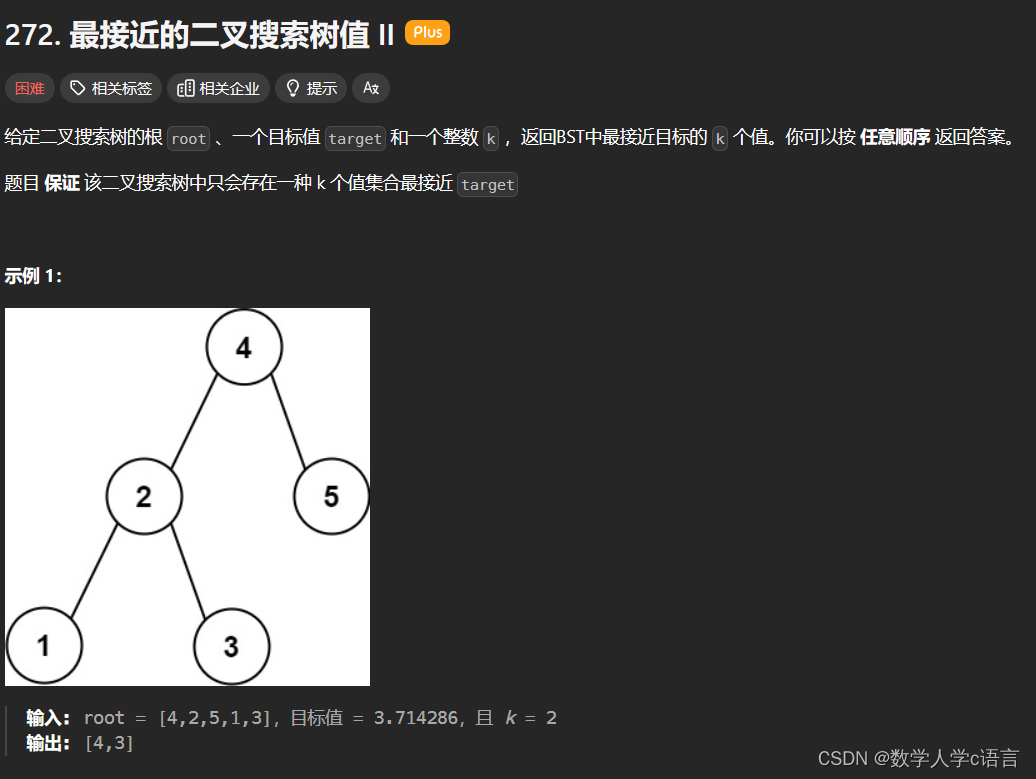
终于发现，题目给的是二叉搜索树，特点是：左子节点<当前节点<右子节点

那思路就来了：

1.把所有节点都放在列表ls中

2.找到第一个大于target的值

3.双指针，一个指针向左走，一个指针向右转，距离target最小的节点的值保留。

class Solution:def closestKValues(self, root: Optional[TreeNode], target: float, k: int) -> List[int]:if not root: returnself.ls = []self.dfs(root)leth = len(self.ls)l, r = 0, leth - 1while l < r:mid = l + r >> 1if self.ls[mid] < target:l = mid + 1else:r = midl, r = l-1, lans = []while k and l >= 0 and r < leth:n1 = abs(self.ls[l] - target)n2 = abs(self.ls[r] - target)if n1 <= n2:ans.append(self.ls[l])l -= 1else:ans.append(self.ls[r])r += 1k -= 1if k > 0:if l < 0: ans += self.ls[r:r+k]else: ans += self.ls[l-k+1:l+1]return ansdef dfs(self, root):if not root: returnself.dfs(root.left)self.ls.append(root.val)self.dfs(root.right)

复杂度为（n+logn+k），四舍五入满足题目的条件。