数据结构-AVL树

目录

什么是 AVL 树

ASL 度量查找效率

结构体定义

平衡调整

调整类型

左旋和右旋

右旋

左旋

左、右平衡调整

左平衡调整

右平衡调整

插入数据

模拟建立 AVL 树

什么是 AVL 树

        二叉排序树的形状取决于数据集，当二叉树的高度越小、结构越合理，搜索的性能就越好，时间复杂度 O(log2n)。G. M. Adelson-Velsky 和 E. M. Landis 在1962年的论文《An algorithm for the organization of information》中发表了一种名为 AVL 树的数据结构，它就能很好地解决这个问题。AVL 树具有以下 2 个性质：

  1. 左子树和右子树的深度之差的绝对值不超过 1；
  2. 左子树和右子树通通都是 AVL 树。

        其中为了度量左右子树的深度之差，我们引入平衡因子 (BF)"的概念。例如下面的二叉搜索树的平衡因子为：

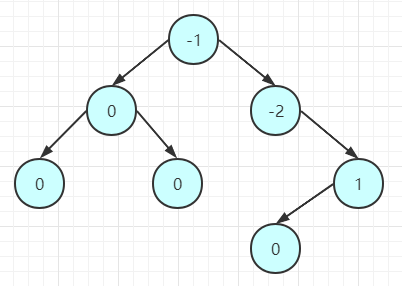
        对于一棵 AVL 树，里面的所有结点的平衡因子只能取值于：-1、0、1。

ASL 度量查找效率

        为了更好地理解 AVL 树，请认真观察下面 2 个二叉搜索树，我们发现第二个二叉搜索树是 AVL 树，树的高度更小，查找的比较次数也更少，效率更高。


        现在计算一下该 AVL 树的 ASL：

ASL(成功)：(1 + 2 × 2 + 3 × 4) ÷ 6 = 17/6
ASL(失败)：4 × 8 ÷ 8 = 4

        和二叉搜索树对比，发现无论是成功还是失败的 ASL，AVL 树的都较小，说明效率更高。

结构体定义

typedef struct BiTNode
{int data;int bf;  //平衡因子struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

平衡调整

调整类型

        由于二叉搜索树的结点是一个一个插入的，在插入时可能会造成结点的平衡因子的绝对值超过 1。造成失衡一共有 4 种情况：RR 型、LL 型、RL 型、LR 型，如图所示：

        虽然有 4 种情况，但是需要遵循的原则是一样的——在尽可能减小高度的前提下，保持二叉搜索树的性质。下面就看一下 4 种情况的调整示意图，不难发现都是遵循这个原则进行调整的。


        需要注意的是，当有多个结点失衡时，需要选择最小失衡子树来调整。

左旋和右旋

右旋

        右旋可以形象地理解为把最上面的结点掰下来，这种操作称之为“右旋”。右旋操作后指向新的根结点，即操作之前的根结点的左结点。

void R_Rotate(BiTree &T)
{ BiTree L;      //L 表示 T 的左子树L = T->lchild;    //L 指向 T 的左子树 T->lchild = L->rchild;      //T 的左子树更改为 T 的左子树的右子树  L->rchild = T;      //T 的左子树的右子树修改为 TT = ptr;      //根结点修改为右旋之前 T 的左子树
}

左旋

        对于 RR 型的调整，可以形象地理解为把最上面的结点掰下来，这种操作称之为“左旋”。左旋操作后指向新的根结点，即操作之前的根结点的右结点。

void L_Rotate(BiTree &T)
{ BiTree R;      //R 表示 T 的右子树R = T->rchild;        //R 指向 T 的右子树  T->rchild = R->lchild;      //T 的右子树更改为 T 的右子树的左子树  R->lchild = T;      //T 的右子树的左子树修改为 TT = R;      //根结点修改为左旋之前 T 的右子树
}

左、右平衡调整

左平衡调整

        这个函数为左平衡旋转，将 RL 型和 LL 型进行判断和操作。需要考虑涉及结点所连接的子树，对每个结点的 BF 都进行修正。

void LeftBalance(BiTree &T)
{ BiTree L;      //L 表示 T 的左子树BiTree Lr;      //Lr 表示 L 的右子树L = T->lchild;      //L 指向 T 的左结点 switch(L->bf)      //根据 T 的左子树的 BF 作相应平衡处理{case 1:          //LL 型，新结点插入在 T 的左结点的左子树{T->bf = L->bf = 0;      //修正 BF 均为 0R_Rotate(T);      //右旋操作break;}case -1:          //RL 型，新结点插入在 T 的左结点的右子树，要做双旋操作{Lr = L->rchild;       //Lr 指向示 L 的右结点switch(Lr->bf)      //修正 T 及其左结点的平衡因子{ case 1:            //Lr 平衡因子为 1{T->bf = -1;L->bf = 0;break;}case 0:            //Lr 平衡因子为 0{T->bf = L->bf = 0;break;}case -1:            //Lr 平衡因子为 -1{T->bf = 0;L->bf = 1;break;}}Lr->bf = 0;      //修正 Lr 平衡因子为 0L_Rotate(T->lchild);       //对 T 的左子树作左旋操作  R_Rotate(T);      //对 T 作右旋操作break;}}
}

右平衡调整

        这个函数为右平衡旋转，将 LR 型和 RR 型进行判断和操作。需要考虑涉及结点所连接的子树，对每个结点的 BF 都进行修正。

void RightBalance(BiTree &T)
{ BiTree R;      //R 表示 T 的右子树BiTree Rl;      //Rl 表示 R 的左子树R = T->rchild;      //R 指向 T 的右结点 switch(R->bf)      //根据 T 的右子树的 BF 作相应平衡处理{case -1:          //RR 型，新结点插入在 T 的右结点的右子树{T->bf = R->bf = 0;      //修正 BF 均为 0L_Rotate(T);      //左旋操作break;}case 1:          //LR 型，新结点插入在 T 的右结点的左子树，要做双旋操作{Rl = R->lchild;       //Rl 指向 R 的左结点switch(Rl->bf)      //修正 T 及其右结点的平衡因子{ case -1:            //Rl 平衡因子为 -1{T->bf = 1;R->bf = 0;break;}case 0:            //Rl 平衡因子为 0{T->bf = R->bf = 0;break;}case 1:            //Rl 平衡因子为 1{T->bf = 0;R->bf = -1;break;}}Rl->bf = 0;      //修正 Rl 平衡因子为 0R_Rotate(T->rchild);       //对 T 的右子树作右旋操作  L_Rotate(T);      //对 T 作左旋操作break;}}
}

插入数据

        要插入一个数据，首先需要判断这个数据是否已存在，若在 AVL 树中不存在要插入的数据，则执行插入操作。函数将通过递归找到合适的插入位置，如果在插入时出现失去平衡的情况，要进行对应的平衡旋转处理。

bool InsertAVL(BiTree &T, int e, bool &taller) {// taller 表示树的高度是否发生变化if (T == NULL) { // 若传入的 T 为空树，将创建根结点T = new BiTNode;T->data = e;T->bf = 0;T->lchild = T->rchild = NULL;taller = true; // 表示树的高度是否发生变化} else {if (e == T->data) { // 和 e 有相同数据的结点已存在taller = false;return false;}if (e < T->data) { // 进入左子树搜索插入位置if (InsertAVL(T->lchild, e, taller) == false) { // 结点已存在return false;}if (taller == true) { // 数据插入 T 的左子树中并且高度发生变化switch (T->bf) { // 检查 T 的 BF 判断是否调整case 1: // 原本左子树比右子树高，需要进行左平衡处理LeftBalance(T); // 左平衡处理taller = false;break;case 0: // 原本左、右子树等高，仍保持平衡，修正 BFT->bf = 1;taller = true;break;case -1: // 原本右子树比左子树高，仍保持平衡，修正 BFT->bf = 0;taller = false;break;}}} else { // 进入右子树搜索插入位置if (InsertAVL(T->rchild, e, taller) == false) { // 结点已存在return false;}if (taller == true) { // 数据插入 T 的左子树中并且高度发生变化switch (T->bf) { // 检查 T 的 BF 判断是否调整case 1: // 原本右子树比左子树高，仍保持平衡，修正 BFT->bf = 0;taller = false;break;case 0: // 原本左、右子树等高，仍保持平衡，修正 BFT->bf = -1;taller = true;break;case -1: // 原本右子树比左子树高，需要进行右平衡处理RightBalance(T);taller = false;break;}}}}return true;
}

模拟建立 AVL 树

        按照整数序列 {4,5,7,2,1,3,6} 依次插入的顺序构造相应平衡二叉树。
        首先结点 4 加入 AVL 树成为根结点。

        结点 5 加入 AVL 树。

        结点 7 加入 AVL 树，此时结点 4 的平衡因子为 -2，需要进行调整。


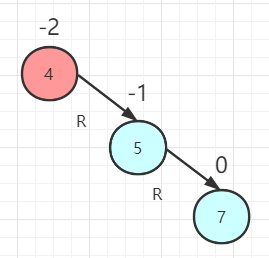
        进行 RR 型调整。

        结点 2 加入 AVL 树。

        结点 1 加入 AVL 树，此时结点 4 的平衡因子为 2，需要进行调整。

        进行 LL 型调整。

        结点 3 加入 AVL 树，此时结点 5 的平衡因子为 2，需要进行调整。

        进行 LR 型调整。

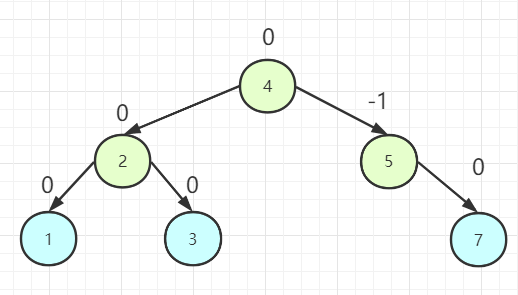
        结点 6 加入 AVL 树，此时结点 5 的平衡因子为 -2，需要进行调整。

        进行 RL 型调整。

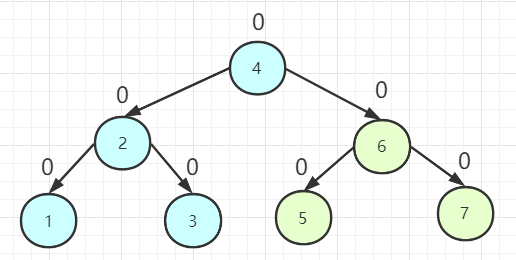
        到此为止，AVL 树建立完毕。完整的代码实现如下：

#include <stdio.h>
#include <stdlib.h>// AVL树的节点结构
typedef struct BiTNode {int data;int bf; // 平衡因子struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;// 右旋转
void R_Rotate(BiTree *P) {BiTree L;L = (*P)->lchild;(*P)->lchild = L->rchild;L->rchild = (*P);*P = L;
}// 左旋转
void L_Rotate(BiTree *P) {BiTree R;R = (*P)->rchild;(*P)->rchild = R->lchild;R->lchild = (*P);*P = R;
}// 左平衡旋转处理
void LeftBalance(BiTree *T) {BiTree L, Lr;L = (*T)->lchild;switch (L->bf) {case 1:(*T)->bf = L->bf = 0;R_Rotate(T);break;case -1:Lr = L->rchild;switch (Lr->bf) {case 1:(*T)->bf = -1;L->bf = 0;break;case 0:(*T)->bf = L->bf = 0;break;case -1:(*T)->bf = 0;L->bf = 1;break;}Lr->bf = 0;L_Rotate(&(*T)->lchild);R_Rotate(T);}
}// 右平衡旋转处理
void RightBalance(BiTree *T) {BiTree R, Rl;R = (*T)->rchild;switch (R->bf) {case -1:(*T)->bf = R->bf = 0;L_Rotate(T);break;case 1:Rl = R->lchild;switch (Rl->bf) {case 1:(*T)->bf = 0;R->bf = -1;break;case 0:(*T)->bf = R->bf = 0;break;case -1:(*T)->bf = 1;R->bf = 0;break;}Rl->bf = 0;R_Rotate(&(*T)->rchild);L_Rotate(T);}
}// 插入节点到AVL树中
int InsertAVL(BiTree *T, int key, int *taller) {if (!*T) {*T = (BiTree)malloc(sizeof(BiTNode));(*T)->data = key;(*T)->lchild = (*T)->rchild = NULL;(*T)->bf = 0;*taller = 1;} else {if (key == (*T)->data) { // 树中已存在相同的节点*taller = 0;return 0;}if (key < (*T)->data) { // 插入到左子树if (!InsertAVL(&((*T)->lchild), key, taller))return 0;if (*taller) { // 高度增加了switch ((*T)->bf) {case 1:LeftBalance(T);*taller = 0;break;case 0:(*T)->bf = 1;*taller = 1;break;case -1:(*T)->bf = 0;*taller = 0;break;}}} else { // 插入到右子树if (!InsertAVL(&((*T)->rchild), key, taller))return 0;if (*taller) { // 高度增加了switch ((*T)->bf) {case 1:(*T)->bf = 0;*taller = 0;break;case 0:(*T)->bf = -1;*taller = 1;break;case -1:RightBalance(T);*taller = 0;break;}}}}return 1;
}int main() {int count;      // 数据元素的个数BiTree T = NULL;int taller, flag; // taller 反映 T 的高度是否变化int a_num;      // 暂存输入数据scanf("%d", &count);for (int i = 0; i < count; i++) {scanf("%d", &a_num);flag = InsertAVL(&T, a_num, &taller); // 向 AVL 树中插入 a_num}return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/831400.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

thinkphp家政上门预约服务小程序家政保洁师傅上门服务小程序上门服务在线派单安装教程

thinkphp家政上门预约服务小程序家政保洁师傅上门服务小程序上门服务在线派单安装教程

介绍 thinkphp家政上门预约服务小程序家政保洁师傅上门服务小程序上门服务在线派单安装教程 上门预约服务派单小程序家政小程序同城预约开源代码独立版安装教程 程序完整&#xff0c;经过安装检测&#xff0c;可放心下载安装。 适合本地的一款上门预约服务小程序&#xff0…
阅读更多...
计算机网络——初识网络

计算机网络——初识网络

一、局域网与广域网 1.局域网&#xff08;LAN&#xff09; 局域网&#xff1a;即Local Area Network&#xff0c;简称LAN。Local即标识了局域⽹是本地&#xff0c;局部组建的⼀种私有⽹络。局域⽹内的主机之间能⽅便的进⾏⽹络通信&#xff0c;⼜称为内⽹&#xff1b;局域⽹和…
阅读更多...
A4的PDF按A3打印

A4的PDF按A3打印

先用办公软件打开&#xff0c;比如WPS。 选择打印-属性。 纸张选A3&#xff0c;如果是双面打印&#xff0c;选短边装订&#xff0c;然后在版面-页面排版-每张页数&#xff08;N合1&#xff09;选2。 不同打印机的具体配置可能不一样&#xff0c;但大体都是这个套路。
阅读更多...
[NSSCTF]prize_p1

[NSSCTF]prize_p1

前言 之前做了p5 才知道还有p1到p4 遂来做一下 顺便复习一下反序列化 prize_p1 <META http-equiv"Content-Type" content"text/html; charsetutf-8" /><?phphighlight_file(__FILE__);class getflag{function __destruct(){echo getenv(&qu…
阅读更多...
The Role of Subgroup Separability in Group-Fair Medical Image Classification

The Role of Subgroup Separability in Group-Fair Medical Image Classification

文章目录 The Role of Subgroup Separability in Group-Fair Medical Image Classification摘要方法实验结果 The Role of Subgroup Separability in Group-Fair Medical Image Classification 摘要 研究人员调查了深度分类器在性能上的差异。他们发现&#xff0c;分类器将个…
阅读更多...
基于Springboot的民宿管理平台

基于Springboot的民宿管理平台

基于SpringbootVue的民宿管理平台设计与实现 开发语言&#xff1a;Java数据库&#xff1a;MySQL技术&#xff1a;SpringbootMybatis工具&#xff1a;IDEA、Maven、Navicat 系统展示 用户登录 首页 民宿信息 后台登录 后台首页 用户管理 商家管理 民宿信息管理 房间类型管理 …
阅读更多...
【正版系统】知识付费系统搭建，系统模板开发完善功能强大，支持快速部署上线

【正版系统】知识付费系统搭建，系统模板开发完善功能强大，支持快速部署上线

在数字化时代&#xff0c;知识付费已成为一种趋势&#xff0c;为内容创作者和求知者搭建了一个高效的交流平台。今天&#xff0c;我要为大家介绍一款功能强大的知识付费系统。 知识付费系统模板是我们一款经过精心开发、完善的系统&#xff0c;旨在为用户提供一站式的知识付费…
阅读更多...
【Docker】如何注册Hub账号并上传镜像到Hub仓库

【Docker】如何注册Hub账号并上传镜像到Hub仓库

一、创建Hub账户 浏览器访问&#xff1a;hub.docker.com 点击【Sign up】注册账号 输入【邮箱】【用户名】【密码】 ps&#xff1a;用户名要有字母数字&#xff1b;订阅不用勾选 点击【Sign up】注册即可 点击【Sign in】登录账号 输入【邮箱】【密码】 点击【Continue】登录 二…
阅读更多...
Unreal 编辑器工具 批量重命名资源

Unreal 编辑器工具 批量重命名资源

右键 - Editor Utilities - Editor Utility Blueprint&#xff0c;基类选择 Asset Action Utility 在类默认值内&#xff0c;可以添加筛选器&#xff0c;筛选指定的类型 然后新建一个函数&#xff0c;加上4个输入&#xff1a;ReplaceFrom&#xff0c;ReplaceTo&#xff0c;Add…
阅读更多...
大数据学习笔记14-Hive基础2

大数据学习笔记14-Hive基础2

一、数据字段类型 数据类型 &#xff1a;LanguageManual Types - Apache Hive - Apache Software Foundation 基本数据类型 数值相关类型 整数 tinyint smallint int bigint 小数 float double decimal 精度最高 日期类型 date 日期 timestamps 日期时间 字符串类型 s…
阅读更多...
nginx--自定义日志跳转长连接文件缓存状态页

nginx--自定义日志跳转长连接文件缓存状态页

自定义日志服务 [rootlocalhost ~]# cat /apps/nginx/conf/conf.d/pc.conf server {listen 80;server_name www.fxq.com;error_log /data/nginx/logs/fxq-error.log info;access_log /data/nginx/logs/fxq-access.log main;location / {root /data/nginx/html/pc;index index…
阅读更多...
使用STM32F103C8T6与蓝牙模块HC-05连接实现手机蓝牙控制LED灯

使用STM32F103C8T6与蓝牙模块HC-05连接实现手机蓝牙控制LED灯

导言： 在现代智能家居系统中，远程控制设备变得越来越普遍和重要。本文将介绍如何利用STM32F103C8T6单片机和蓝牙模块HC-05实现远程控制LED灯的功能。通过这个简单的项目，可以学会如何将嵌入式系统与蓝牙通信技术相结合，实现远程控制的应用。 目录 导言： 准备工作： 硬…
阅读更多...
Java零基础入门到精通_Day 11

Java零基础入门到精通_Day 11

1.继承 定义&#xff1a; 继承是面向对象三大特征之一。可以使得子类具有父类的属性和方法&#xff0c;还可以在子类中重新定义&#xff0c;追加属性和方法 格式&#xff1a; public class 子类 extends 父类{} 子类&#xff1a;也叫派生类 父类&#xff1a;基类/超类 继…
阅读更多...
低代码技术在构建质量管理系统中的应用与优势

低代码技术在构建质量管理系统中的应用与优势

引言 在当今快节奏的商业环境中&#xff0c;高效的质量管理系统对于组织的成功至关重要。质量管理系统帮助组织确保产品或服务符合客户的期望、符合法规标准&#xff0c;并持续改进以满足不断变化的需求。与此同时&#xff0c;随着技术的不断进步&#xff0c;低代码技术作为一…
阅读更多...
机器学习笔记-14

机器学习笔记-14

机器学习系统设计 1.导入 以垃圾邮件分类器为例子&#xff0c;当我们想要做一个能够区分邮件是否为垃圾邮件的项目的时候&#xff0c;首先在大量垃圾邮件中选出出现频次较高的10000-50000词作为词汇表&#xff0c;并为其设置特征&#xff0c;在对邮件分析的时候输出该邮件的特…
阅读更多...
计算机网络-408考研

计算机网络-408考研

后续更新发布在B站账号&#xff1a;谭同学很nice http://【计算机408备考-什么是计算机网络&#xff0c;有什么特点&#xff1f;】 https://www.bilibili.com/video/BV1qZ421J7As/?share_sourcecopy_web&vd_source58c2a80f8de74ae56281305624c60b13http://【计算机408备考…
阅读更多...
在idea中连接mysql

在idea中连接mysql

IDE&#xff08;集成开发环境&#xff09;是一种软件应用程序&#xff0c;它为开发者提供编程语言的开发环境&#xff0c;通常集成了编码、编译、调试和运行程序的多种功能。一个好的IDE可以大幅提高开发效率&#xff0c;尤其是在进行大型项目开发时。IDE通常包括以下几个核心组…
阅读更多...
Docker-Compose编排lnmp(dockerfile) 完成Wordpress

Docker-Compose编排lnmp(dockerfile) 完成Wordpress

目录 一、创建nginx镜像 二、创建mysql镜像 三、创建php镜像 四、启动wordpress 五、安装Compose 六、准备环境 ​编辑 七、编写docker-compose.yml 八、启动并运行 九、浏览器访问 一、创建nginx镜像 #基于基础镜像 FROM centos:7 #用户信息 MAINTAINER this is ngi…
阅读更多...
LabVIEW换智能仿真三相电能表研制

LabVIEW换智能仿真三相电能表研制

LabVIEW换智能仿真三相电能表研制 在当前电力工业飞速发展的背景下&#xff0c;确保电能计量的准确性与公正性变得尤为重要。本文提出了一种基于LabVIEW和单片机技术&#xff0c;具有灵活状态切换功能的智能仿真三相电能表&#xff0c;旨在通过技术创新提高电能计量人员的培训…
阅读更多...
vue初始化项目

vue初始化项目

打开终端输入vue create project-name 选择Manually select features回车&#xff0c;继续选择如下&#xff1a; 如果要使用pina就可以不选vuex&#xff0c;回车&#xff0c;选择如下&#xff1a; 按下图选即可
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023