深圳杯A题论文+代码分享资料链接:链接:https://pan.baidu.com/s/1L2NVgoefSW-yuqZjEB3wcw
提取码:sxjm
基于优化模型的多个火箭残骸的准确定位
摘要
在现代航天技术中,火箭是实现空间探索的关键工具。由于火箭发射过程中的高成本和复杂性,对火箭残骸的回收与重用变得越来越重要。本文将基于题目给出数据构建优化模型对火箭残骸进行准确定位。
问题一,单个残骸音爆定位分析。首先需要将设备的地理坐标(经度、纬度)转换为一个更适合计算的坐标系统,残骸发生音爆的位置(x,y,z) 和时间t,使用多边测量技术建立方程组。为了提高计算精度构建一个优化模型进行求解,以预测时间和实际时间差的平方和为目标函数。应用 BFGS 方法进行最小化,找到最小化 objective_function 的变量值,这些值代表了音爆源的最佳估计位置和时间。
问题二、三,多残骸音爆的监测和定位,确定每个监测设备接收到的不同音爆数据属于哪个具体的残骸。涉及到了最优值的求解,属于优化模型。建立一个数学模型来解决多源定位问题。设置一个优化问题,以确定该残骸的位置和音爆时间。目标是最小化预测的音爆抵达时间和实际记录时间之间的误差。以时间差约束、速度约束、高度约束、声速随高度变化、考虑风速和风向的影响作为约束条件,使用非线性最优化方法差分进化进行求解。通过三维可视化验证了模型的有效性,并展示了监测设备和残骸的空间分布。
问题四,误差修正和精准定位,考虑到设备记录时间可能存在高达0.5秒的随机误差。首先,为每个设备记录的时间添加一个随机误差,模拟实际条件中可能的测量不准确性。这个误差可以通过添加一个均值为0,标准差为0.5秒的高斯(正态)噪声来模拟。优化目标函数为计算了预测的音爆抵达时间和观测时间之间的加权平方差之和。模型生成的结果通过三维可视化和时间分析进行了展示和验证,表明模型能够在存在随机测量误差时有效地估计残骸位置。
整体而言,通过建立数学模型并利用差分进化算法的全局优化能力,解决了复杂的火箭残骸定位问题,即便在存在测量误差的挑战下也能给出准确的位置估计。这为类似问题提供了一个强大的求解框架和验证方法。
关键词优化模型,火箭残骸准确定位,坐标转化,模型修正

23页论文 1万字+ 十页无水印照片


一、模型的建立与求解
5.1 问题一模型的建立与求解
5.1.1 数据分析
为了更加直观地展示原始位置,利用python以及题目给出的数据,绘制了可视化如下所示
表1问题一给出数据
| 设备 | 经度(°) | 纬度(°) | 高程(m) | 音爆抵达时间(s) |
| A | 110.241 | 27.204 | 824 | 100.767 |
| B | 110.780 | 27.456 | 727 | 112.220 |
| C | 110.712 | 27.785 | 742 | 188.020 |
| D | 110.251 | 27.825 | 850 | 258.985 |
| E | 110.524 | 27.617 | 786 | 118.443 |
| F | 110.467 | 27.921 | 678 | 266.871 |
| G | 110.047 | 27.121 | 575 | 163.024 |

图1可视化结果
在这个坐标系中,设备A位于图中较高的位置,而设备G位于相对较低的位置。这种布局说明设备被布置在具有不同高度的地形上。通过这种三维分布,设备能够探测和追踪从不同高度和方向传来的音爆信号。
这张图也展示了设备之间的相对距离,这对于后续的分析很重要,比如利用声波到达的时间差来定位音爆发生的位置。再利用音爆抵达时间增加了声波传播球体的三维可视化,它展示了以七个监测设备为圆心,音爆抵达时间转换为半径(考虑声速)的球体。如下所示

图2可视化结果
每个球体用不同的颜色表示,以区分它们是从哪个设备中心展开的,与设备的颜色标记相对应。这些彩色的透明球体在三维空间中相互重叠。
l 监测设备位置图中显示了每个监测设备的位置,用大小相等且颜色不同的点表示,每个点的具体位置都标记在了对应的坐标上。
l 声波传播球体每个设备的声波传播球体通过一个半透明的网状结构表示,球体的大小(半径)与音爆抵达各设备的时间成比例。球体的交点是关键区域,因为这些区域表示了可能的音爆源位置。
l 球体交叉在图中,可以看到这些球体在某些区域相交。这些交点(或交叉区域)有助于确定音爆的原始位置。理论上,所有球体的交点将形成一个或多个共同的交集区域,即是音爆的发生位置。
l 三维空间理解在三维空间中,Z轴的伸展有助于了解球体高程方面的差异。球体的覆盖层和重叠区域的大小和形状提供了音爆源位置可能的高度信息。
5.1.2 单个残骸定位的建立
首先需要将设备的地理坐标(经度、纬度)转换为一个更适合计算的坐标系统,如笛卡尔坐标系。可以使用下列近似方法
将纬度转换为Y坐标=纬度×111263Y=纬度×111263米(纬度每度的距离)
将经度转换为X坐标=经度×97304X=经度×97304米(经度每度的距离,取决于纬度)
高程(Z坐标)直接使用给定的米值
最终具体的转化结果为表1转化结果
| 设备 | X (米) | Y (米) | Z (米) | 时间 (秒) |
| A | 10,726,890.26 | 3,026,798.65 | 824 | 100.767 |
| B | 10,779,337.12 | 3,054,836.93 | 727 | 112.22 |
| C | 10,772,720.45 | 3,091,442.46 | 742 | 188.02 |
| D | 10,727,863.30 | 3,095,892.98 | 850 | 258.985 |
残骸发生音爆的位置(x,y,z) 和时间t。给定7台设备的三维坐标和音爆抵达时间,可以使用多边测量技术建立以下方程组,对于每个设备i:
![]()
这里,(xi,yi,zi)和ti分别是第i台设备的坐标和音爆抵达时间。需要解这个方程组来找出(x,y,z,t)。
对于四个变量的方程组求解,最少需要四个方程,即至少需要布置四台监测设备,即可完成后续验证。这里题目给出了七台监测设备,因此,构建一个优化模型进行求解,以预测时间和实际时间差的平方和为目标函数,定义了一个 objective_function,该函数接受四个变量(x, y, z 位置坐标和音爆发生的时间 t),计算了预测的音爆抵达各个设备的时间,并将其与实际抵达时间进行比较。应用 BFGS 方法进行最小化,找到最小化 objective_function 的变量值,这些值代表了音爆源的最佳估计位置和时间。
具体模型如下所示
目标函数

其中,
l v 是包含x,y,z,t 的向量。
l t 是音爆发生时间。
l (x,y,z) 是音爆发生的位置。
l c 是声速。
l (xi,yi,zi,ti) 是第 i 个设备的坐标和音爆抵达时间。
l n 是设备数量。
目标是最小化f(v),即预测时间和实际时间的平方差的和。
5.1.3 单个残骸定位的求解
最小化过程


5.2 问题二三模型的建立与求解
5.2.1 数据分析
声波从音爆源到监测设备的传播是一个球面波,其半径随时间增加而扩大。对于每个残骸,它在空中发生音爆时会产生一个扩散的声波球。与问题一给出数据相同,为了更加直观的展示给出数据,首先以A为例绘制了二维平面、三维平面的声波球。
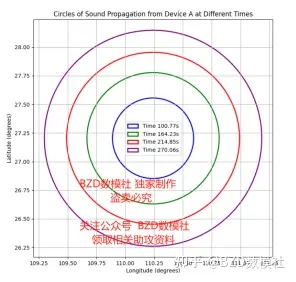


)


)




:抽象工厂模式)




 是非对错)

)

