一、树的先根遍历：

先根遍历：若树非空，先访问根结点，再依次对每棵子树进行先根遍历。

 

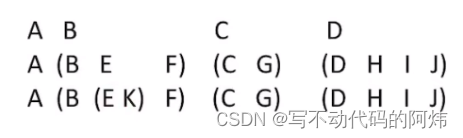
//树的先根遍历
void Pre0rder(TreeNode *R){if(R!=NULL){visit(R);               //访问根节点while(R还有下一个子树T)Pre0rder(T);         //先根遍历下一棵子树}
}

 转化成对应二叉树：

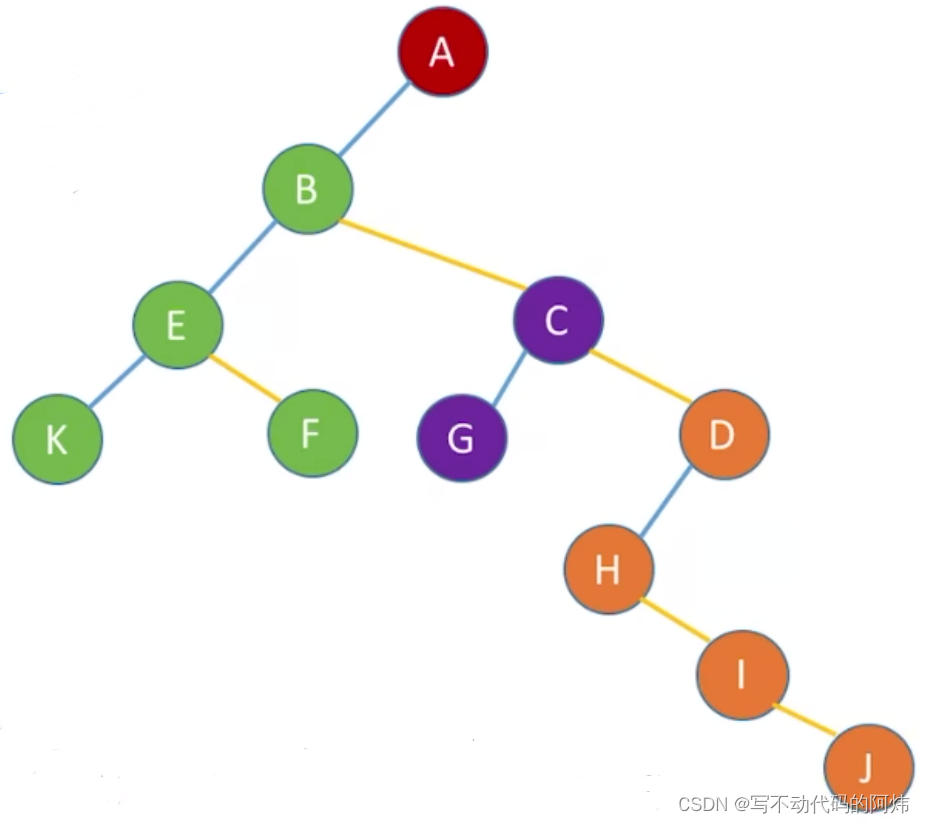
 树的先根遍历序列与这棵树相应二叉树的先序序列相同。

二、树的后根遍历：

后根遍历：若树非空，先依次对每棵子树进行后根遍历，最后再访问根结点。

 

//树的后根遍历
void Post0rder(TreeNode *R){if (R!=NULL){while(R还有下一个子树T)Post0rder(T);      //后根遍历下一棵子树visit(R); //访问根节点}
}

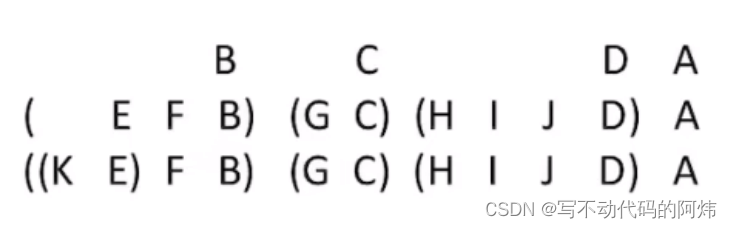
 转化成二叉树：

 树的后根遍历序列与这棵树相应二叉树的中序序列相同。

tips：先根和后跟遍历又称为深度优先遍历

  

三、树的层次遍历：

层次遍历（用队列实现)
①若树非空，则根节点入队
②若队列非空，队头元素出队并访问，同时将该元素的孩子依次入队
③重复②直到队列为空
tips:层次遍历又称为广度优先遍历。

四、森林的先序遍历：

森林。森林是m (m>0）棵互不相交的树的集合。每棵树去掉根节点后，其各个子树又组
成森林。

若森林为非空，则按如下规则进行遍历:访问森林中第一棵树的根结点。
先序遍历第一棵树中根结点的子树森林。
先序遍历除去第一棵树之后剩余的树构成的森林。

       

 

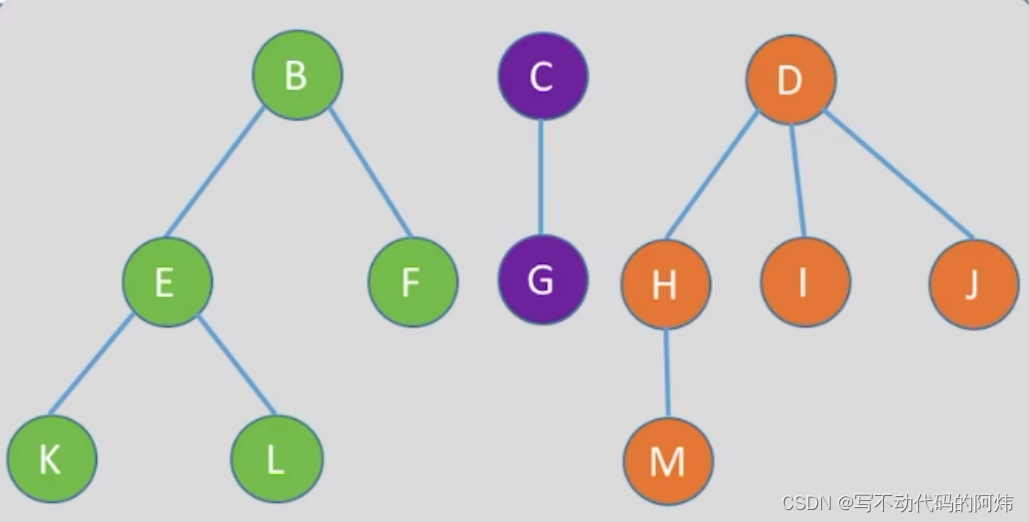
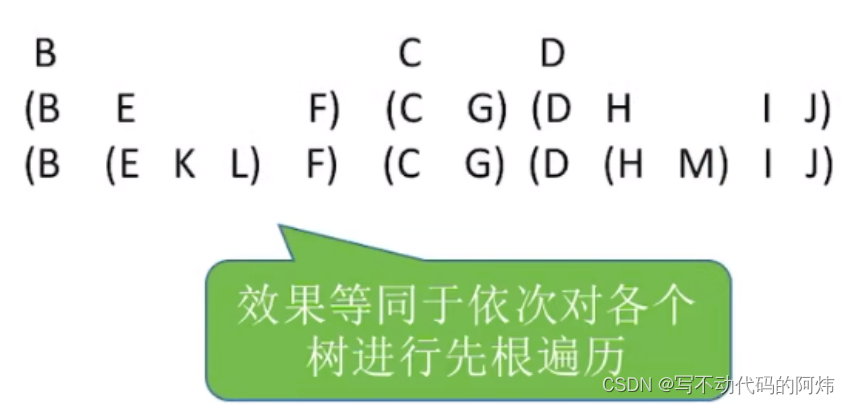
也可以把森林转化成相对应的二叉树：

                                     

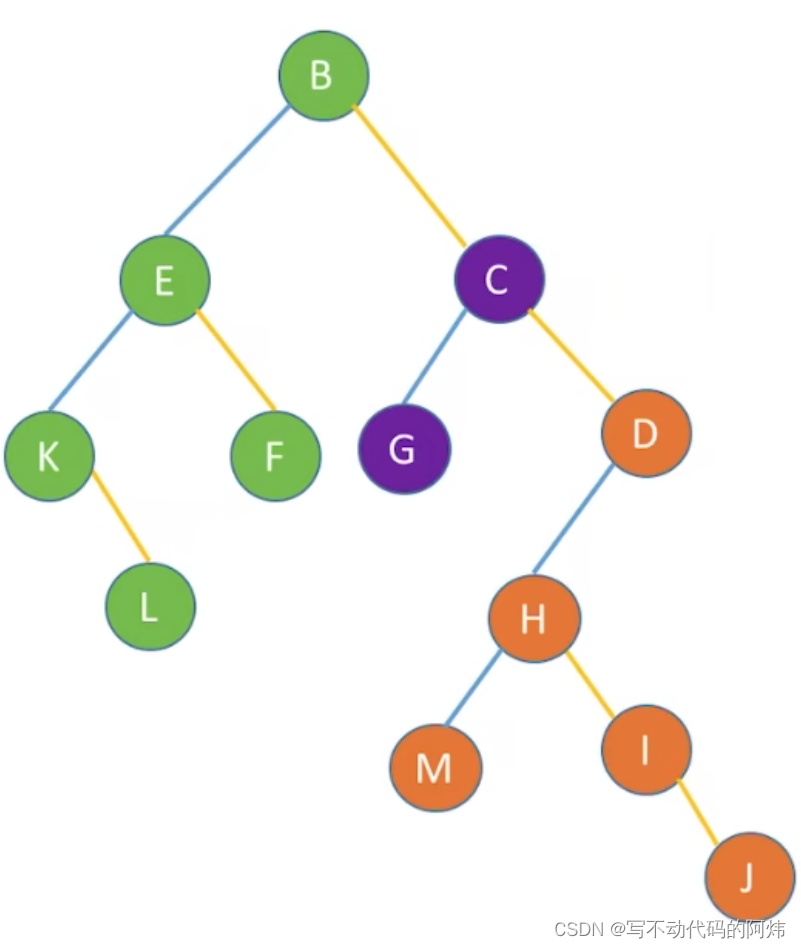
效果等同于依次对二叉树的先序遍历 

 

五、森林的中序遍历：

若森林为非空，则按如下规则进行遍历:
中序遍历森林中第一棵树的根结点的子树森林。访问第一棵树的根结点。
中序遍历除去第一棵树之后剩余的树构成的森林。

     

 

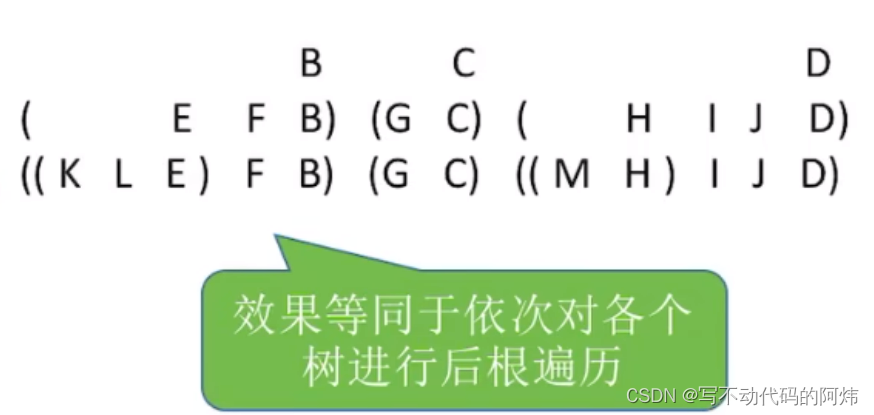
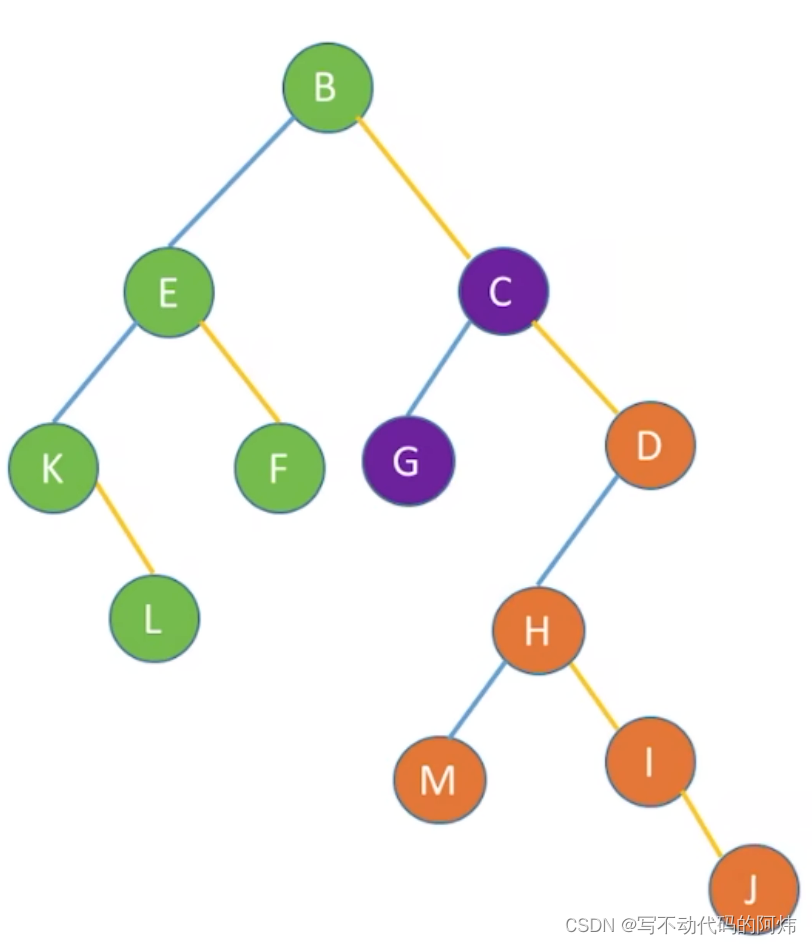
 也可以把森林转化成相对应的二叉树：