基于Matlab机器人工具箱对Dobot机械臂的研究

文章目录

前言

一、Dobot Mangician 分析

二、Matlab 机器人工具箱

1. 建立模型

2. DoBot 正向运动学

3. Dobot 逆运动学

4. Dobot workpace

5. Dobot轨迹规划

三、Dobot studio

1. DoBot teaching

2. DoBot Python 程序

总结

前言

在本实验中，以 Dobot Mangician 四自由度机械臂为例。实验研究了机器人的运动学和轨迹规划问题。为了实现对 Dobot 机械臂的运动学控制，采用了 Denavit-Hartenberg (D-H)建模方法来建立 Dobot 机械臂的运动学模型。其运动学正解和逆解是利用机械臂的奇偶变换矩阵获得的矩阵得到运动学正解和反解；并使用机器人工具箱对 Dobot 机械臂进行轨迹规划仿真。使用机器人工具箱对 Dobot 机械臂进行轨迹规划仿真。在本实验中，将使用 Matlab 和Dobot Mangician功能。

一、Dobot Mangician 分析

Dobot Magicician 由底座、大臂、小臂和末端执行器组成。如果 Dobot Magicician 没有安装末端工具，则包含三个关节: J1、J2 和 J3 都是旋转接头。如果 Dobot 魔术师安装了末端工具，如抓取器或吸盘工具，则包含四个关节： J1、J2、J3 和 J4 也都是旋转接头。第一自由度的角度范围为-90至90度，第二自由度的角度范围为0至85度，第三自由度的角度范围为-10至95度，第四自由度的角度范围为-90至90度。如图 (1) 和 (2) 所示（图片来自 dobot 网站：https://dobot.cn/products/education /magician.html)

二、Matlab 机器人工具箱

1. 建立模型

DobotMagician 机械臂有四个旋转关节，其中末端执行器是受机械约束的被动关节。机器人机械臂的坐标系是根据 D-H 参数和建立坐标系的规则建立的，因为机器人的第一自由度是距底座最低点 138 毫米，所以 d1 是 138。为了便于数据计算，对单位进行了统一定义，D-H 参数列于表中：

theta	d	a	alpha
L1 = Link([0	1.38	0	pi/2]);
L2 = Link([0	0	1.35	0]);
L3 = Link([0	0	1.47	pi/2]);
L4 = Link([0	0	0	0]);

使用 Matlab 环境下机器人工具箱中的 "Link "和 "robot "函数确定机器人在零位的姿态。然后根据 D-H 参数对机械臂进行建模，并使用 "qlim "函数设置每个关节的角度范围。然后使用 "SerialLink "函数依次连接三个关节。最后调用 "teach "函数控制 Dobot 模型，调整四个关节变量，实时控制机械臂的位置运动。Dobot 三维模型如图所示：

2. DoBot 正向运动学

前向运动学求解基于 Dobot 机械臂各关节的已知值，然后使用同质变换矩阵方程求解末端在空间中的位置。采用两种方法求解前向运动学：通过同质变换矩阵和使用机器人工具箱函数。

第一种方法是通过同质变换矩阵求解。首先给定每个关节的角度，然后利用坐标系 {i} 的关节相对于坐标系 {i-1} 的同质变换矩阵的一般方程，可以得到 Dobot 机器人手臂关节的变换矩阵如下：以 T1 为例：（详细代码参见附录）

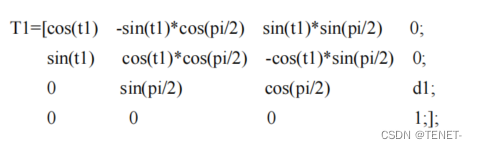
最后将每个链路的同质变换矩阵相乘，得到末端位置矩阵。

第二种方法是使用机器人工具箱来求解，这需要在建立模型后使用 fkine 函数，从而求出末端位置矩阵。找到末端位置矩阵。代码为 "dobot.fkine([0 , pi/7.554 ,-pi/4, 0])"。

3. Dobot 逆运动学

逆运动学的求解采用了同样的两种方法。逆运动学求解涉及根据机械臂末端的位置和姿态找到机械臂的关节角度，已知机械臂末端的位置会发生变化，但姿态始终垂直向下。位置矩阵是利用正解函数导出的位置矩阵来选择的。

第一种方法是在给出末端位置后，使用 "atan2() "函数求出 x 轴正方向与 xy 平面上的点 (x,y) 之间的夹角 "θ"。然后使用函数 "sqrt() "计算 Dobot 两节之间的夹角正弦。然后计算末端执行器的位置值，最后使用 "athan2() "函数计算第二自由度角。

第二种方法是使用机器人工具箱的函数进行求解。代码为 "q0=dobot.ikine(T0,'mask',[1 1 1 0 0 1])*180/pi"，代码末尾添加 180/pi 是为了使计算结果更加精确。

通过比较求解结果可以看出，正向运动学的结果与逆向运动学中定义的参数相同，而逆向运动学的结果与正向运动学中定义的角度相同。如图所示。

4. Dobot workpace

机械臂工作空间是机器人末端执行器可到达的所有位置空间点的集合。它可以用来衡量机器人的工作能力，也是存在正向运动学解决方案的区域。为确保 Dobot 机械臂工作时末端执行器始终处于工作空间内，应将 Dobot 的工作空间作为参考进行分析。根据蒙特卡洛法的 Dobot 工作空间求解思路，在关节角度变量范围内随机生成若干组每个关节角度。然后对每组角度分别进行正运动学求解，最终求解集即为工作空间。在本实验中，共生成了 3000 组随机数据，并将其输入正向运动学求解函数以找到工作空间。如图所示：

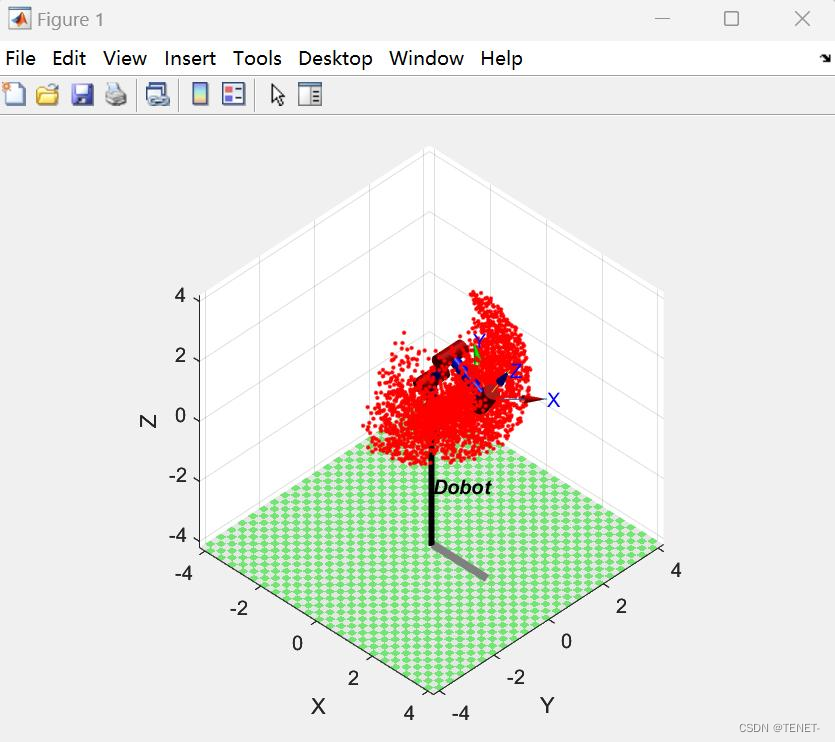
5. Dobot轨迹规划

轨迹规划可以避免实验过程中机械臂的损坏，为后续实验研究工作提供支持。在定义了多臂机器人的模型和参数后，使用 "flat "函数定义了五个点，这五个点分别是（2,0,2.38）；（2.5, 1, 1. 13）；（2,- 1.5,2.38）；（2,-1.5, 1. 13）；（2.6,0, 1.38）。然后使用 "ctraj "函数相互连接。然后使用 "transl "函数查找变换矩阵中的位置值，并使用 "mstraj "函数合并所有轨迹。然后使用 "axis "函数定义三维空间的大小。最后，使用逆运动学函数将轨迹点转换为多臂机关节角度，以便多臂机根据关节角度移动。根据关节角度移动。如图所示：

在代码中，还包括求解速度、加速度和位置的函数，当轨迹规划完成后，将在另一张图中显示，结果显示多臂机器人可以在这五个点之间移动。

三、Dobot studio

1. DoBot teaching

Dobot 教学模式可实现点对点运动。Dobot Magicician 的教学模式包括 MOVJ、MOVL 和 JUMP。不同的运动模式在教学后会有不同的运动轨迹。

MOVJ：关节运动，从 A 点到 B 点。每个关节从 A 点对应的关节角度运动到 B 点对应的关节角度，同时到达终点。

MOVL：直线运动，A 点到 B 点的直线运动。
JUMP ：门轨迹，A 点到 B 点以 MOVJ 运动模式运动，在 MOVJ 运动模式下上升到一定高度，在 MOVJ 运动模式下平移到 B 点上方的高度，然后下降到 B 点的位置。
在 MOVJ 运动模式下下降到 B 点的位置。如图所示。

将 matlab 实验模拟中的五个点设置为演示器模式。如图所示

2. DoBot Python 程序

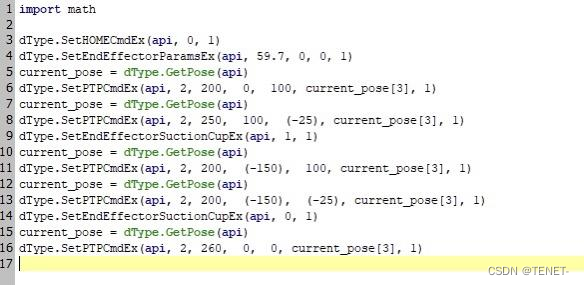
Dobot 机械臂还支持用 Python 进行二次编程，以实现各种功能。同样，利用 matlab 实验中的五个点进行轨迹规划，并在 studio 中使用 Python 编程。为了严谨起见，我添加了初始化功能。将在初始化完成后执行。代码如图（9）所示

总结

实验首先使用 D-H 方法对四自由度 Dobot 进行建模，并使用两种方法求解正运动学方程和逆运动学方程，最后使用机器人工具箱工具箱分析工作空间并仿真 Dobot 的轨迹规划，得到了 Dobot 各关节的角度、速度和加速度数据曲线。对仿真结果的分析证明了轨迹规划的合理性和可行性。
Matlab 和机器人工具箱可以对机器人进行运动学仿真，在计算机上验证机器人是否能准确地按照所需的轨迹运行。这样就可以找到运动空间，评估机械臂是否可以安全移动。