简介
ArtCoder能够从原始图像(内容)、目标图像(风格)以及想要嵌入的信息中,生成具有艺术风格的二维码。这一过程类似于通常的图像风格转换,但特别针对二维码的特点进行了优化和调整。
通过这种方法,不仅能够保持二维码的功能性和可读性,同时还能够使其具有独特的视觉效果和艺术表现力。这样的二维码不仅能够提供信息的快速识别和传递,还能够作为一种视觉元素,增强产品的吸引力和品牌的识别度。

论文地址:https://arxiv.org/abs/2011.07815
算法架构
模型
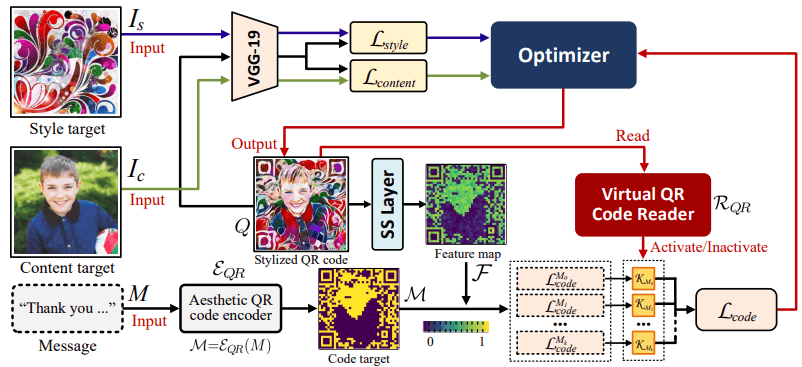
所提出的方法被建模为一个函数 P s i Psi Psi,它从风格图像 I s I_s Is、内容图像 I c I_c Ic和信息M中生成一个QR码 Q = P s i ( I s , I c , M ) Q = Psi(I_s, I_c, M) Q=Psi(Is,Ic,M)。在这个模型中,生成的QR码Q的目标函数(损失函数)Ltotal由以下方程定义,它结合了三个不同的损失函数:
L t o t a l = l a m b d a 1 L s t y l e ( I s , Q ) + l a m b d a 2 L c o m t e n t ( I c , Q ) + l a m b d a 3 L c o d e ( M , Q ) L_{t o t a l}=l a m b d a_{1}L_{s t y l e}(I_{s},Q)+l a m b d a_{2}L_{c o m t e n t}(I_{c},Q)+l a m b d a_{3}L_{c o d e}(M,Q) Ltotal=lambda1Lstyle(Is,Q)+lambda2Lcomtent(Ic,Q)+lambda3Lcode(M,Q)
这里的 l a m b d a 1 , λ 2 , λ 3 l a m b d a_{1},\lambda_{2},\lambda_{3} lambda1,λ2,λ3是权重参数,用于表示风格损失、内容损失和代码损失在总损失函数中的相对重要性。
-
风格损失Lstyle用于确保生成的QR码Q保留了风格图像Is的视觉风格。这通常通过比较风格图像和生成的QR码之间的风格特征来实现,例如使用预训练的神经网络(如VGG网络)提取特征并计算它们之间的差异。
-
内容损失Lcontent用于保证生成的QR码Q与内容图像Ic在视觉上保持一致。这通常涉及到计算两个图像之间的像素级差异,以确保内容图像的主要视觉元素被保留在最终的QR码中。
-
代码损失Lcode则专注于确保生成的QR码Q正确地编码了信息M。这通常通过验证解码后的QR码是否能够准确还原出原始信息来实现。
通过优化这个目标函数,我们可以生成既具有艺术性又能够准确传递信息的QR码。这种方法不仅提升了二维码的艺术价值,还拓宽了其在不同领域的应用潜力,如品牌营销、个人表达、艺术创作等。通过调整 l a m b d a 1 , λ 2 , λ 3 l a m b d a_{1},\lambda_{2},\lambda_{3} lambda1,λ2,λ3的值,可以根据具体需求调整风格、内容和信息的相对重要性,从而生成满足特定要求的QR码。
风格损失Lstyle和内容损失Lcontent
样式损失Lstyle和内容损失Lcontent用于确保生成的QR码保留其样式和内容。具体来说,根据现有的关于风格转换的研究(1,2),它们由以下公式定义
L s t y l e ( I s , Q ) = 1 C s H s W s ∣ ∣ G [ f s ( I s ) ] − G [ f s ( Q ) ] ∣ ∣ 2 2 {\cal L}_{s t y l e}(I_{s},Q)=\frac{1}{C_{s}H_{s}W_{s}}||G[f_{s}(I_{s})]-G[f_{s}(Q)]||_{2}^{2} Lstyle(Is,Q)=CsHsWs1∣∣G[fs(Is)]−G[fs(Q)]∣∣22
L c o n t e n t ( I c , Q ) = 1 C s H s W s ∣ ∣ f c ( I c ) ∣ − f c ( Q ) ∣ ∣ 2 2 {\cal L}_{c o n t e n t}(I_{c},Q)=\frac{1}{C_{s}H_{s}W_{s}}||f_{c}(I_{c})|-f_{c}(Q)||_{2}^{2} Lcontent(Ic,Q)=CsHsWs1∣∣fc(Ic)∣−fc(Q)∣∣22
其中G是Gram matrix, f s ( , f c ) f_s(,f_c) fs(,fc)表示从预训练的VGG-19的s(,c)层提取的特征图。
代码损失Lcode
代码损失 L c o d e L_{code} Lcode用于控制生成的QR码的内容,使用SS层(采样-模拟层),一个虚拟的QR码阅读器,模拟QR码阅读器的采样过程。
模拟层
在用于解码二维码的Goole ZXing中,二维码阅读器对每个模块的中心像素(二维码中的黑色和白色方块)进行采样和解码。
当QR码被QR码阅读器实际读取时,居住在坐标(i,j)、原点在每个模块中心的像素被采样的概率gMk(i,j)被认为遵循以下公式
g M k ( i , j ) ≡ 1 2 π σ 2 e − i 2 + j 2 2 σ 2 g_{M_{k}{(i,j)}}\equiv\,\frac{1}{2\pi\sigma^{2}}e^{-\frac{i^{2}+j^{2}}{2\sigma^{2}}} gMk(i,j)≡2πσ21e−2σ2i2+j2
采样-模拟层使用上述方程来模拟生成的QR码被真正的QR码阅读器读取时的采样过程,从而提高QR码读取过程的稳健性。
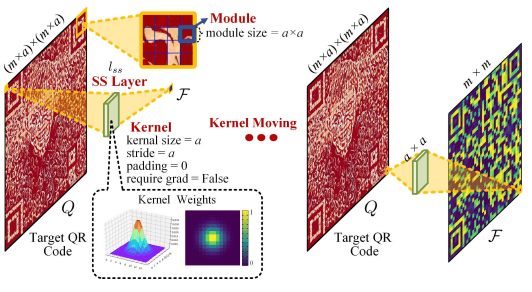
具体来说,对于QR码中的每个模块 m − d i s − m m−dis−m m−dis−m(每个模块有 a − d i s − a a−dis−a a−dis−a像素),以核大小a、跨度a和填充0进行卷积运算,并输出 m − d i s − m m−dis−m m−dis−m的特征图 F = l s S ( Q ) F=l_sS(Q) F=lsS(Q)。
基于这个特征图 F = l s S ( Q ) F=l_sS(Q) F=lsS(Q)和 g M k ( i , j ) gM_{k(i,j)} gMk(i,j),对应于模块 M k M_k Mk的位 F M k F_{Mk} FMk由以下公式给出
F M k = s u m ( i , j ) ∈ M k g M k ( i , j ) ⋅ Q M k ( i , j ) F_{M_{k}}=\,s u m_{(i,j)\in M_{k}}g_{M_{k}(i,j)}\cdot Q_{M_{k}(i,j)} FMk=sum(i,j)∈MkgMk(i,j)⋅QMk(i,j)
考虑FMk来模拟当QR码被QR码阅读器实际读取时,每个模块是否会被解码为0或1。
代码损失
代码损失 L c o d e L_{code} Lcode被计算为对应于QR码Q的每个模块 M k / i n Q M_k/inQ Mk/inQ的子码损失 L c o d e M K L_{code}^{MK} LcodeMK之和。
L c o d e = s u m M k i n Q L c o d e M k L_{c o d e}=s u m_{M_{k}i n Q}L_{c o d e}^{M_{k}} Lcode=sumMkinQLcodeMk其中 L c o d e M k L^{Mk}_{code} LcodeMk由以下公式给出。
L c o l e M k = K M k ⋅ ∣ ∣ t e x t i t M M k − F M k ∣ ∣ {\cal L}_{c o l e}^{M_{k}}=K_{M_{k}}\cdot\left|\left|t e x t i t{\cal M}_{M_{k}}-F_{M_{k}}\right|\right| LcoleMk=KMk⋅∣∣textitMMk−FMk∣∣
其中textitM是一个m×m矩阵,代表目标QR码以及每个模块是否应该为0或1。而K是由下面描述的竞争机制计算的激活图。
竞争机制
通过控制激活图K,竞争机制决定是优先考虑生成的QR码的视觉质量( L s t y l e , L c o n t e n t L_{style},L_{content} Lstyle,Lcontent),还是优先考虑QR码是否能被QR码阅读器准确读取( L c o d e L_{code} Lcode)进行优化。
这种竞争机制的管道如下图所示。

具体来说,当虚拟二维码阅读器RQR读取二维码Q时,如果模块Mk是正确的,激活图K为0,如果它是错误的,则为1。
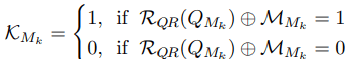
通过采用这样的竞争机制,通过优先优化错误模块的Lcode和正确模块的Lstyle,Lcontent,适当地保留了图像的质量和QR码阅读的稳健性。读取QR码时的稳健性。
虚拟QR码阅读器 R Q R R_{QR} RQR
当一个普通的二维码阅读器读取一个二维码Q时,它被转换成灰度,并根据每个模块的值进行二进制化,如下所示:
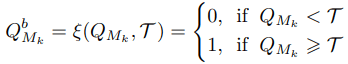
这里,T是判断一个模块是黑是白的阈值。
另一方面,当用虚拟二维码阅读器读取二维码Q时,对每个模块 M k M_k Mk进行以下二值化。

其中 T b , T w T_b,T_w Tb,Tw分别是判断模块是黑色还是白色的阈值(如果模块 M k M_k Mk是黑色的( t e x t i t M M k = 0 textitM_{Mk}=0 textitMMk=0),阈值为 T b T_b Tb,如果相反则为 T w T_w Tw)。
换句话说,根据每个模块的理想值( M M k M_{Mk} MMk)使用不同的阈值,每个模块的值比实际的二维码阅读更严格地被分辨出来。
在这种情况下,引入了一个参数 e t a = ∣ T − T b ∣ T = ∣ T w − T ∣ ( 255 − T ) e t a={\frac{\vert T-T_{b}\vert}{T}}={\frac{\vert T_{w}-T\vert}{(255-T)}} eta=T∣T−Tb∣=(255−T)∣Tw−T∣来表示QR码读取的稳健性。通过设置这个参数eta,可以在图像的质量和QR码读取的稳健性之间进行权衡。
基于上述,损失函数根据上述管道进行优化,并对生成的QR码进行迭代更新。
实验结果
实验设置
关于实验中使用的数据集,内容图像数据集包括100张512x512的图像(肖像、卡通、风景、动物、标志等),风格图像数据集包括30张代表不同风格的图像。
实验在NVIDIA Tesla V100 GPU上进行,超参数设置为 λ 1 = 1 0 1 5 , λ 2 = 1 0 7 , λ 3 = 1 0 2 0 λ_1=10_15,λ_2=10^7,λ_3=10^20 λ1=1015,λ2=107,λ3=1020,学习率为0.001,鲁棒参数 η = 0.6 η=0.6 η=0.6。
生成的QR码的质量
与现有方法的比较,首先,与现有的NST(神经风格转移)技术或二维码生成方法的比较结果如下

将Ours与其他方法相比较,生成结果的质量比现有的NST实例退化得更少,而且与现有的艺术风格的QR码生成方法相比,不会产生大量的点状噪声。
对于重量参数λ在重量参数中,改变lambda2的含量损失的结果显示如下。

从图中可以看出,通过改变权重参数,可以控制生成的图像。
二维码阅读的稳健性
在下面的实验中,我们将验证所生成的QR码的鲁棒性,以便被真正的应用所读取。
对稳健性的定性分析
在下面的图片中,显示了实际生成的QR码的一部分的放大图。

如果在对任何生成的图像进行二进制化处理后观察每个模块的中心(二进制结果中的蓝色和红色圆圈),你\会发现每个模块的黑白区域都被很好地分开,采样后的结果与理想结果相同。
因此,生成的二维码可以被普通的二维码阅读器稳健地读取。
对于表示稳健性的参数eta来说
改变稳健性参数eta的结果如下。
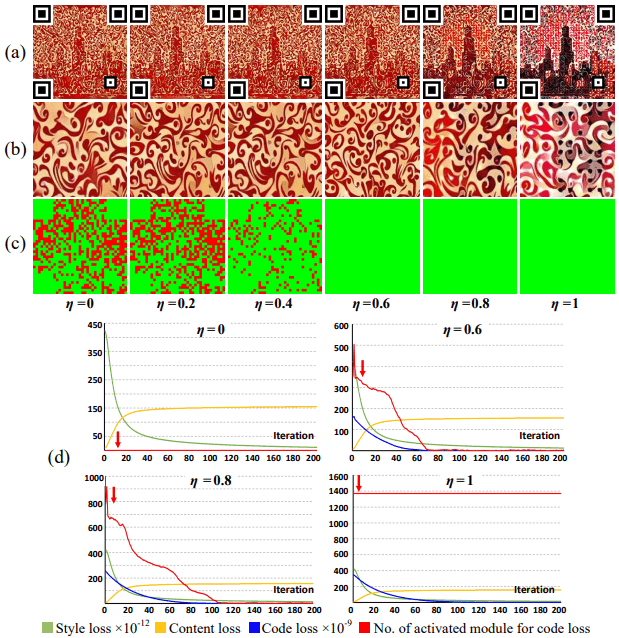
其中,(a)显示了生成的图像,(b)部分图像的放大,(c)误差模块和(d)每个损失的大小。
一般来说,增加/eta会增加编码损失,提高鲁棒性,但会降低图像质量。另一方面,较小的eta会在早期收敛为零,提高了图像质量,但降低了鲁棒性。
成功阅读的概率
生成的图像以三种尺寸(3厘米×3厘米、5厘米×5厘米和7厘米×7厘米)显示在屏幕上,扫描距离为20厘米,其结果显示如下。
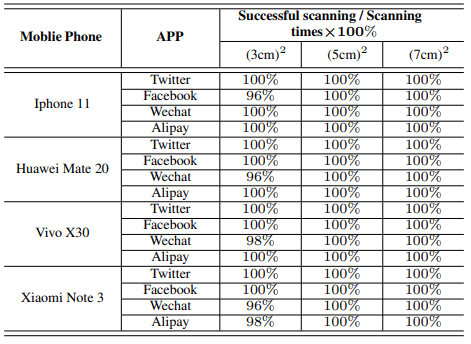
该表显示了使用每个移动设备对30个QR码进行50次扫描的平均成功次数(在3秒内成功解码被视为成功扫描)。
总的来说,它显示了至少96%的成功率,这表明所提出的方法足够强大,可以在实际应用中发挥作用。(即使在扫描失败的情况下,读取似乎也是成功的,尽管它需要3秒钟以上的时间来完成)。)
距离和角度对阅读的影响
下图显示了改变eta时的结果,并与改变距离和角度时的现有方法进行了比较。
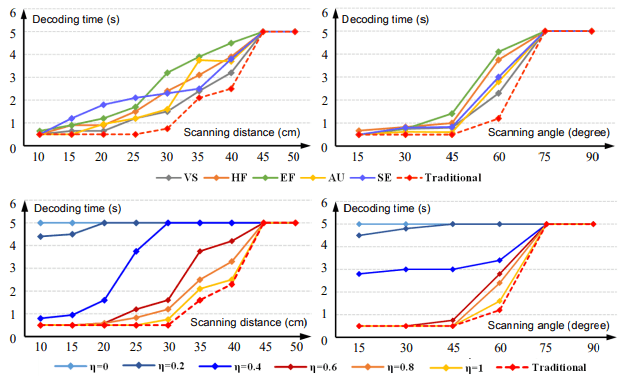
作为比较的结果,对于0.6,所提出的方法的稳健性等于或略逊于现有的方法,这意味着它的稳健性足以在实践中得到应用。
)
)
)















:APK安装包体积优化)
