技术背景
直方图是一种经常被用于统计的图形表达形式,简单来说它的功能就是用一系列的样本数据,去分析样本的分布规律。而直方图跟核密度估计(Kernel Density Estimation,KDE)方法的主要差别在于,直方图得到的是一个离散化的统计分布,而KDE方法得到的是一个连续的概率分布函数。如果将得到的分布重新用于采样,两者都可以结合蒙特卡洛方法实现这样的功能,但是KDE的优点在于它得到的结果是可微分的,那么就可以应用于有偏估计的分子动力学模拟中,如元动力学(Meta Dynamics)方法。这里主要用Python实现一个简单的KDE函数的功能,也顺带介绍一下Numpy和Matplotlib中关于直方图的使用方法。
制备样本
在使用直方图和KDE前,我们需要先制备一些样本,这里可以使用Numpy生成一些随机数,便于测试,例如均匀随机数,其概率密度为:
对应的numpy生成方法为:
data = np.random.uniform(-3, 3, (10000, ))这个分布表示在-3到3的范围内进行均匀随机采样,采10000个样本点。还可以使用高斯分布,其概率密度为:
对应的numpy生成方法为:
data = np.random.normal(0, 1, (10000, ))这个采样表示从\(\mu=0, \sigma=1\)的条件下对高斯函数进行采10000个样本点,也就是正态分布。还有一种比较常见的指数分布:
对应的numpy的采样方法为:
data = np.random.power(5, 10000)这里配置参数\(a=5\),采10000个样本点。这种采样方法,随着\(x\)的增长,概率密度会越来越大。
核密度估计函数
首先我们可以给出核密度估计函数的形式:
其中\(K(x-x_t,\sigma)\)表示一个带宽为\(\sigma\)的核函数,比如这里我们可以选用前面提到的高斯函数(或者简化为正态分布),用其他的函数作为波包也是可以的。值得注意的是,这里的带宽\(\sigma\)可以理解为波包宽度的设定。从高斯函数的表达形式也可以看出来,当\(x=\mu\)时\(f(x)\)取得最大值\(f_{max}=\frac{1}{\sqrt{2\pi}\sigma}\),\(\sigma\)的值越大,\(f_{max}\)的值就越小,那么波包的辐射范围就会越广,也就是所谓的带宽越大。
按照KDE的这种算法,假定我们用高斯函数为核函数,那么理论上应该用一个for循环来实现:
for t in range(0, M):for index in range(0, len(grids)):grids[index] += omega[t] * gaussian(x[index] - xt, sigma)但是因为在Numpy中支持了自动广播的机制,因此我们只需要一行代码就可以完成整个for循环里面的计算:
grids = gaussian(z[None] - x[:, None], sigma=sigma).sum(axis=0)完整示例
我们可以先用一个小样本示例,看一下核密度估计函数到底在做什么:
import numpy as np
import matplotlib.pyplot as pltdef gaussian(x, mu=0, sigma=1):“”“高斯波包函数“””return np.exp(-(x-mu)**2/2/sigma**2)/np.sqrt(2*np.pi)/sigmadef kde(x, grid_min, grid_max, bins, sigma):“”“带归一化的核密度估计函数”“”grid_size = (grid_max - grid_min) / binsz = grid_size*np.arange(bins) + grid_min + grid_size/2res = gaussian(z[None]-x[:, None], sigma=sigma).sum(axis=0) / x.shape[-1]res /= res.sum()*grid_sizereturn res, zplt.figure(figsize=(10, 9))
plt.title('Kernel Density Estimation')
# 正态分布采样
data = np.random.normal(0, 1, (3, ))
# Numpy生成的直方图参数
hist, bin_edges = np.histogram(data, bins=20, normed=True)
subplot1 = plt.subplot2grid((4, 3), (0, 0))
subplot1.set_title("Matplotlib Hist")
subplot1.set_ylabel("Normal Distribution")
# Matplotlib自带的直方图
subplot1.hist(data, bins=20, rwidth=0.9, color='black', density=True)
subplot2 = plt.subplot2grid((4, 3), (0, 1))
subplot2.set_title("Numpy Histogram")
subplot2.bar(bin_edges[:-1], hist, width=0.15, color='green', align='center')
subplot3 = plt.subplot2grid((4, 3), (0, 2))
subplot3.set_title("KDE Function")
# 三种不同带宽的核密度估计函数
k, z = kde(data, -3, 3, 30, 0.2)
subplot3.plot(z, k, color='orange', label=r'$\sigma$=0.2')
k, z = kde(data, -3, 3, 30, 0.6)
subplot3.plot(z, k, color='purple', label=r'$\sigma$=0.6')
k, z = kde(data, -3, 3, 30, 1.0)
subplot3.plot(z, k, color='red', label=r'$\sigma$=1.0')
subplot3.legend()
# 有偏置的正态分布
data = np.random.normal(0, 1, (3, )) + 1
hist, bin_edges = np.histogram(data, bins=20, normed=True)
subplot1 = plt.subplot2grid((4, 3), (1, 0))
subplot1.set_ylabel("Bias Normal Distribution")
subplot1.hist(data, bins=20, rwidth=0.9, color='black', density=True)
subplot2 = plt.subplot2grid((4, 3), (1, 1))
subplot2.bar(bin_edges[:-1], hist, width=0.15, color='green', align='center')
subplot3 = plt.subplot2grid((4, 3), (1, 2))
k, z = kde(data, -3, 3, 30, 0.2)
subplot3.plot(z, k, color='orange', label=r'$\sigma$=0.2')
k, z = kde(data, -3, 3, 30, 0.6)
subplot3.plot(z, k, color='purple', label=r'$\sigma$=0.6')
k, z = kde(data, -3, 3, 30, 1.0)
subplot3.plot(z, k, color='red', label=r'$\sigma$=1.0')
subplot3.legend()
# 指数分布
data = np.random.power(5, 3)*7-4
hist, bin_edges = np.histogram(data, bins=20, normed=True)
subplot1 = plt.subplot2grid((4, 3), (2, 0))
subplot1.set_ylabel("Exponential Distribution")
subplot1.hist(data, bins=20, rwidth=0.9, color='black', density=True)
subplot2 = plt.subplot2grid((4, 3), (2, 1))
subplot2.bar(bin_edges[:-1], hist, width=0.15, color='green', align='center')
subplot3 = plt.subplot2grid((4, 3), (2, 2))
k, z = kde(data, -3, 3, 30, 0.2)
subplot3.plot(z, k, color='orange', label=r'$\sigma$=0.2')
k, z = kde(data, -3, 3, 30, 0.6)
subplot3.plot(z, k, color='purple', label=r'$\sigma$=0.6')
k, z = kde(data, -3, 3, 30, 1.0)
subplot3.plot(z, k, color='red', label=r'$\sigma$=1.0')
subplot3.legend()
# 均匀分布
data = np.random.uniform(-3, 3, (3, ))
hist, bin_edges = np.histogram(data, bins=20, normed=True)
subplot1 = plt.subplot2grid((4, 3), (3, 0))
subplot1.set_ylabel("Uniform Distribution")
subplot1.hist(data, bins=20, rwidth=0.9, color='black', density=True)
subplot2 = plt.subplot2grid((4, 3), (3, 1))
subplot2.bar(bin_edges[:-1], hist, width=0.15, color='green', align='center')
subplot3 = plt.subplot2grid((4, 3), (3, 2))
k, z = kde(data, -3, 3, 30, 0.2)
subplot3.plot(z, k, color='orange', label=r'$\sigma$=0.2')
k, z = kde(data, -3, 3, 30, 0.6)
subplot3.plot(z, k, color='purple', label=r'$\sigma$=0.6')
k, z = kde(data, -3, 3, 30, 1.0)
subplot3.plot(z, k, color='red', label=r'$\sigma$=1.0')
subplot3.legend()
# 画图
plt.show()得到的结果如下图所示:

在这个结果中我们看到,因为采样比较稀疏,直方图只会显示被采到的那个格点,而核密度估计函数则是以波包的形式,将采样概率密度辐射到整个的采样空间上,这就实现了一个连续化。如果把采样密度调大一点,比如我们调整为采样10000次,那么得到的结果是这样的:
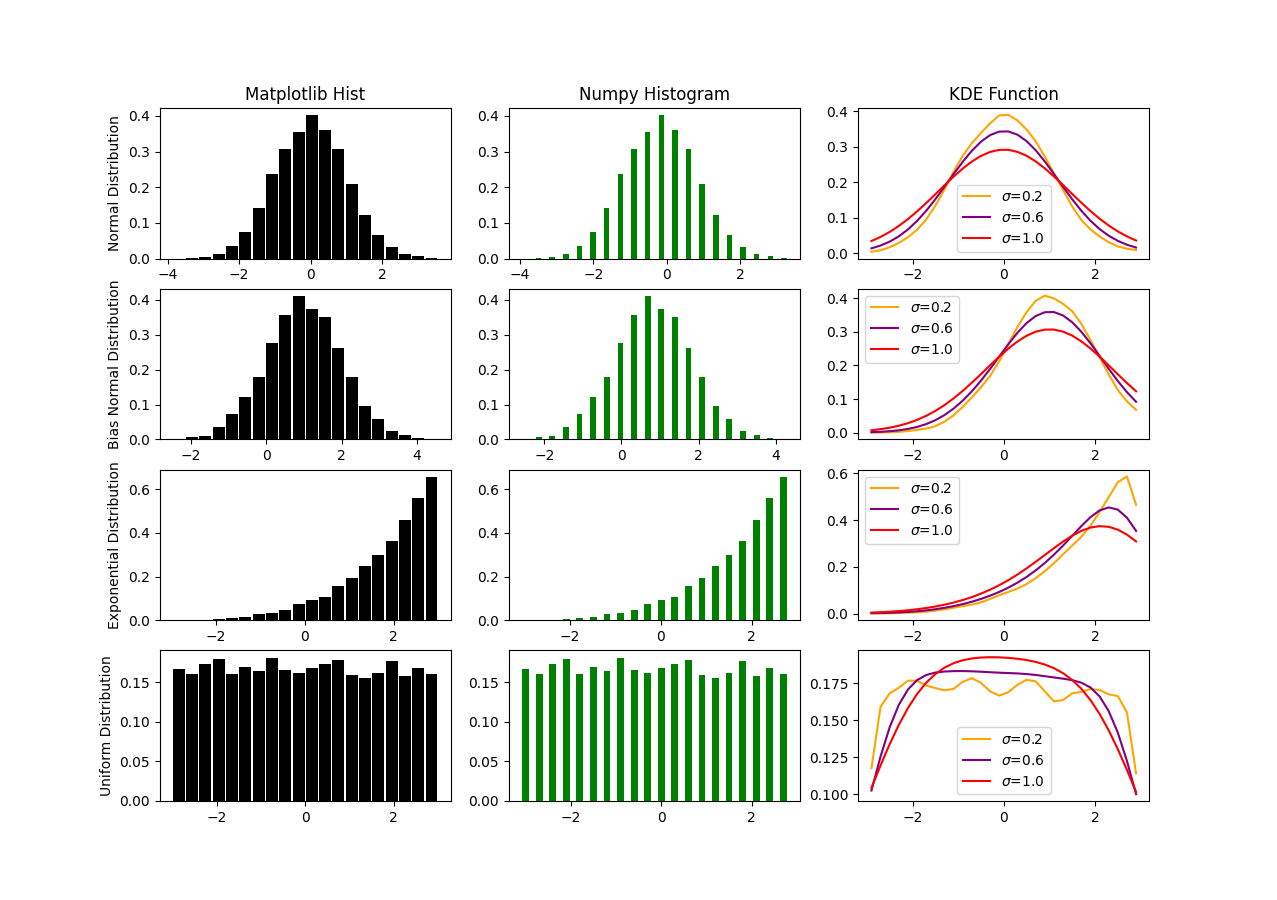
这也表明,只有足够多的样本数量,才能够相对准确的复原出采样的分布函数,而且这跟边界条件的连续性有比较大的关系。
总结概要
核密度估计(KDE)方法,相当于用多个波包的组合形式来近似一个真实的概率密度,以获得一个连续可微分的概率密度函数。本文通过一些简单的概率分布的示例,演示了一下KDE的使用方法。其实KDE的思想在很多领域都会以不同的形式出现,是一个比较基础的概率分布近似手段。
版权声明
本文首发链接为:https://www.cnblogs.com/dechinphy/p/kde.html
作者ID:DechinPhy
更多原著文章:https://www.cnblogs.com/dechinphy/
请博主喝咖啡:https://www.cnblogs.com/dechinphy/gallery/image/379634.html




![[Linux][进程间通信][一][匿名管道][命名管道]详细解读](http://pic.xiahunao.cn/[Linux][进程间通信][一][匿名管道][命名管道]详细解读)


)











