题目
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
- 输入:n = 4
- 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
- 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
- 输入:n = 1
- 输出:[["Q"]]
思路
都知道n皇后问题是回溯算法解决的经典问题,但是用回溯解决多了组合、切割、子集、排列问题之后,遇到这种二维矩阵还会有点不知所措。
首先来看一下皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。下面我用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:
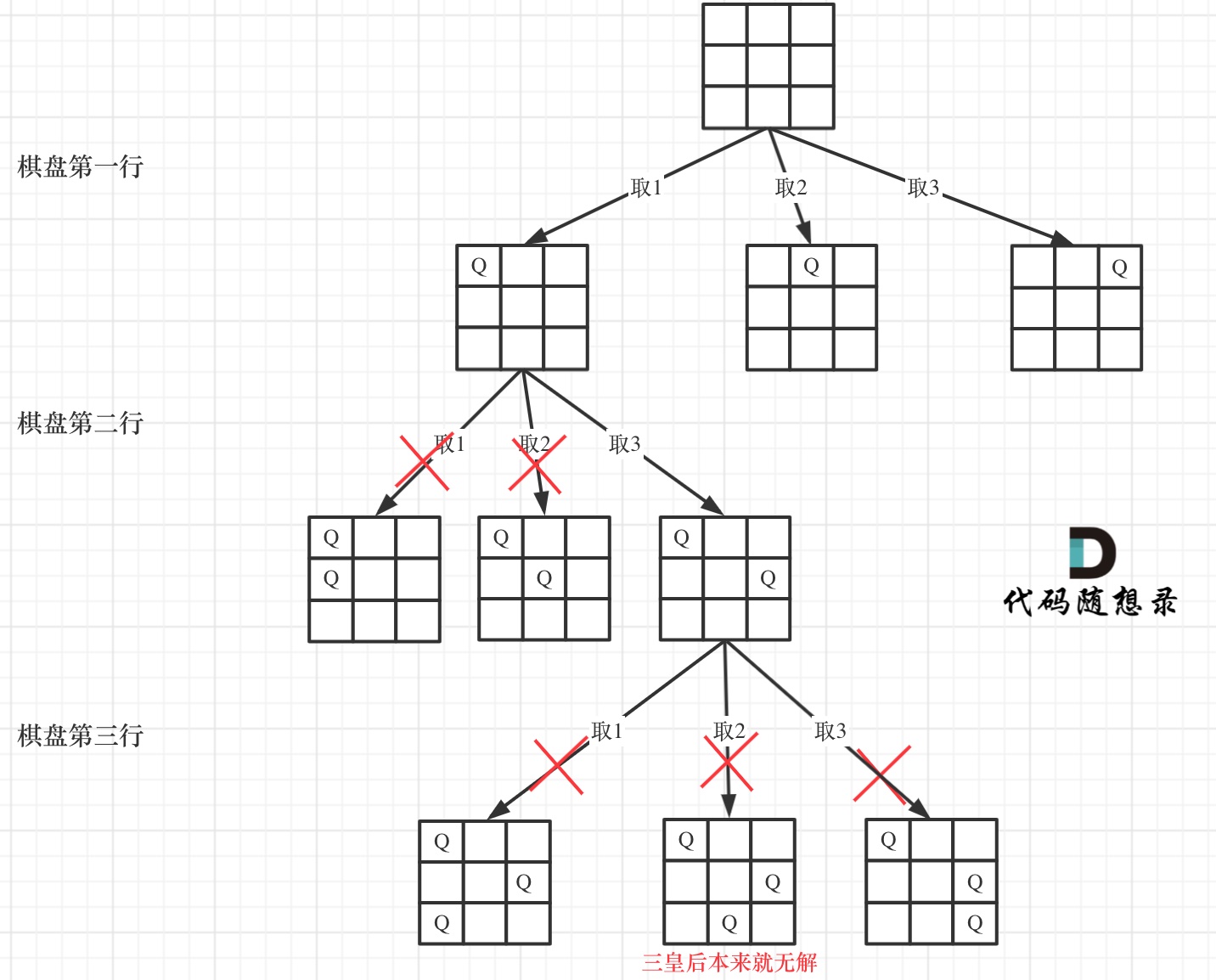
从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。那么我们用皇后们的约束条件,来回溯搜索这棵树,只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了。
回溯三部曲
1、递归函数参数
我依然是定义全局变量二维数组result来记录最终结果。
参数n是棋盘的大小,然后用row来记录当前遍历到棋盘的第几层了。
代码如下:
vector<vector<string>> result;
void backtracking(int n, int row, vector<string>& chessboard) {
2、递归终止条件
在如下树形结构中:
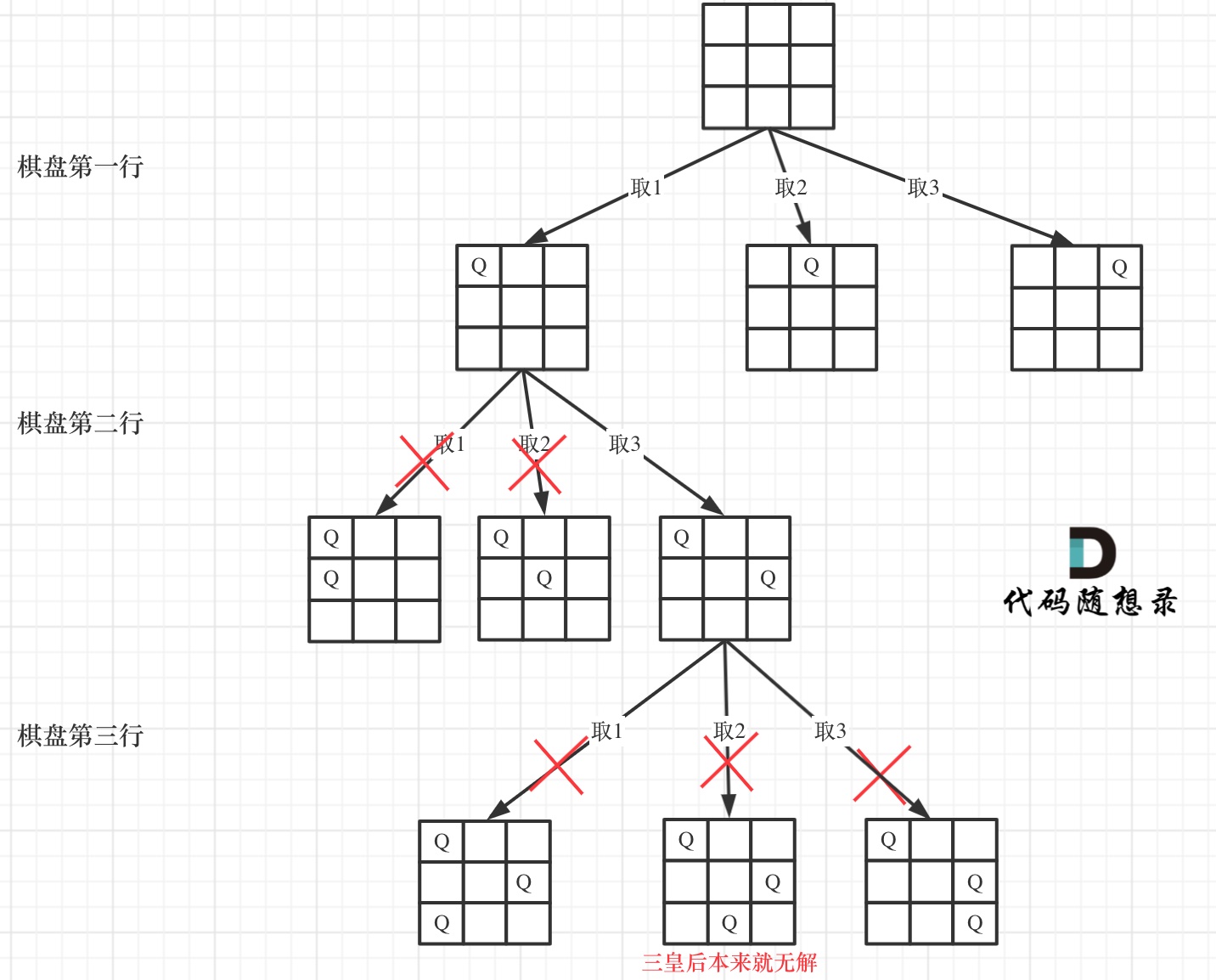
可以看出,当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了。
代码如下:
if (row == n) {result.push_back(chessboard);return;
}
3、单层搜索的逻辑
递归深度就是row控制棋盘的行,每一层里for循环的col控制棋盘的列,一行一列,确定了放置皇后的位置。每次都是要从新的一行的起始位置开始搜,所以都是从0开始。
for (int col = 0; col < n; col++) {if (isValid(row, col, chessboard, n)) { // 验证合法就可以放chessboard[row][col] = 'Q'; // 放置皇后backtracking(n, row + 1, chessboard);chessboard[row][col] = '.'; // 回溯,撤销皇后}
}
验证棋盘是否合法
按照如下标准去重:
- 不能同行
- 不能同列
- 不能同斜线 (45度和135度角)
代码如下:
bool isValid(int row, int col, vector<string>& chessboard, int n) {// 检查列for (int i = 0; i < row; i++) { // 这是一个剪枝if (chessboard[i][col] == 'Q') {return false;}}// 检查 45度角是否有皇后for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {if (chessboard[i][j] == 'Q') {return false;}}// 检查 135度角是否有皇后for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {if (chessboard[i][j] == 'Q') {return false;}}return true;
}
在这份代码中,细心的同学可以发现为什么没有在同行进行检查呢?因为在单层搜索的过程中,每一层递归,只会选for循环(也就是同一行)里的一个元素,所以不用去重了。
那么按照这个模板不难写出如下C++代码:
class Solution {
private:
vector<vector<string>> result;
// n 为输入的棋盘大小
// row 是当前递归到棋盘的第几行了
void backtracking(int n, int row, vector<string>& chessboard) {if (row == n) {result.push_back(chessboard);return;}for (int col = 0; col < n; col++) {if (isValid(row, col, chessboard, n)) { // 验证合法就可以放chessboard[row][col] = 'Q'; // 放置皇后backtracking(n, row + 1, chessboard);chessboard[row][col] = '.'; // 回溯,撤销皇后}}
}
bool isValid(int row, int col, vector<string>& chessboard, int n) {// 检查列for (int i = 0; i < row; i++) { // 这是一个剪枝if (chessboard[i][col] == 'Q') {return false;}}// 检查 45度角是否有皇后for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {if (chessboard[i][j] == 'Q') {return false;}}// 检查 135度角是否有皇后for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {if (chessboard[i][j] == 'Q') {return false;}}return true;
}
public:vector<vector<string>> solveNQueens(int n) {result.clear();std::vector<std::string> chessboard(n, std::string(n, '.'));backtracking(n, 0, chessboard);return result;}
};
- 时间复杂度: O(n!)
- 空间复杂度: O(n)
下面给出笔者自己的c++代码与大家分享,思路大体和上面的差不多,但是也不尽相同,其中我用一个q_count代表当前已经放置的皇后数目,同时也代表了当前回溯树的深度,另外最主要的差别就是我用一个pos数组代表了棋盘每一行上皇后所在位置,最后输出结果时就需要用gouzao函数将这些位置信息转换成vector<string>虽然多了一个步骤,但是这对于判断当前位置放置皇后是否合法会有很大程度上的精简,代码如下:
class Solution {
public:vector<vector<string>> result;vector<string> path;int q_count=0;int pos[10] = {-1};bool is_ok(int x,int y){for (int i = 0 ; i < x ; i++){if(y == pos[i] || abs(x-i) == abs(y - pos[i]))return false;}return true;}void gouzao(int n){path.clear();string tmp;for(int i = 0 ; i< n ; i++){for(int j = 0 ; j < n ; j++){if(j == pos[i]) tmp+='Q';else tmp+='.';}if(!tmp.empty()) path.push_back(tmp);tmp.clear();}result.push_back(path);}void backtracing(int n){if(q_count == n){gouzao(n); return;}for(int i = 0 ; i < n ; i++){if(!is_ok(q_count,i)) continue;pos[q_count++] = i;backtracing(n);q_count--;pos[q_count] = -1;}}vector<vector<string>> solveNQueens(int n) {backtracing(n);return result;}
};可以看到我这里判断合法的语句只有一句if(y == pos[i] || abs(x-i) == abs(y - pos[i])),其中x和y代表当前位置的坐标,pos数组代表每一行中皇后的位置索引,具体判断方法就是遍历之前已经放置过的每一行,如果遇到y == pos[i],既在第i行的y列已经有皇后了,那么不合法,或者abs(x-i) == abs(y - pos[i]),既当前位置的斜向也已经有皇后则也不合法,后一个条件需要大家理解一下,两个坐标在同一个斜线代表两坐标连线与水平的夹角为45度,通过斜率公式便可以写出上面的条件,不理解的可以在纸上画一画加深理解。



 函数)




cyberrealisticXL_v11VAE.safetensors)



)
)






