面试经典150题——从前序与中序遍历序列构造二叉树

aerial photo of mountain range

1. 题目描述

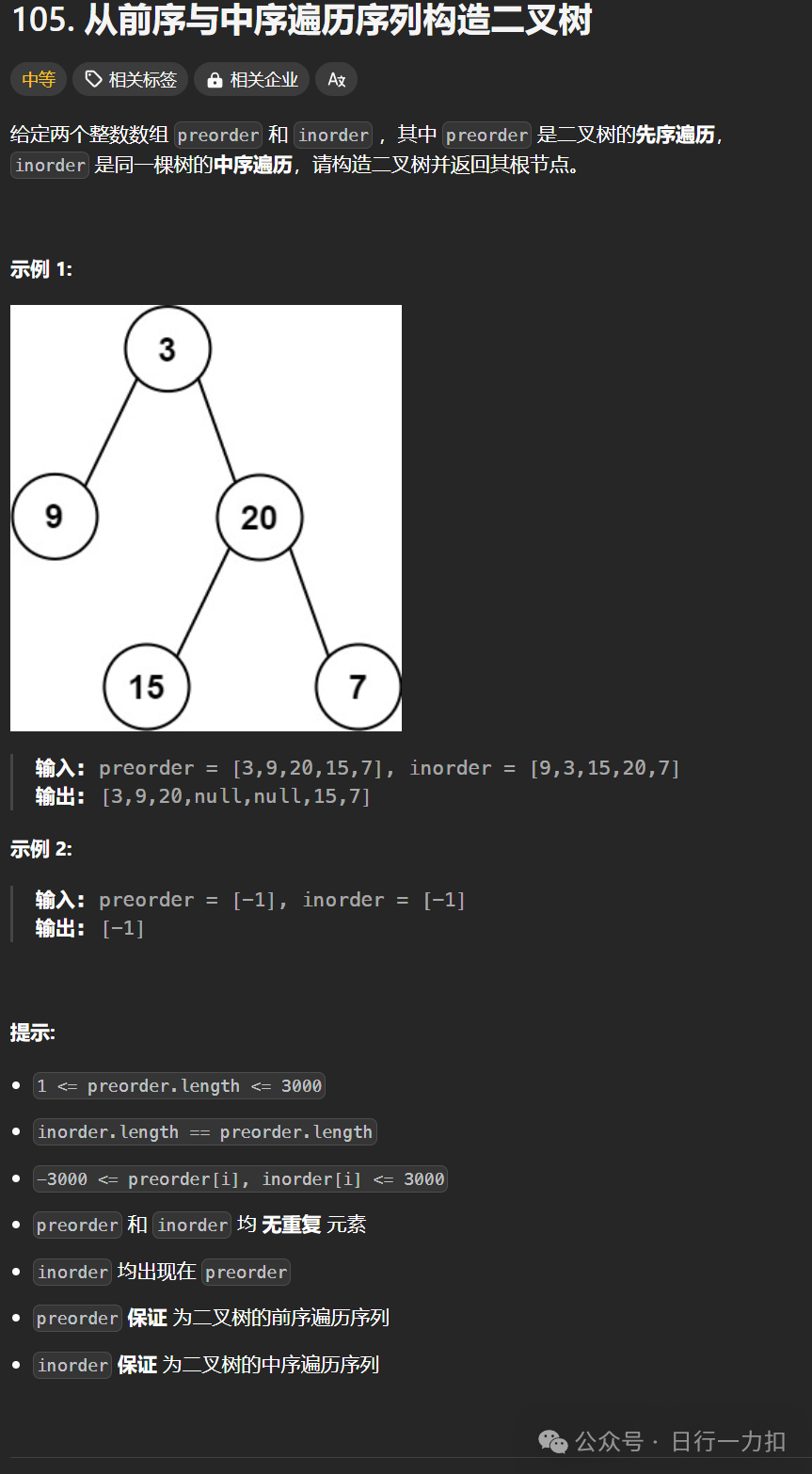
2. 题目分析与解析

二叉树的前序、中序和后序遍历

二叉树的前序、中序和后序遍历是树的三种基本遍历方式，它们是通过不同的顺序来访问树中的节点的。

前序遍历（Pre-order traversal）：

访问根节点

前序遍历左子树

前序遍历右子树

中序遍历（In-order traversal）：

中序遍历左子树

访问根节点

中序遍历右子树

后序遍历（Post-order traversal）：

后序遍历左子树

后序遍历右子树

访问根节点

每种遍历方式都有其特定的应用场景，以及在不同问题中的实用性。

前序遍历常用于复制二叉树、计算表达式树的值等。

中序遍历常用于搜索树（如二叉搜索树）中，可以按照从小到大的顺序访问所有节点。

后序遍历通常用于释放二叉树的内存空间。

根据题目要求，我们可以从以下几个方面着手：

理解二叉树的性质：

通过这些性质，根节点在前序遍历中是容易找到的，而中序遍历中根节点的位置可以用来划分左子树和右子树。
- 前序遍历（Preorder Traversal）的特点是根节点首先出现，接着是左子树的所有节点，最后是右子树的所有节点。
- 中序遍历（Inorder Traversal）的特点是先遍历左子树，然后是根节点，最后是右子树。
使用哈希映射优化搜索：
- 而在中序遍历中频繁查找节点位置是一个时间复杂度较高的操作（O(n)），为了提升效率，可以使用哈希映射（HashMap）存储每个值与其在中序遍历中的索引。这样，节点位置的查找时间复杂度可以降低到O(1)。
- 因为题目中提到了：
递归构建二叉树：

为什么使用递归求解？因为构建一棵二叉树无非就是三个步骤：创建根节点，构建左子树，构建右子树。因此这个问题就可以按照如下求解：

但是注意递归求解肯定有返回条件，这个返回条件就是左边界大于右边界，也就是子树节点个数小于等于0的时候代表没有左子树了，返回null。所以有如下：
- 递归基：如果前序遍历的子区间为空（即左边界大于右边界），这意味着没有子树可以构建，返回null。
- 创建根节点：前序遍历的第一个节点总是根节点，使用这个性质创建当前的根节点。
- 计算左子树的大小：根据根节点在中序遍历中的位置和左边界的差值，可以确定左子树的节点数目。
- 递归构建左子树：在前序遍历中，紧接根节点之后的一段连续序列对应于左子树的前序遍历，而在中序遍历中，根节点位置之前的一段序列对应于左子树的中序遍历。利用这两个序列，递归构建左子树。
- 递归构建右子树：类似地，根据前序和中序遍历中左子树节点数的信息，可以确定右子树的前序和中序遍历序列，进而递归构建右子树。
1. 构建根节点
2. 找到左子树的部分构建左子树
3. 找到右子树的部分构建右子树
4. 返回根节点

3. 代码实现

4. 相关复杂度分析

时间复杂度

哈希映射构建：
- 遍历中序数组以构建哈希映射，时间复杂度为 (O(n))，其中 (n) 是树中节点的数量。
递归构建二叉树：
- 每次递归调用处理一个节点（根节点），因此每个节点会被访问一次。
- 虽然递归多次，但每个节点仅在其对应的递归层次中处理一次，因此总的时间复杂度为 (O(n))。

总的时间复杂度：由于哈希映射的构建和递归构建树各占 (O(n))，总时间复杂度是 (O(n))。

空间复杂度

哈希映射：
- 哈希映射存储所有节点及其在中序遍历中的索引，占用 (O(n)) 的空间。
递归调用栈：
- 最坏情况下，二叉树是高度不平衡的，例如全部倾斜成一条直线，这时递归的深度为 (n)，因此调用栈的最大深度也为 (O(n))。
- 如果树是平衡的，递归的深度大约是 (log n)。
递归中的临时变量：
- 在每次递归调用中，使用了一些额外的空间来存储诸如 preorder_left, preorder_right, inorder_left, inorder_right, inorder_root_index 和 left_tree_size 等变量，但这些都是常数空间，因此不影响总体空间复杂度。