T04BF
👋专栏: 算法|JAVA|MySQL|C语言
🫵 小比特 大梦想

此篇文章与大家分享分治递归、搜索与回溯算法中关于二叉树的深搜的专题
如果有不足的或者错误的请您指出!

1.计算布尔值的二叉树

题目:计算布尔值的二叉树

1.1解析

这道题实际上就是二叉树深度优先遍历的体现,我们想知道根节点的布尔值,就需要由根节点的left 和 right 和 根节点的值有关
那么我们就需要先求出root.left 和 root.right 的布尔值,这就是深度优先遍历
而其中我们可以很容易发现一个"子问题",就是求出root.left 和 root.right 的布尔值,那么就可以通过递归来做
那么递归的出口是什么?? 就是找到叶子结点

1.2题解

    public boolean evaluateTree(TreeNode root) {if(root.val == 0) {return false;}if(root.val == 1) {return true;}boolean left = evaluateTree(root.left);boolean right = evaluateTree(root.right);return (root.val == 2) ? (left || right) : (left && right);}

2.求根节点到叶子节点数字之和

题目:求根节点到叶子节点的数字之和

2.1解析

实际上也是深度优遍历的体现,我们要知道根节点要叶子节点的数字之和,就要用求出根节点的 left到叶子节点的数字之和 加上 根节点的 right到叶子节点的数字之和.同样可以用递归来做
其中有一个细节就是,我们此时不是简单的求出各个节点的数字之和,是拼接起来的
我们可以将上层节点的节点值 通过传参的方式来实现拼接
如下图所示

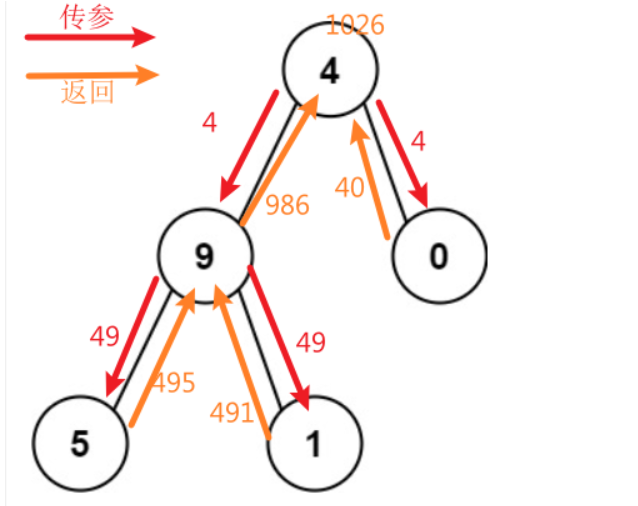
2.2题解

    private int sum(TreeNode root,int n) {int preNum = n * 10 + root.val;if(root.left == null && root.right == null) {return preNum;}int ret = 0;if(root.left != null) {ret += sum(root.left,preNum);}if(root.right != null) {ret += sum(root.right,preNum);}return ret;}public int sumNumbers(TreeNode root) {if(root == null) {return 0;}return sum(root,0);}

3.二叉树剪枝

题目:二叉树剪枝

3.1解析

我们可以采⽤后序遍历的⽅式来解决这个问题。在后序遍历中，我们先处理左子树,然后处理
右子树，最后再处理当前节点。
在处理当前节点时，我们可以判断其是否为叶⼦节点且其值是否为 0,如果为o就直接删除
就可以使用递归来做,递归的出口就是遇到叶子结点

3.2题解

    public TreeNode pruneTree(TreeNode root) {if(root == null) {return null;}root.left = pruneTree(root.left);root.right = pruneTree(root.right);if(root.left == null && root.right == null && root.val == 0) {return null;}return root;}

4.验证二叉搜索树

验证二叉搜索树

4.1解析

二叉搜索树有一个特征,就是这棵数的中序遍历结果,是一个升序的序列
那么我们就可以以中序遍历的方式来遍历这棵二叉树
一个直观的方法就是创建一个空间来存放中序遍历的结果,但是空间复杂度较高
我们实际上可以在方法外面定义一个变量preNum,将每次遍历的节点的值与preNum做比较,如果是 > preNum,那么就将preNum改为这个节点的值,如果是小于,说明不是升序,那么就要返回false
还有一个提升效率的细节问题就是

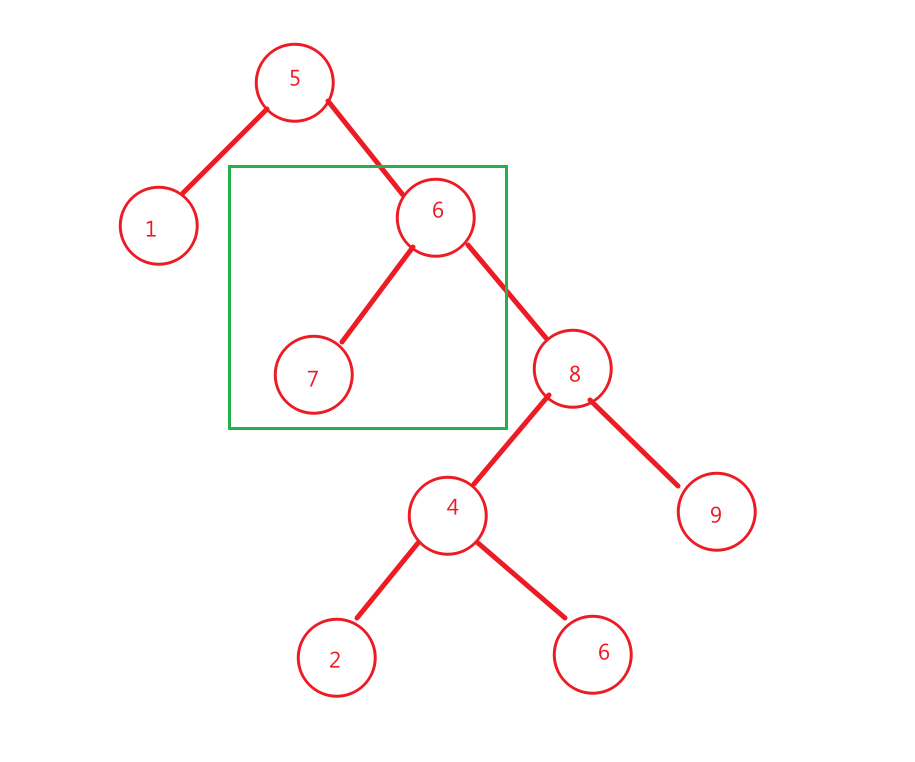
如果出现如图所示的情况,由于我们是中序遍历,遍历到绿色这一部分到时候,就发现不是一棵二叉树搜索树了,但是按照我们上面的逻辑,是需要将右边整个子树都遍历完才能返回结果
但是这样的操作是没必要的,因此我们如果在某次判断完左枝如果已经返回false,那么右枝就没必要判断了,直接返回false即可
这就是"剪枝"操作

4.2题解

    private long preNum = Long.MIN_VALUE;public boolean isValidBST(TreeNode root) {if(root == null) {return true;}boolean left = isValidBST(root.left);if(!left) {return false;//剪枝}if(preNum < root.val) {preNum = root.val;}else{return false;}boolean right = isValidBST(root.right);return left && right;}

5.二叉搜索树中第K小的元素

题目:二叉搜索树中第K小的元素

5.1解析

按照上一题提到,二叉搜索树的中序遍历结果是升序序列
那么要寻找第k小的元素,我们只需要对二叉搜索树进行中序遍历,遍历到第k个节点的时候,就是第k小的元素
我们可以在方法外定义一个变量count = k,每遍历一个节点,count–,直到k = 0,此时这个值就是我们想要的值
同样,当count = 0的时候,此时说明第k小的元素已经找到的,就不需要再遍历了,因此我们可以将这个条件加在每一次递归的前面,即"剪枝"

5.2题解

    private int count = 0;private int ret = 0;public int kthSmallest(TreeNode root, int k) {count = k;dfs(root);return ret;}private void dfs(TreeNode root) {if(root == null || count == 0) {return;}dfs(root.left);count--;if(count == 0) {ret = root.val;return;}dfs(root.right);}

6.二叉树的所有路径

题目:二叉树的所有路径

6.1解析

从根节点开始找二叉树的路径,本质上就是前序遍历的过程
但是我们此时不仅仅是简单的进行前序遍历,我们还要将当前已经遍历到的路径作为参数传递
当递归到叶子结点的时候,将当前的路径加入到返回列队中即可

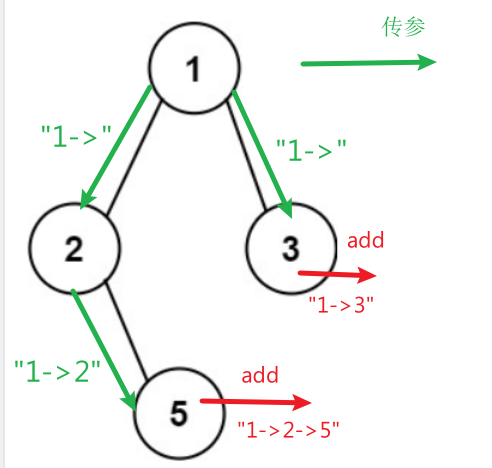
6.2题解

    List<String> ret;public List<String> binaryTreePaths(TreeNode root){ret = new ArrayList<>();dfs(root, new StringBuffer());return ret;}void dfs(TreeNode root, StringBuffer _path){StringBuffer path = new StringBuffer(_path);path.append(Integer.toString(root.val));if(root.left == null && root.right == null){ret.add(path.toString());return;}path.append("->");if(root.left != null) dfs(root.left, path);if(root.right != null) dfs(root.right, path);}

T04BF
🫵 小比特 大梦想