928. 尽量减少恶意软件的传播 II

方法1：dfs

只遍历非感染节点

从未感染的节点出发，遇到非感染节点就继续dfs，dfs过程中统计节点的个数。遇到感染节点，就更新状态。

class Solution {boolean[] vis, isInitial;int size, nodeState;public void dfs(int x, int[][] graph) {vis[x] = true;size++;for (int y = 0; y < graph[x].length; ++y) {if (vis[y]) continue;if (graph[x][y] == 0) {continue;}if (isInitial[y]) {// y是感染节点if (nodeState == -1) {nodeState = y;} else if (nodeState >= 0 && nodeState != y) {//nodeState != y: 避免在一次dfs中多次搜索到(因为可能存在多条到y的路径)，见解释1nodeState = -2;} continue;}dfs(y, graph);}}public int minMalwareSpread(int[][] graph, int[] initial) {int n = graph.length;vis = new boolean[n];isInitial = new boolean[n];Arrays.sort(initial);for (int i : initial) {isInitial[i] = true;}int[] cnt = new int[n]; // cnt[i]: cnt[i]个节点只被i这个感染节点感染，i只能是感染节点int ans = n;int maxSize = 0;for (int i = 0; i < n; ++i) {if (vis[i] || isInitial[i]) continue;size = 0;nodeState = -1; // -1:初始状态，>=x:仅找到了一个感染节点，-2:找到了多个感染节点dfs(i, graph);if (nodeState >= 0) {if (size > 0) {cnt[nodeState] += size; // 注意是累加，可能存在多个节点遍历到nodeState，而cnt[nodeState]是总的感染个数if (cnt[nodeState] > maxSize) {maxSize = cnt[nodeState];ans = nodeState;} else if (cnt[nodeState] == maxSize && nodeState < ans) {ans = nodeState;}}}}return ans == n ? initial[0] : ans;}
}

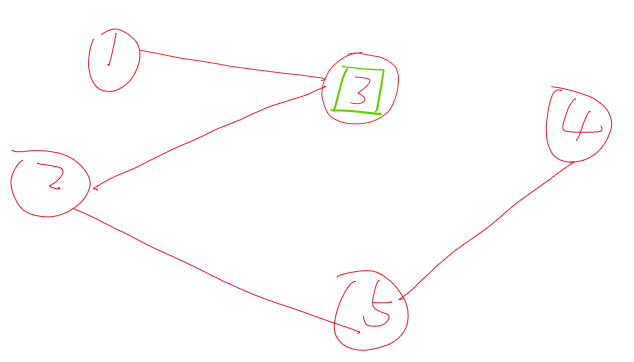
解释1：如下图，3是感染节点，到达3有两条路径，一条是经过1这个节点，另一条是经过2这个节点。如果不加nodeState != y这个判断，在第一次遍历到3这个节点时，nodeState = 3，等到第二次遍历到3这个节点时，nodeState=-2，这是不对的，因为这个同一个感染节点

方法2：并查集

构建不包含非感染节点的连通集，统计该连通集连接的感染节点个数，若为1，假设这个感染节点是i，相当于把1这个感染节点去掉后，可以避免整个连通集感染。也就是1这个感染节点可以感染的节点数。
我们计算每一个感染节点可以感染的节点数(与感染节点相连的所有连通集的节点个数累加)，取感染节点最多，且索引最小对应的感染节点

class Solution {int[] size; // 记录集合的个数boolean[] isInitial;int find(int x, int[] p) {if (x != p[x]) {p[x] = find(p[x], p);}return p[x];}public int minMalwareSpread(int[][] graph, int[] initial) {int n = graph.length;size = new int[n];Arrays.fill(size, 1);Arrays.sort(initial);isInitial = new boolean[n];int[] p = new int[n];for (int i = 0; i < n; ++i) p[i] = i;for (int i : initial) {isInitial[i] = true;}for (int i = 0; i < n; ++i) {if (isInitial[i]) continue;for (int j = i + 1; j < n; ++j) {if (isInitial[j] || graph[i][j] == 0) continue;int iFather = find(i, p);int jFather = find(j, p);if (iFather != jFather) {size[iFather] += size[jFather];p[jFather] = iFather;}}}Set<Integer>[] set = new HashSet[n]; // s[i]统计所有与i(i是感染节点)相连的连通分量的代表节点// Arrays.fill(set, new HashSet<>()); 这条语句执行后，set中所有的元素都是同一个对象(被坑惨了~~)for (int i = 0; i < n; ++i) {set[i] = new HashSet<>();}int[] cnt = new int[n]; // cnt[i]: i这个代表节点表示的连通分量连接cnt[i]个(初始)感染节点for (int i : initial) {for (int j = 0; j < graph[i].length; ++j) {if (graph[i][j] == 0 || isInitial[j]) continue; //j为非感染节点int jFather = find(j, p);set[i].add(jFather);}for (int root : set[i]) {cnt[root]++;}}   int ans = n;int maxSize = 0;for (int i : initial) {int count = 0; // 计算与i相连的所有连通图的总元素个数for (int root : set[i]) {if (cnt[root] == 1) { // 如果连通分量连接这多个感染节点，那么移除一个无法避免感染count += size[root];}}if (count > maxSize) {maxSize = count;ans = i;} else if (count == maxSize && i < ans) {ans = i;}}return ans == n ? initial[0] : ans;}
}

GCD and LCM

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>using namespace std;
typedef long long ll;ll gcd(ll a, ll b) {while (b != 0) {ll t = a % b;a = b;b = t;}return a;
}int main() {ll a, b;while (scanf("%lld%lld", &a, &b) == 2) {if (a < b) {swap(a, b);}ll g = gcd(a, b);ll l = (ll)a / g * b;printf("%lld %lld\n", g, l);}return 0;
}

Missing Bigram

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;string s;
int n;
int main() {int t;scanf("%d", &t);while (t--) {scanf("%d", &n);cin >> s;string res = s;string pre = s;for (int i = 0; i < n - 3; ++i) {string cur;cin >> cur;if (pre[1] == cur[0]) {res += cur[1];}else {res += cur;}pre = cur;}while (res.size() < n) res += "a";cout << res << endl;}return 0;
}