目录
前言:
目标
1 什么叫 假设检验
1.1 假设检验的定义
1.1.1 来自百度百科
1.1.2 维基百科
1.2 假设检验的最底层逻辑:是反证法思想
1.3 假设检验的底层构造:小概率反证法思想
2 什么叫反证法
2.1 反证法的概念
2.1.1 来自百度百科
2.2.2 维基百科
2.2 别名
2.3 相近概念
2.4 为什么要用反证法
2.5 反证法的内核
2.5.1 国内的一个文章
2.5.2 维基百科的反证法逻辑内核
1.7 用反证法的内核 梳理一遍假设检验的逻辑
3 原假设和备择假设
3.1 原假设和备择假设
3.2 什么叫 有统计学意义? (一般= p概率很小= 拒绝原假设h0)
3.3 有统计学意义和实际有意义不是一回事
4 两类错误
4.1 什么叫2类错误
4.2 这两类错误的计算公式
4.2.1 计算公式
4.2.2 下面这个医学图来源
4.2.3 和机器学习理的准确率,召唤率虽然很像,但是不是一回事。
4.2.4 第1类错误和第2类错误谁更重要?
4.2.5 两类错误不能同时消除
5 如何设计H0的一些例子和思考
5.1 对H0原假设的理解
5.2 具体的例子
6 双侧检验
7 左侧检验和右侧检验
7.1 右侧检验
7.2 左侧检验(下限检验)
8 拒绝域
8.1 双边拒绝域
8.2 右边拒绝域
8.3 左边拒绝域
前言:
之前想直接跳过这些基础知识,直接学习F检验,Z检验,T检验之类的,但是过程中发现自己很多内容,理解的很偏颇,这些基础知识很重要。现在回头来补习。
目标
- 关于假设检验的各种基础知识
- 理解假设检验的反证法
- H0是怎么设计的
- 什么时候用单侧检验或双侧检验
1 什么叫 假设检验
1.1 假设检验的定义
1.1.1 来自百度百科
- 假设检验,也称为统计假设检验,是一种统计推断方法,其目的是根据样本数据对总体做出推断。
- 假设检验的基本思想是先对总体的某个特征(如总体参数)提出一个假设,然后利用样本数据来检验这个假设是否合理。
- 如果样本数据表明假设不合理,则可以拒绝这个假设;如果样本数据表明假设合理,则可以接受这个假设。
- 这个过程基于“小概率事件”原理,认为如果一个事件发生的概率很小,那么这个事件在一次试验中几乎不可能发生。
- 因此,如果样本数据表明假设不成立,则这个假设可以被认为是“小概率事件”,不应该被接受。相反,如果样本数据表明假设成立,则这个假设可以被认为是一个“大概率事件”,应该被接受。
- 假设检验的步骤通常分为以下三个阶段:
- 提出假设。这包括一个原假设(通常用H0表示)和一个备择假设(通常用H1表示)。原假设通常是我们要检验的假设,而备择假设则是如果原假设不成立时所接受的假设。
- 计算统计量。根据样本数据计算一个统计量,这个统计量可以用来衡量样本数据与假设之间的差异。常用的统计量包括t统计量、z统计量和卡方统计量等。
- 判断假设是否合理。根据统计量的值和对应的p值来判断假设是否合理。如果p值小于预先设定的显著性水平(如0.05),则可以拒绝假设;否则,可以接受假设。
1.1.2 维基百科
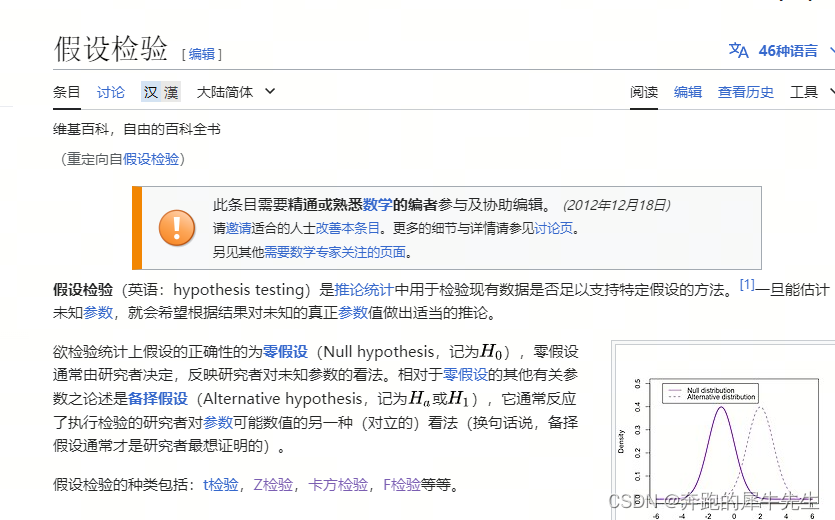
1.2 假设检验的最底层逻辑:是反证法思想
换句话说,备择假设通常才是研究者最想证明的。因此才使用反证法
假设检验也就是反证法思想,想证明这个H1对,那么只要证明H0错误就可以了。
一般统计学默认潜规则就是: 验证者都是想(预期)证明H1是对的,通过反证法故意希望去证明H0是错的,当然结果不一定能达到预期。
- 如果确实证明H0大概率(如1-α=95%)是对的,就接受H0,承认自己最初构想H1是错的
- 如果确实证明H0只有小概率如 1%是对的,那么就拒绝H0,证明了自己最初构想H1是对的。
1.3 假设检验的底层构造:小概率反证法思想
假设检验----底层思想是反证法思想,而且是小概率反证法思想
小概率思想是指小概率事件(P<0.01或P<0.05或0.1)在一次试验中基本上不会发生。
- 在原假设的前提下,如果在一次观察中小概率事件发生了,则认为假设不成立,
- 反之,如果小概率事件没有发生,则没有理由否定原假设。
2 什么叫反证法
2.1 反证法的概念
2.1.1 来自百度百科
- 反证法,亦称“逆证”,是间接论证的方法之一,是通过断定与论题相矛盾的判断(即反论题)的虚假来确立论题的真实性的论证方法。
- 反证法的论证过程如下:首先提出论题:然后设定反论题,并依据推理规则进行推演,证明反论题的虚假;最后根据排中律,既然反论题为假,原论题便是真的。
- 在进行反证中,只有与论题相矛盾的判断才能作为反论题,论题的反对判断是不能作为反论题的,因为具有反对关系的两个判断可以同时为假。
- 反证法中的重要环节是确定反论题的虚假,常常要使用归谬法。
- 反证法是一种有效的解释方法,特别是在进行正面的直接论证或反驳比较困难时,用反证法会收到更好的效果。
2.2.2 维基百科
https://zh.wikipedia.org/wiki/%E5%8F%8D%E8%AD%89%E6%B3%95![]() https://zh.wikipedia.org/wiki/%E5%8F%8D%E8%AD%89%E6%B3%95
https://zh.wikipedia.org/wiki/%E5%8F%8D%E8%AD%89%E6%B3%95
2.2 别名
- 反证法
- 背理法
2.3 相近概念
- 反正法是间接证明法之一
- 归谬法:反证法与归谬法相似,但归谬法不仅包括推理出矛盾结果,也包括推理出不符事实的结果或显然荒谬不可信的结果
- 归谬法(拉丁语:Reductio ad absurdum)是一种论证方式。首先归就是顺着他的意思,谬就是反驳错误的。
- 归谬法与反证法相似,差别在于反证法只限于推理出逻辑上矛盾的结果
2.4 为什么要用反证法
也就是反证法思想,想证明这个H1对,如果证明H1对有点麻烦,那么只要证明H0错误就可以了(有时候反而更简单)。比如一般情况下,证明两者相等比证明不相等更简单。
- 直接证明比较困难的时候
- 加强说服力,如果矛盾事件是错误的,那么更显得这个说法更有说服力
- ..等等
2.5 反证法的内核
2.5.1 国内的一个文章
感觉有点道理,但是实际推了下不如 维基百科的推导更好理解,可能是我学艺不精 ^ ^
百度安全验证![]() https://baijiahao.baidu.com/s?id=1779622576482381633&wfr=spider&for=pc
https://baijiahao.baidu.com/s?id=1779622576482381633&wfr=spider&for=pc


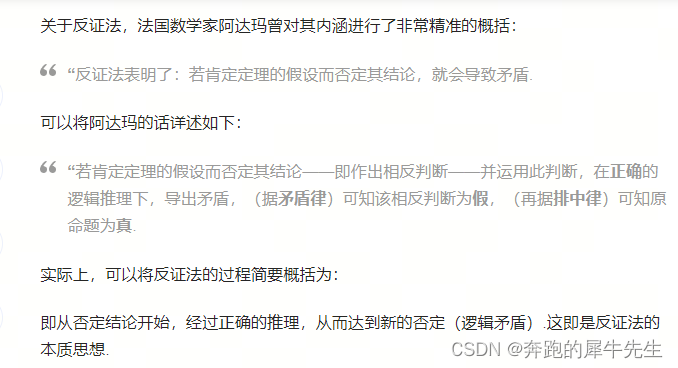
2.5.2 维基百科的反证法逻辑内核

1.7 用反证法的内核 梳理一遍假设检验的逻辑
- 我们想证明H1是对的 (但是直接证明h1有点难) →
- 我们找到H1的矛盾假设H0 →
- 我们先假设H0是对的 →从H0经过逻辑推导 →得到一个错误结论
- →根据否定后件律(我自己试了下这里用否定后见律才能推通顺,用矛盾律推导不通),如果我们推论过程符合逻辑是对的,我们从一个假设为正确的假设,推出结论却是错的,这样就前后矛盾了,因为假设真+推导正确=结论应该真,现在结论不真,只能反推假设
- →而根据排中律,如果H0是对的,那么和H0矛盾的H1,不能也是错的,因此H1是对的。
3 原假设和备择假设
3.1 原假设和备择假设
做假设检验时会设置两个假设:
- 一种叫原假设,也叫零假设,用H0表示。
- 原假设一般是统计者想要拒绝的假设。
H0 原假设的设置一般为:某个值等于多少
- 另外一种叫备择假设,用H1表示。
- 备则假设是统计者想要接受的假设。
- 也就是反证法思想,想证明这个H1对,那么只要证明H0错误就可以了.
H1 备择假设的设置一般为:某个值不等于、大于或者小于多少。
3.2 什么叫 有统计学意义? (一般= p概率很小= 拒绝原假设h0)
- 一句话:就是在统计学上来说是两者得差异是有意义的,显著的。但不一定就是实际情况 结果可能有5%或1%的可能是由误差导致
- 在统计学中,有统计学意义的结果意味着经过适当的统计分析后,某个观察到的效应不是由于偶然因素所造成的。
- 换句话说,有统计学意义的结果意味着在置信水平和误差范围内,观察到的效应真实存在,而不仅仅是由抽样误差或其他随机因素所造成的。
- 然而,需要注意的是,有统计学意义并不一定意味着观察到的效应是真实存在的。在许多情况下,我们需要进行进一步的验证和研究来确认观察到的效应是否真实存在。
3.3 有统计学意义和实际有意义不是一回事
- 比如在显著度/置信区间5%, F检验拒绝了原假设
- 但是还是有α=5%等概率并不是,有可能是随机误差造成的。也就是第一类错误。
4 两类错误
4.1 什么叫2类错误
- 但是在检验的过程中,我们通过样本数据来判断总体参数的假设是否成立,但样本是随机的,因而有可能出现小概率的错误。这种错误分两种,一种是弃真错误,另一种是取伪错误。
- 弃真错误也叫第I类错误或α错误:它是指原假设实际上是真的,但通过样本估计总体后,拒绝了原假设。明显这是错误的,我们拒绝了真实的原假设,所以叫弃真错误,这个错误的概率我们记为α。
- 取伪错误也叫第II类错误或β错误:它是指原假设实际上假的,但通过样本估计总体后,接受了原假设,这个错误的概率我们记为β。
4.2 这两类错误的计算公式
4.2.1 计算公式
- 第1类错误 / 弃真错误 / 假阳性:
- 其概率p=α
- 第2类错误/ 取伪错误 / 假阴性:
- 其概率p=β

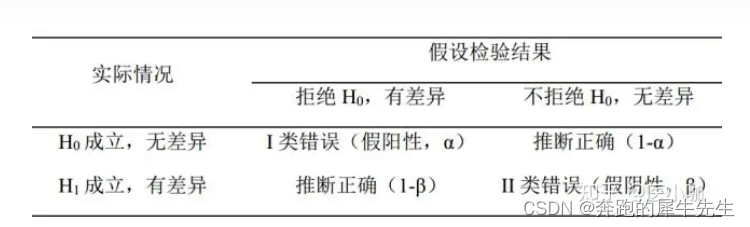
4.2.2 下面这个医学图来源
- 他们假设h0是阴性,而H1成立是阳性
- 和我画的图,横轴,纵轴是相反的
- 一般的医学的假设检验理
- h0阴性正常, 相等正常普通等标签 ( 和其他统计喜欢假设H0相等一个意思)
- h1阳性不正常
以一个研究为例,细说I类错误和II类错误! - 知乎Type I error(I类错误):犯I类错误的概率,也就是当零假设是真实的,却拒绝零假设的概率 Type II error(II类错误):犯II类错误的概率,也就是当零假设是不真实的,却接受零假设的概率 我们用一个生动形象的例…![]() https://zhuanlan.zhihu.com/p/159039017
https://zhuanlan.zhihu.com/p/159039017
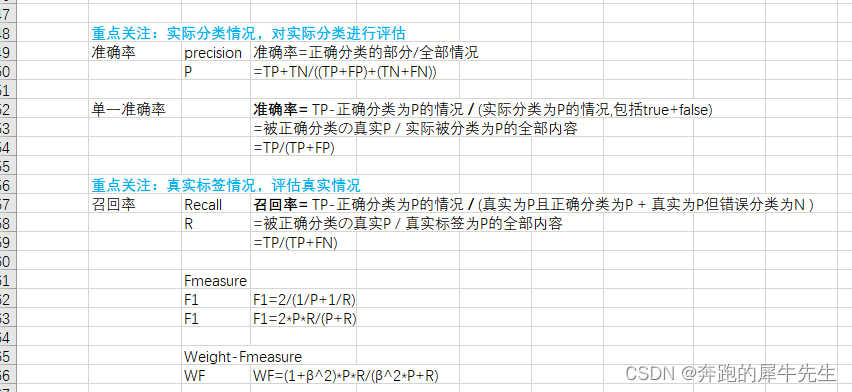
4.2.3 和机器学习理的准确率,召唤率虽然很像,但是不是一回事。

4.2.4 第1类错误和第2类错误谁更重要?
举例有这样3个假设检验
- 假设X1,X2两个样本的方差相同,实际希望方差不同。
- 假设一种药没有效果H0,实际希望有效果
- 用一个试剂去检查某人群,假设H0是阴性,实际希望是阳性
如果我们假设检验后,发现得到的概率p很小,要拒绝H0
(但开了上帝视角的我们实际发现我们的假设检验结果是错的,那会如何呢?)
- X1,X2 确实来自一个总体,但是因为假设检验,被我们认为来自不同的整体
- 这个新药实际没有效果,但是因为假设检验,被我们认为有用
- 这个人是阴性,但是因为假设检验,被我们认为是个阳性,就是假阳性
这么看起来,第1类错误,比第2类错误更危险
- 第1类错误 / 弃真错误 / 假阳性:错杀好人?
- 第2类错误/ 取伪错误 / 假阴性:放过坏人?
所以我们主要目标是减少第1类错误α的概率!如果只能选1个的话
4.2.5 两类错误不能同时消除
所以我们主要目标是减少第1类错误α的概率!是否可以同时降低第2类错误β的概率呢?不能
因为当想要犯α错误的机会变小的时候,也就是更有可能认同原假设是对的。但这就容易导致原假设本身其实是错的,却更有可能接受而犯β错误。
- type 1 error和type 2 error的概率相加不为1但存在此消彼长的关系。
- 特殊:可是在一些情况下,会共同上升或下降
- 毕竟是error,越精准,error就越少
5 如何设计H0的一些例子和思考
5.1 对H0原假设的理解
- H0 原假设,一般都是假设两者是相同分布 的这种 理想假设。
- 为什么说是理想假设,因为现实的样本里往往一定存在误差,不可能相同。因此这个H0假设是一个理想假设
- 虽然永远无法认识总体,但现实中的我们总是一厢情愿的希望,样本从总体里来是无误差的
- 理想状态:和之前说的,真实值,观测值,预测值这3种基础数据关系里的真实值一样,本质是永远无法观测到的,只存在于我们的大脑的理想国之中,所以我认为这里是需要懂一点哲学形而上的东西的。
- 一般的h0假设,总是假设2者相等,而不相等的就是h1假设
- 一般的医学的假设检验理
- h0阴性正常, 相等正常普通等标签 ( 和其他统计喜欢假设H0相等一个意思)
- h1阳性不正常
5.2 具体的例子
记住:备择假设通常才是研究者最想证明的。
举例
- 假设X1,X2两个样本的方差相同,实际希望方差不同。
- 假设一种药没有效果H0,实际希望有效果
- 用一个试剂去检查某人群,假设H0是阴性,实际希望是阳性
- 也就是
- 举例子:均匀骰子是1/6, 均匀硬币是0.5,我们认为抽样的人群能代表世界上所有人,这都是理想值(所谓的“真实值”,只存在于彼岸的真实值。即使有时候算出来刚好相等,那也应该是恰好相等而已)

从这个无罪推定的H0假设来看,也明白第1类错误更重要的原因。
6 双侧检验
双侧检验/双边检验
- 值过大过小都异常的:H1和H0相等的假设,双侧检验
- H0: 假设两者相等
- H1: 假设两者不相等。
- 很少有反过来,H0假设两者不相等的,这只能说算一个统计学惯例了
- 相等假设一般都是设计在H0内,无论是 X1=X2,甚至X1>=X2,
- 也就是说即使是单侧检验,一般都是H0 X1>=X2, 而不是X1>X2

7 左侧检验和右侧检验
7.1 右侧检验
右侧检验(相对左侧检验偏多一些,也不是一定的)
可能有一些检验是偏态的,比如F分布就一般情况下右偏。
- 上限检验
- 右侧检验关注总体参数是否明显增加
- 值大是异常的:H1大于H0,单侧检验,右侧检验
- 也就是主要关注H1, 因为统计的潜规则就是H1才是检测者想要的,那么H1是X1>X0 (对应的h0是X1<=X)就是右侧检验。
- 右侧检验,比然拒绝域也是在右边
7.2 左侧检验(下限检验)
左侧检验
- 下限检验
- 我们的预设目的是,认为H1是对的,但是反正H0是错的(这是我们的出发点,不是事实)
- 这时候我们不关注是不是更大更多,我们只关心是不是检测值会很小!越小我们就越可以拒绝H0,而接受H1
- 左侧检验关注总体参数是否明显减少/小。
- 值小是异常的:H1小于H0,单侧检验,左侧检验
- 也就是主要关注H1, 因为统计的潜规则就是H1才是检测者想要的, H1是X1<X0 (h0是X1>=X)就是左侧检验
- 左侧检验,比然拒绝域也是在左边
而单侧检验是左侧是右测,要看拒绝域的位置;而拒绝域在左侧还是右侧,要看备择假设是大于(对应右侧检验)还是小于(对应左侧检验)某个数。
8 拒绝域
- 拒绝域就是,在指定的显著度水平下,拒绝H0的区间
- 只要p落在拒绝域就拒绝H0,接受H1
8.1 双边拒绝域
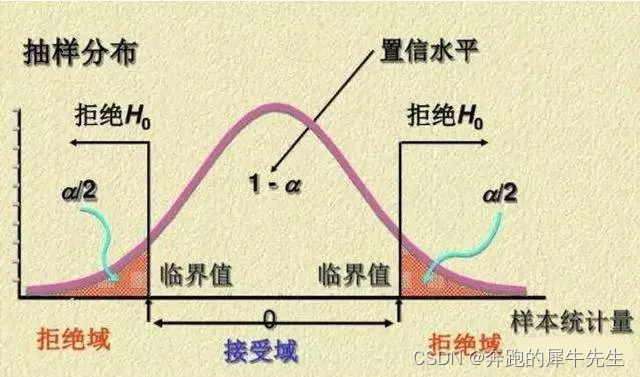
8.2 右边拒绝域
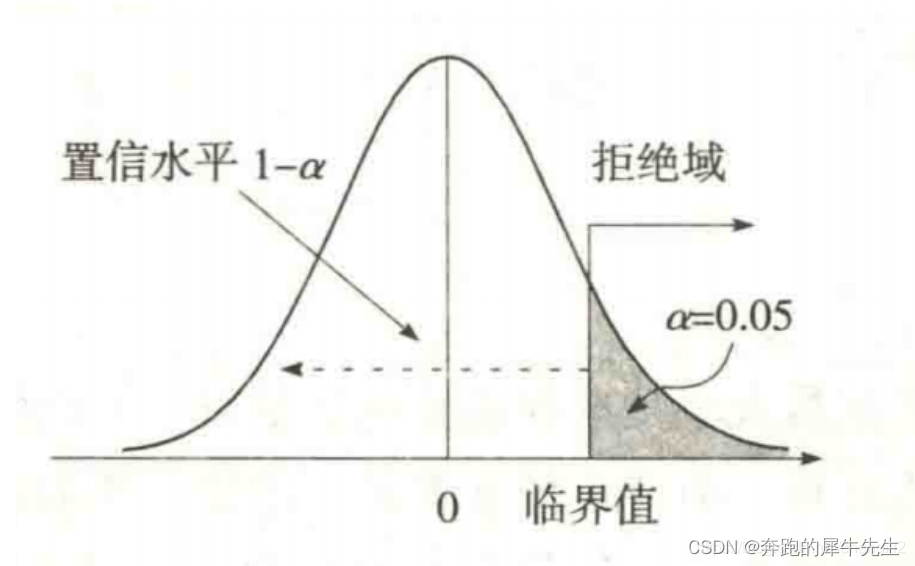
8.3 左边拒绝域
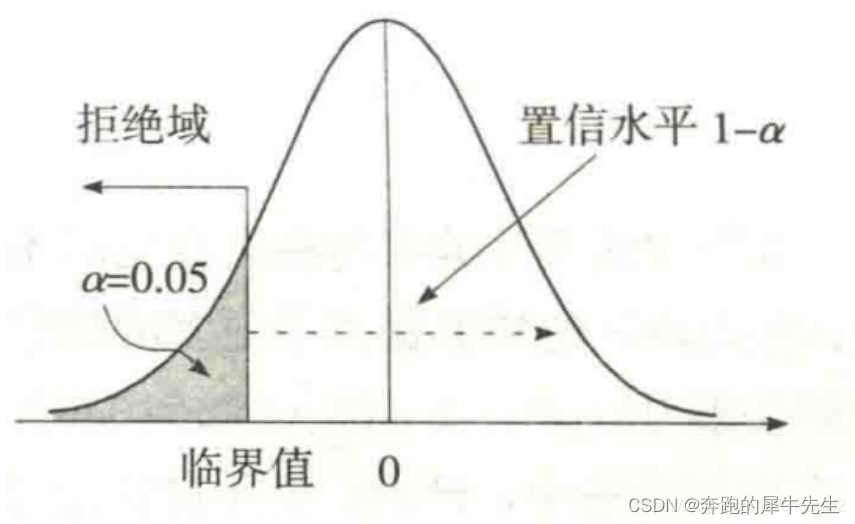
9 显著度
10 EXCEL里用函数做
11 python里做












:controls 篇)

)


![[网络安全]-059-安全大模型以及训练数据集](http://pic.xiahunao.cn/[网络安全]-059-安全大模型以及训练数据集)

