1. 背景

        Louvain算法是一种基于图数据的社区发现算法(community detection)，算法的优化目标为最大化整个数据的模块度，模块度的计算如下：

    其中m为图中边的总数量， 表示所有指向节点 i 的连边权重之和。 表示节点 i，j 之间的连边权重。有一点要搞清楚，模块度的概念不是Louvain算法发明的，而Louvain算法只是一种优化关系图模块度目标的一种实现而已。

2. 算法思想

2.1 两步迭代设计

       最开始，将每个原始节点都看成一个独立的社区，社区内的连边权重为0。

step1. 算法扫描数据中的所有节点，针对每个节点遍历该节点的所有邻居节点，衡量把该节点加入其邻居节点所在的社区所带来的模块度的收益。并选择对应最大收益的邻居节点，加入其所在的社区。这一过程化重复进行直到每一个节点的社区归属都不在发生变化。
step2. 对上述形成的社区进行折叠，把每个社区折叠成一个单点，分别计算这些新生成的“社区点”之间的连边权重，以及社区内的所有点之间的连边权重之和。用于下一轮的step1。

        该算法的最大优势就是速度很快，步骤1 的每次迭代的时间复杂度为O(N)，N为输入数据中的边的数量。步骤2 的时间复杂度为O(M + N)， M为本轮迭代中点的个数。

2.2 迭代过程

1. 假设最开始有5个点，互相之间存在一定的关系(至于什么关系，先不管)，如下：

2. 假设在经过了step1 的充分迭代之后发现节点2，应该加入到节点1 所在的社区(最开始每个点都是一个社区，而自己就是这个社区的代表)，新的社区由节点1 代表，如下：

此时节点3，4，5之间以及与节点1，2之间没有任何归属关系。

3. 此时应该执行step2，将节点1，2组合成的新社区进行折叠，折叠之后的社区看成一个单点，用节点1 来代表，如下：

        此时数据有4个节点(或4个社区)，其中一个社区包含了两个节点，而社区3，4，5都只包含一个节点，即他们自己。

4. 重新执行step1，对社区1，3，4，5进行扫描，假设在充分迭代之后节点5，4，3分别先后都加入了节点1所在的社区，如下：

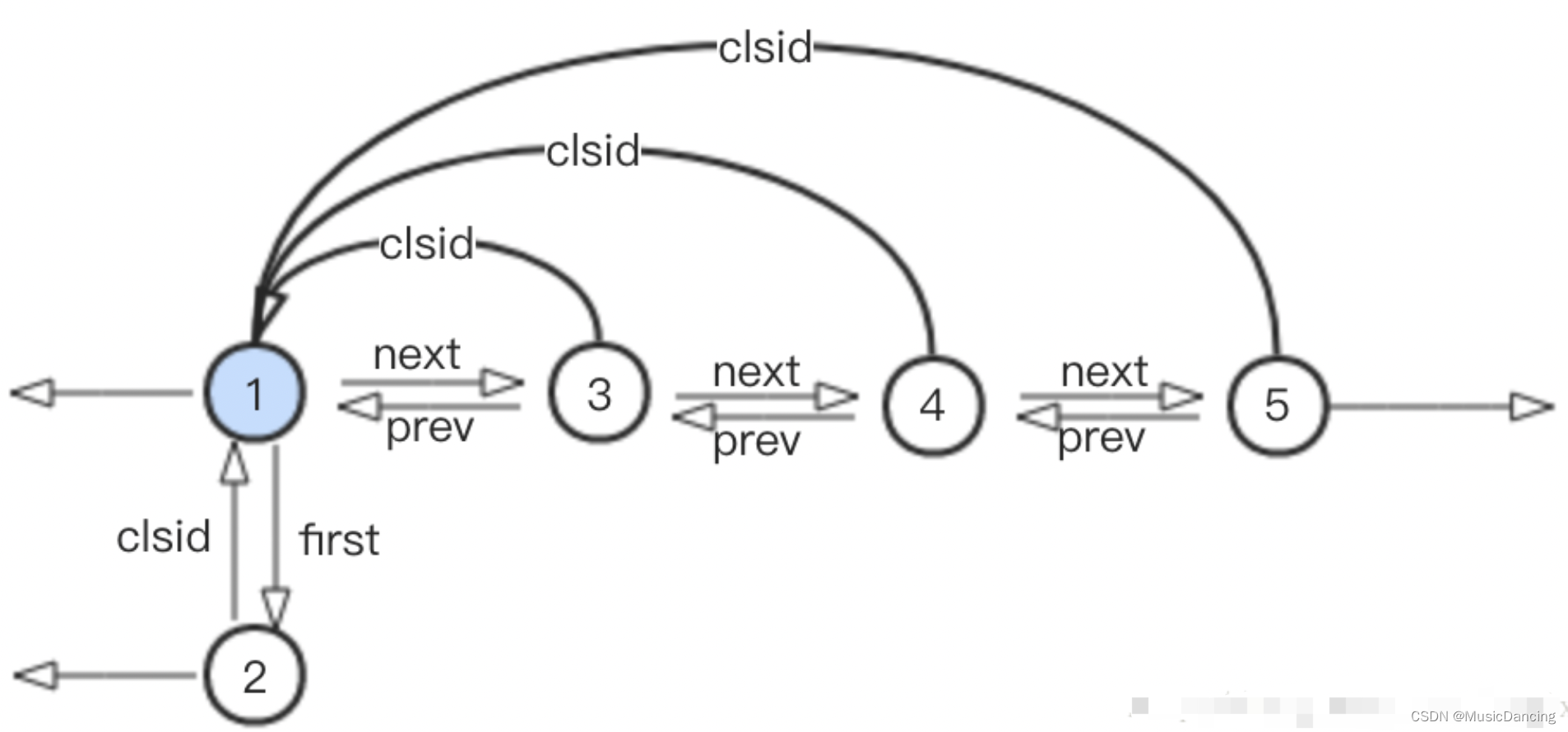
5. 进行步骤2，对新生成的社区进行折叠，新折叠而成的社区看成一个单点，由节点1代表，结构如下：

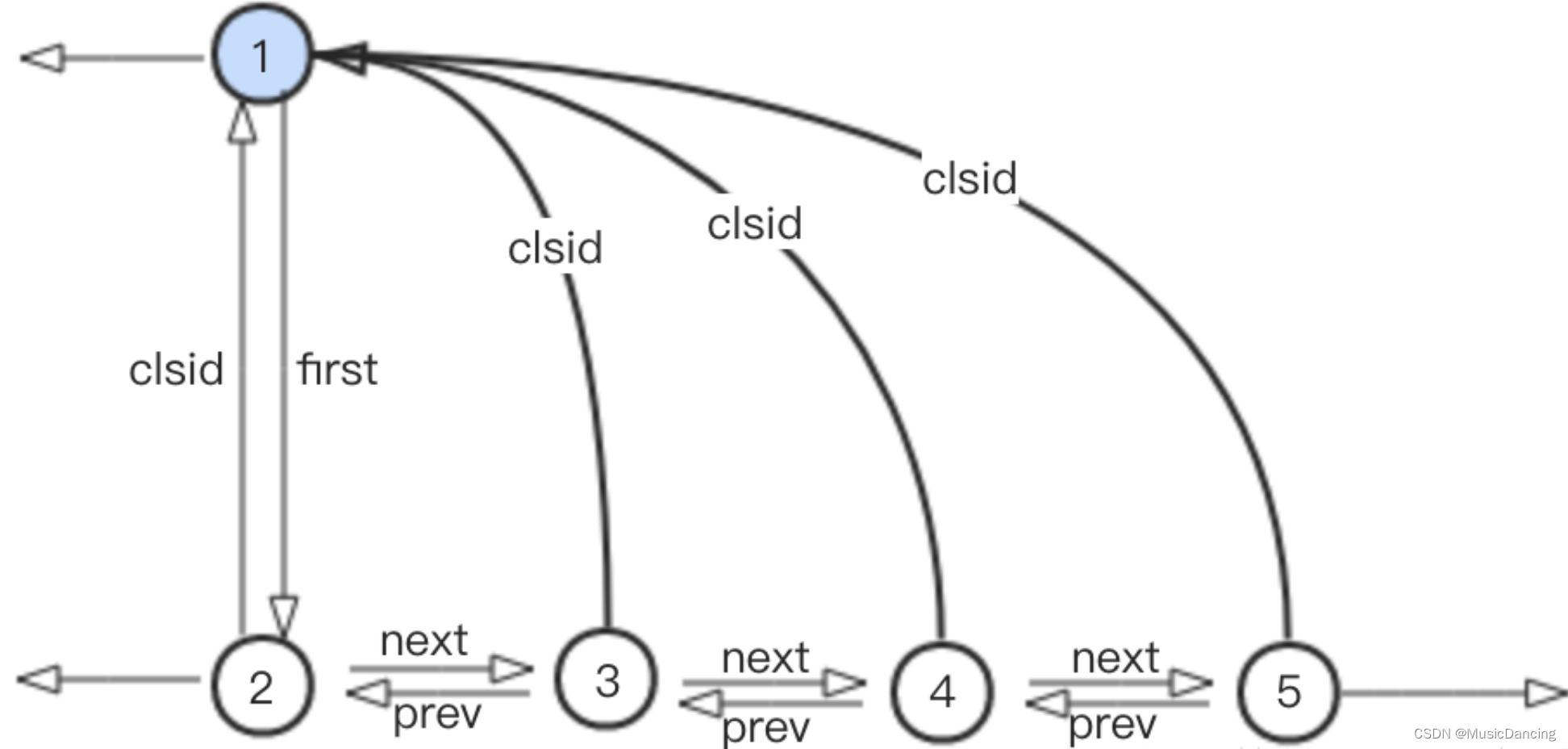
        此时由于整个数据中只剩下1个社区，即由节点1 代表的社区。再进行step1 时不会有任何一个节点的社区归属发生变化，此时也就不需要再执行step2，至此迭代结束。

3. 思考

        在团伙挖掘的过程中，介质的质量、边的构建思路、以及业务的抽象能力，比什么算法都重要，盲目的在质量不高的数据上，啥算法都没用。

4. 其他

1. 社区检测算法（Louvain、LPA 流程简介，GN算法、SLPA算法、K-L算法）；

（1）Louvain算法的算法流程

1、通过局部的更改节点社区分类来优化Modularity：先将每个节点指定到唯一的一个社区，然后按顺序将节点在这些社区间进行移动。以节点 i 为例，它有三个邻居节点 j1, j2, j3，我们分别尝试将节点 i 移动到 j1, j2, j3 所在的社区，并计算相应的 modularity 变化值，哪个变化值最大就将节点 i 移动到相应的社区中去，如果最大的变化值也为负，则不移动。

2、按照这个方法反复迭代，直到网络中任何节点的移动都不能再改善总的modularity值为止。

3、1，2两个步骤看做第一阶段。把第一阶段得到的社区视为一个新的节点。重新构造子图，两个节点之间边的权值为相应两个社区之间各边的权值的总和。

4、重复1,2,3步骤的操作，直到Modularity不再增加为止。

    (2) LPA算法的算法流程

1）为所有节点指定一个唯一的标签；

2）逐轮刷新所有节点的标签，直到达到收敛要求为止。

对于每一轮刷新，节点标签刷新的规则如下:

对于某一个节点，考察其所有邻居节点的标签，并进行统计，将出现个数最多的那个标签赋给当前节点。当个数最多的标签不唯一时，随机选一个。

2. Louvain算法是用模块度来优化，那模块度怎么改进呢（模块化密度），还有呢；

3. LPA算法从本质上来看是社区发现算法还是聚类算法（懵）；

4. 做风险社区检测，用Louvain还是LPA更合适？

5. 二叉树中的最大路径和

class Solution:def __init__(self):self.maxSum = float("-inf")def maxPathSum(self, root: TreeNode) -> int:def maxGain(node):if not node:return 0leftGain = max(maxGain(node.left),0)rightGain = max(maxGain(node.right),0)priceNewPath = node.val + leftGain + rightGainself.maxSum = max(self.maxSum, priceNewPath)return node.val + max(leftGain, rightGain)maxGain(root)return self.maxSum

6. 字典序的第K小数字

class Solution:def getSteps(self, cur: int, n: int) -> int:steps, first, last = 0, cur, curwhile first <= n:steps += min(last, n) - first + 1first *= 10last = last * 10 + 9return stepsdef findKthNumber(self, n: int, k: int) -> int:cur = 1k -= 1while k:steps = self.getSteps(cur, n)if steps <= k:k -= stepscur += 1else:cur *= 10k -= 1return cur