4.8-4.12算法刷题笔记

刷题

堆
- 1. 堆排序
- 2. 模拟堆
哈希表
- 3. 模拟散列表
- 4. 字符串哈希
DFS
- 5. 排列数字
- 6. n-皇后问题
2. BFS（队列）
- 7. 字母迷宫
- 8. 滑动谜题
3. 树与图的dfs
- 9. 树的重心
4. 树与图的bfs(最短路)
- 10. 图中点的层次( 无权最短路 )
5. 拓扑排序
- 11. 课程表
6. 朴素dijkstra算法
- 12. Dijkstra求最短路 I（邻接矩阵）
- - 普通方法：bfs
7. 堆优化版dijkstra
- 13. Dijkstra求最短路 II（邻接表）
8. Bellman-Ford算法(遍历边)
- 14. 有边数限制的最短路

堆

1. 堆排序

原题链接
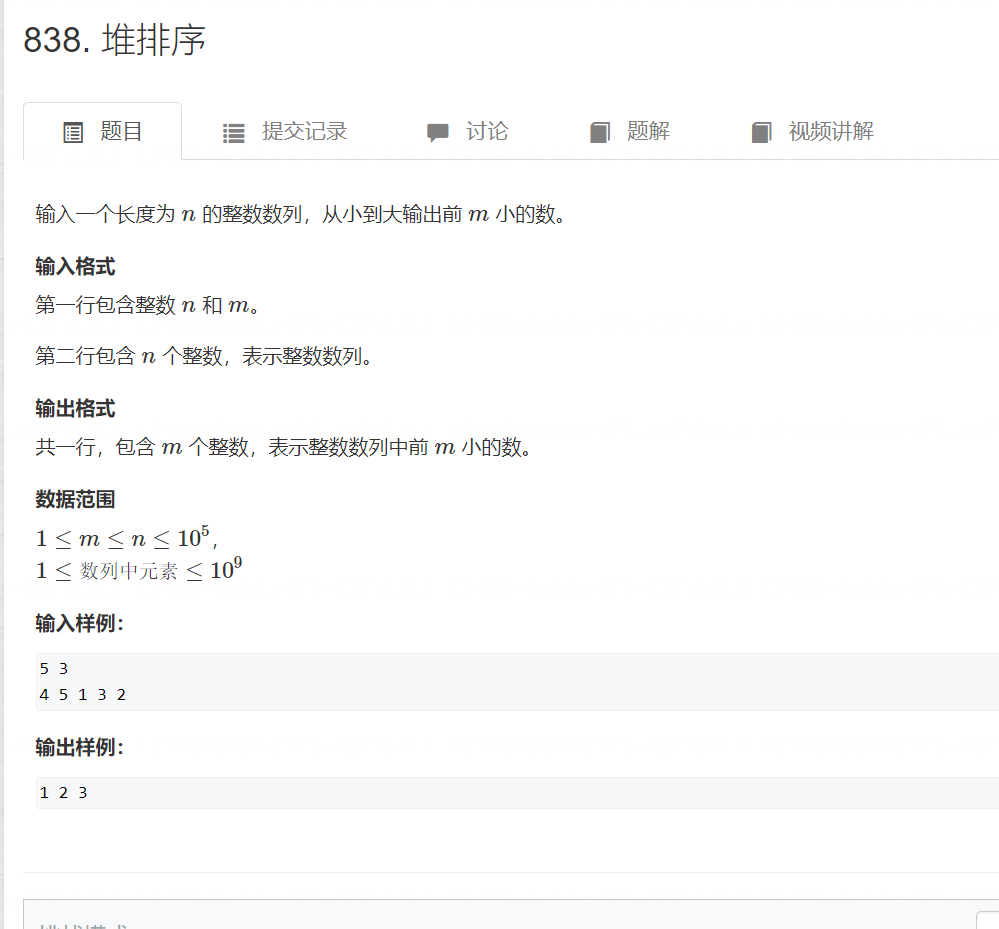
在这里插入图片描述

import java.util.*;class Main {static PriorityQueue<Integer> queue = new PriorityQueue<>();public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();for (int i = 1; i <= n; i++) {queue.add(scanner.nextInt());}for (int i = 1; i <= m; i++) {System.out.print(queue.poll() + " ");} }
}

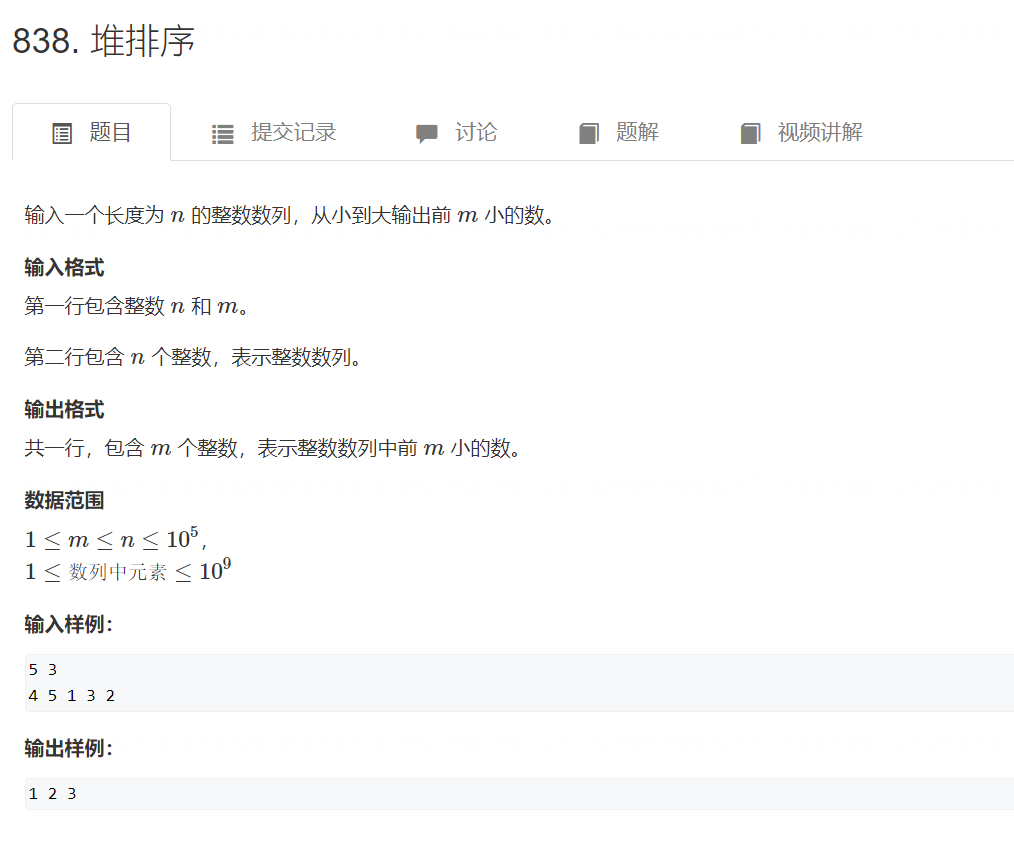
在这里插入图片描述

import java.util.Scanner;
public class Main{static int N = 100010;static int[] h = new int[N];static int size;//交换函数public static void swap(int x,int y){int temp = h[x];h[x] = h[y];h[y] = temp;}//堆函数核心函数，堆排序函数,传入的参数u是下标public static void down(int u){int t = u; // t用来分身变量//u的左分支下标小于size说明该数存在,然后如果这个数小于t，则让左下标赋值给t,即u的分身 if(u * 2 <= size && h[u * 2] < h[t]) t = u * 2; //u的右分支下标小于size说明该数存在，然后如果这个数小于t，因为可能上面的if语句会重置t，则判断是不是小于新或旧t,//如果小于t的话，就让右下标赋值给t ,即u的分身。if(u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;//如果u不等于t,说明左或者右下标有比较小的值赋值给t了，分身变了if(u != t){//就让u跟t这两个数交换一下位置，让小的数替代u的位置swap(u,t);//然后继续递归t下标小的位置down(t);}}public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();for(int i = 1 ; i <= n ; i ++ ) h[i] = scan.nextInt(); //首先将所有数先存入数组中size = n;//长度为n//从n/2的位置开始将数组中的值插入堆中//堆结构是一个完全二叉树，所有有分支的数等于没有分支的数，即最后一排的数量等于上面所有的数//最下面一排没有分支的数不用参与插入，所以从n/2开始进行插入for(int i = n/2 ; i >= 0; --i ) down(i);//就是让他进行向下排序处理 while(m -- > 0){//输出前m小的m个元素System.out.print(h[1] + " "); //每一次输出头节点//因为是数组，删除第一个数复杂，删除最后一个元素比较简单//所以就将最后一个元素将第一个元素覆盖掉，然后删除掉最后一个元素h[1] = h[size--];//然后进行堆排序，对第一个元素进行处理down(1);}}
}

2. 模拟堆

原题链接

在这里插入图片描述

import java.util.Scanner;
public class Main{static int N = 100010,size,m;static int[] h = new int[N];static int[] hp = new int[N];//自身被映射数组static int[] ph = new int[N];//映射数组public static void swap(int[] a,int x,int y){int temp = a[x];a[x] = a[y];a[y] = temp;}public static void head_swap(int x,int y){//这里因为映射数组跟被映射数组是互相指向对方,如果有两个数更换位置，映射下标也要进行更换//ph的下标指向是按顺序插入的下标，hp所对应的值是ph的按顺序的下标，用这两个属性进行交换swap(ph,hp[x],hp[y]);//因为按照顺序插入ph到指向交换了，对应指向ph的hp也要进行交换swap(hp,x,y);//最后两个值进行交换swap(h,x,y);}public static void down(int x){int t = x;//x的分身//判断一下左下标是不是存在//判断一下左下标的值是不是比我t的值小 。那么就将左下标的值赋予t；否则不变if(x * 2 <= size && h[x * 2] < h[t]) t = x * 2;//判断一下右下标的值是不是比我t的值小。那么就将右下标的值赋予t，否则不变if(x *2 + 1 <= size && h[x * 2 + 1] < h[t]) t = x * 2 + 1;if(t != x){//如果x不等于他的分身head_swap(x,t);//那就进行交换顺序down(t);//然后一直向下进行操作}}public static void up(int x){//向上操作，判断一下根节点还不是存在//看一下根节点是不是比我左分支或者右分支的值大，大的话就进行交换while(x / 2 > 0 && h[x / 2] > h[x]){head_swap(x,x/2);x = x / 2;//相当于一直up}}public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();size = 0;//size是原数组的下标m = 0;//m是映射数组的下标while(n -- > 0){String s = scan.next();if(s.equals("I")){//插入操作int x= scan.nextInt();size ++;m ++;//插入一个数两个数组的下标都加上1；ph[m] = size;hp[size] = m;//ph与hp数组是映射关系h[size] = x;//将数插入到堆中最后位置up(size);//然后up，往上面排序一遍}else if(s.equals("PM")){ //输出当前集合中的最小值System.out.println(h[1]);}else if(s.equals("DM")){//删除当前集合中的最小值//因为需要用到映射数组与被映射数组,因为需要找到k的位置在哪里，需要让映射的顺序，//因为如果用size，size是会随时改变的，不是按顺序的，因为会被up或者down顺序会被修改head_swap(1,size);//将最后一个数替换掉第一个最小值元素，然后数量减1，size--size--;down(1);//插入之后进行向下操作，因为可能不符合小根堆}else if(s.equals("D")){//删除当前集合中第k个插入得数int k = scan.nextInt();k = ph[k];//ph[k] 是一步一步插入映射的下标，不会乱序，head_swap(k,size);//然后将k与最后一个元素进行交换，然后长度减1，size--size--;up(k);//进行排序一遍，为了省代码量，up一遍down一遍。因为只会执行其中一个down(k);}else{int k = scan.nextInt();int x = scan.nextInt();k = ph[k];//ph[k] 是一步一步插入映射的下标，顺序是按照插入时候的顺序h[k] = x;//然后将第k为数修改为数xup(k);//up一遍，down一遍down(k);}}}
}

哈希表

(1) 拉链法int h[N], e[N], ne[N], idx;// 向哈希表中插入一个数void insert(int x){int k = (x % N + N) % N;e[idx] = x;ne[idx] = h[k];h[k] = idx ++ ;}// 在哈希表中查询某个数是否存在bool find(int x){int k = (x % N + N) % N;for (int i = h[k]; i != -1; i = ne[i])if (e[i] == x)return true;return false;}(2) 开放寻址法int h[N];// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置int find(int x){int t = (x % N + N) % N;while (h[t] != null && h[t] != x){t ++ ;if (t == N) t = 0;}return t;}

3. 模拟散列表

原题链接

在这里插入图片描述
拉链法代码（链表）

N取大于范围的第一个质数
k = (x % N + N) % N; （%N 为了避免超级大的值 + N 为了避免出现负数再%N为了正数+N超出范围）
memset(h, -1, sizeof h);

import java.util.Scanner;
public class Main{static int N = 100003,idx;static int[] h = new int[N];static int[] e = new int[N];static int[] ne = new int[N];public static void add(int x){int k = (x % N + N) % N;e[idx] = x;ne[idx] = h[k];h[k] = idx ++ ;}public static boolean find(int x){int k = (x % N + N) % N;for(int i = h[k];i != -1;i = ne[i]){if(e[i] == x){return true;}    }return false;}public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();idx = 0;for(int i = 0 ; i < N ; i++ ){h[i] = -1;}while(n -- > 0){String x = scan.next();if(x.equals("I")){int a = scan.nextInt();add(a);}else{int b = scan.nextInt();if(find(b)) System.out.println("Yes");else System.out.println("No");}}}
}

开放寻址法代码（有空位就存，空位用null=0x3f3f3f3f）

大于2倍的第一个质数

#include <cstring>
#include <iostream>using namespace std;//开放寻址法一般开 数据范围的 2~3倍, 这样大概率就没有冲突了
const int N = 2e5 + 3;        //大于数据范围的第一个质数
const int null = 0x3f3f3f3f;  //规定空指针为 null 0x3f3f3f3fint h[N];int find(int x) {int t = (x % N + N) % N;while (h[t] != null && h[t] != x) {t++;if (t == N) {t = 0;}}return t;  //如果这个位置是空的, 则返回的是他应该存储的位置
}int n;int main() {cin >> n;memset(h, 0x3f, sizeof h);  //规定空指针为 0x3f3f3f3fwhile (n--) {string op;int x;cin >> op >> x;if (op == "I") {h[find(x)] = x;} else {if (h[find(x)] == null) {puts("No");} else {puts("Yes");}}}return 0;
}

4. 字符串哈希

原题链接

把一段字符串转成一段数字，便可以直接比较相等
怎么转？进制大于26
样例没找全 p[r-l+1] 这个点没找到

import java.util.Scanner ;
public class Main{//开的是long类型数组，本来是需要进行前缀hash求完之后需要进行模2的64次方来防止相同的冲突，可能超过我们给的数组大小static int N = 100010,P = 131;//p是进制数，惊艳值static long[] h = new long[N];//这是存放hash前缀值得数组static long[] p = new long[N];//这是存放p的n次方的数组public static long get(int l,int r){//这里是将运用了一点前缀和公式的方式进行计算//求l-r区间的hash值，就要用h[r] - h[l-1],因为两者位数不用需要让h[l-1]向左边移到跟h[r]对齐//就比如求1234的3-4区间位，1234 - 12,12左移然后就让12*10^(4-3+1)=12*10^2=1200,然后1234-1200 = 34,这样进行计算出来//然后本题是p进制，所以需要将上面公式中的10换成p就行了//h[0] = 0//h[1] = h[i-1] * P + str[1] = 0*P+a = a//h[2] = a * P + b//h[3] = (a*P+b)*P+c = a*p[2]+b*P+c//h[4] = (a*p[2]+b*P+c)*P+d = a*p[3]+b*p[2]+c*P+d//比如abcd求3-4区间位，就是让h[d]-h[b]，h[b]位数不用需要向左移对齐h[d],//h[2]*P^(4-3+1)=(a*P+b)*P^2 = a*P^3+b*P^2//然后就让h[d] - h[b]求出34区间值,(a*p[3]+b*p[2]+c*P+d) - (a*P^3+b*P^2) = c*P+dreturn h[r] - h[l-1]*p[r-l+1];}public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();String s = scan.next();p[0] = 1;//这个是p的0次方的值，需要单独写出来，非常重要for(int i = 1 ; i <= n ; i++ ){p[i] = p[i-1] * P;//这里对应每一个下标对应对应P的多少次方h[i] = h[i-1] * P + s.charAt(i-1);//这里是公式，预处理前缀哈希的值，因为是P进制，所以中间乘的是P}while(m -- > 0){int l1 = scan.nextInt();int r1 = scan.nextInt();int l2 = scan.nextInt();int r2 = scan.nextInt();//判断两个区间是不是相同,用get的方法返回值一样说明区间的hash值是一样的if(get(l1,r1) == get(l2,r2)) System.out.println("Yes");else System.out.println("No");}}
}

DFS

5. 排列数字

每次遍历dfs参数是遍历的坑位
力扣链接
acwing链接

#include<iostream>
using namespace std;
const int N = 10;
int path[N];//保存序列
int state[N];//数字是否被用过
int n;
void dfs(int u)//u表示的是 第几个坑位
{if(u > n)//数字填完了，输出{for(int i = 1; i <= n; i++)//输出方案cout << path[i] << " ";cout << endl;}for(int i = 1; i <= n; i++)//空位上可以选择的数字为:1 ~ n{if(!state[i])//如果数字 i 没有被用过{path[u] = i;//放入空位state[i] = 1;//数字被用，修改状态dfs(u + 1);//填下一个位state[i] = 0;//回溯，取出 i}}
}int main()
{cin >> n;dfs(1);
}

6. n-皇后问题

力扣链接
acwing链接

class Solution {public List<List<String>> solveNQueens(int n) {List<List<String>> solutions = new ArrayList<List<String>>();int[] queens = new int[n];Arrays.fill(queens, -1);Set<Integer> columns = new HashSet<Integer>();Set<Integer> diagonals1 = new HashSet<Integer>();Set<Integer> diagonals2 = new HashSet<Integer>();backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);return solutions;}public void backtrack(List<List<String>> solutions, int[] queens, int n, int row, Set<Integer> columns, Set<Integer> diagonals1, Set<Integer> diagonals2) {if (row == n) {List<String> board = generateBoard(queens, n);solutions.add(board);} else {for (int i = 0; i < n; i++) {if (columns.contains(i)) {continue;}int diagonal1 = row - i;if (diagonals1.contains(diagonal1)) {continue;}int diagonal2 = row + i;if (diagonals2.contains(diagonal2)) {continue;}queens[row] = i;columns.add(i);diagonals1.add(diagonal1);diagonals2.add(diagonal2);backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);queens[row] = -1;columns.remove(i);diagonals1.remove(diagonal1);diagonals2.remove(diagonal2);}}}public List<String> generateBoard(int[] queens, int n) {List<String> board = new ArrayList<String>();for (int i = 0; i < n; i++) {char[] row = new char[n];Arrays.fill(row, '.');row[queens[i]] = 'Q';board.add(new String(row));}return board;}
}

方法 1. 按行遍历（过程中有回溯、剪枝）

思想：

每次递归中，遍历一行的元素，如果可以放皇后，就递归到下一行，下一行中不行了，就返回来，回溯，

//cpp
#include <iostream>
using namespace std;const int N = 11;char q[N][N];//存储棋盘
bool dg[N * 2], udg[N * 2], cor[N];
//点对应的两个斜线以及列上是否有皇后int n;void dfs(int r)
{if(r == n)//放满了棋盘，输出棋盘{for(int i = 0; i < n; i++){for(int j = 0; j < n; j++)cout << q[i][j];cout << endl;}cout << endl;return;}for(int i = 0; i < n; i++)//第 r 行，第 i 列 是否放皇后{if(!cor[i] && !dg[i + r] && !udg[n - i + r])//不冲突，放皇后{q[r][i] = 'Q';cor[i] = dg[i + r] = udg[n - i + r] = 1;//对应的 列， 斜线 状态改变dfs(r + 1);//处理下一行cor[i] = dg[i + r] = udg[n - i + r] = 0;//恢复现场q[r][i] = '.';}}
}int main()
{cin >> n;for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )q[i][j] = '.';dfs(0);return 0;
}

方法2. 按每个元素遍历（没有减枝）

// 不同搜索顺序 时间复杂度不同  所以搜索顺序很重要！
#include <iostream>
using namespace std;
const int N = 20;int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N]; 
// 因为是一个个搜索，所以加了row// s表示已经放上去的皇后个数
void dfs(int x, int y, int s)
{// 处理超出边界的情况if (y == n) y = 0, x ++ ;if (x == n) { // x==n说明已经枚举完n^2个位置了if (s == n) { // s==n说明成功放上去了n个皇后for (int i = 0; i < n; i ++ ) puts(g[i]);puts("");}return;}//和上面按行遍历的差别就是，这里没有循环// 分支1：放皇后if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]) {g[x][y] = 'Q';row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;dfs(x, y + 1, s + 1);row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;g[x][y] = '.';}// 分支2：不放皇后dfs(x, y + 1, s);
}int main() {cin >> n;for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )g[i][j] = '.';dfs(0, 0, 0);return 0;
}

2. BFS（队列）

7. 字母迷宫

class Solution {public boolean wordPuzzle(char[][] grid, String word) {int h = grid.length, w = grid[0].length;boolean[][] visited = new boolean[h][w];for (int i = 0; i < h; i++) {for (int j = 0; j < w; j++) {boolean flag = exist(grid, visited, i, j, word, 0);if (flag) {return true;}}}return false;}public boolean exist(char[][] grid, boolean[][] visited, int i, int j, String s, int k) {if (grid[i][j] != s.charAt(k)) {return false;} else if (k == s.length() - 1) {return true;}visited[i][j] = true;int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};boolean result = false;for (int[] dir : directions) {int newi = i + dir[0], newj = j + dir[1];if (newi >= 0 && newi < grid.length && newj >= 0 && newj < grid[0].length) {if (!visited[newi][newj]) {boolean flag = exist(grid, visited, newi, newj, s, k + 1);if (flag) {result = true;break;}}}}visited[i][j] = false;return result;}
}

原题链接
原题链接

class Solution {public boolean wordPuzzle(char[][] grid, String word) {int h = grid.length, w = grid[0].length;boolean[][] visited = new boolean[h][w];for (int i = 0; i < h; i++) {for (int j = 0; j < w; j++) {boolean flag = exist(grid, visited, i, j, word, 0);if (flag) {return true;}}}return false;}public boolean exist(char[][] grid, boolean[][] visited, int i, int j, String s, int k) {if (grid[i][j] != s.charAt(k)) {return false;} else if (k == s.length() - 1) {return true;}visited[i][j] = true;int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};boolean result = false;for (int[] dir : directions) {int newi = i + dir[0], newj = j + dir[1];if (newi >= 0 && newi < grid.length && newj >= 0 && newj < grid[0].length) {if (!visited[newi][newj]) {boolean flag = exist(grid, visited, newi, newj, s, k + 1);if (flag) {result = true;break;}}}}visited[i][j] = false;return result;}
}

#include<iostream>
#include<cstring>using namespace std;int n,m;
int p[110][110];
int d[110][110];
int dx[4] = {-1,0,1,0};
int dy[4] = {0,-1,0,1};pair<int,int> q[110*110];
int hh,tt=-1;void bfs()
{q[++tt] = {1,1};p[1][1] = 1;d[1][1] = 0;while(hh<=tt){pair<int,int> item = q[hh++];for(int i = 0; i < 4; i++){int x = item.first;int y = item.second;//cout << x << ' ' << y << endl;if(p[x+dx[i]][y+dy[i]]!=1 && x+dx[i]<=n && x+dx[i] > 0 && y+dy[i] <=m && y+dy[i] >0){d[x+dx[i]][y+dy[i]] = d[x][y] + 1;q[++tt] = {x+dx[i],y+dy[i]};p[x+dx[i]][y+dy[i]] = 1;}}}
}int main()
{cin >> n >> m;for(int i = 1; i<=n; i++){for(int j = 1; j<=m; j++)cin >> p[i][j];}bfs();cout << d[n][m];return 0;
}

8. 滑动谜题

力扣链接
acwing链接


class Solution {public int slidingPuzzle(int[][] board) {int m = 2, n = 3;StringBuilder sb = new StringBuilder();String target = "123450";// 将 2x3 的数组转化成字符串作为 BFS 的起点for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {sb.append(board[i][j]);}}String start = sb.toString();// 记录一维字符串的相邻索引int[][] neighbor = new int[][]{{1, 3},{0, 4, 2},{1, 5},{0, 4},{3, 1, 5},{4, 2}};/******* BFS 算法框架开始 *******/Queue<String> q = new LinkedList<>();HashSet<String> visited = new HashSet<>();// 从起点开始 BFS 搜索q.offer(start);visited.add(start);int step = 0;while (!q.isEmpty()) {int sz = q.size();for (int i = 0; i < sz; i++) {String cur = q.poll();// 判断是否达到目标局面if (target.equals(cur)) {return step;}// 找到数字 0 的索引int idx = 0;for (; cur.charAt(idx) != '0'; idx++) ;// 将数字 0 和相邻的数字交换位置for (int adj : neighbor[idx]) {String new_board = swap(cur.toCharArray(), adj, idx);// 防止走回头路if (!visited.contains(new_board)) {q.offer(new_board);visited.add(new_board);}}}step++;}/******* BFS 算法框架结束 *******/return -1;}private String swap(char[] chars, int i, int j) {char temp = chars[i];chars[i] = chars[j];chars[j] = temp;return new String(chars);}
}

#include<iostream>
#include<unordered_map>
#include<cstring>
#include<queue>using namespace std;int bfs(string s)
{queue<string> q;q.push(s);int dx[4] = { 1,0,-1,0 },dy[4] = { 0,-1,0,1 };unordered_map<string, int> d;d[s] = 0;while (!q.empty()){string f = q.front();q.pop();if (f == "12345678x")return d[f];int df = d[f];int k = f.find("x");int x = k / 3;int y = k % 3;for (int i = 0; i < 4; i++){if (x + dx[i] <= 2 && x + dx[i] >= 0 && y + dy[i] <= 2 && y + dy[i] >= 0){swap(f[k], f[(x + dx[i]) * 3 + y + dy[i]]);if (!d.count(f)){d[f] = df + 1;q.push(f);}swap(f[k], f[(x + dx[i]) * 3 + y + dy[i]]);}}}return -1;
}int main()
{char ch;string s;for (int i = 0; i < 9; i++){cin >> ch;s += ch;}cout << bfs(s);return 0;
}

3. 树与图的dfs

9. 树的重心

在这里插入图片描述

原题链接

void add(int a,int b)
{e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}

遍历过的点标记一下，不再遍历，因为无向图可能往回遍历

import java.util.*;
public class Main{static int N = 100010,M = N * 2,idx,n;static int[] h = new int[N];static int[] e = new int[M];//存的是双倍，所以是Mstatic int[] ne = new int[M];//存的是双倍，所以是Mstatic boolean[] st = new boolean[N];static int ans = N; //一开始将最大值赋值成N,最大了/**** 邻接表，存储方法* 邻接表不用管执行顺序，只需要知道每个节点能够执行到每个多少个节点就行* 比如案例中4 3 , 4 6 ,头结点4插入两个节点3和6,所以执行到4就能够执行3和6,* 固定的，邻接表就是这样子的***/public static void add(int a,int b){e[idx] = b;ne[idx] = h[a];h[a] = idx++;}//返回的是当前子树的数量,比如1下面的所有数量包括自己就是9public static int dfs(int u){int res = 0;//连通块中的最大值这个其实就是ans，到时候跟ans比较大小，小的话就赋值给ans的st[u] = true;//将这个删除的点标记，下次不在遍历int sum = 1;//将删除的点也算上是初始值就是1;到时候有利于求n-sum;//单链表遍历for(int i = h[u];i != -1 ; i = ne[i]){int j = e[i];//然后将每一个的指向的点用变量表示出来if(!st[j]){ //然后如果是没用过，没被标记过的，就可以执行int s = dfs(j);//然后递归他的邻接表上面所有能够抵达的点//然后返回的数量是他所删除的点下面的连通块的大小res = Math.max(res,s); //然后和res比较一下大小，谁大谁就是最大连通块sum += s; //这里是将每递归一个点，就增加一个返回的s，就可以将这个值作为返回值成为最大连通块}}/**** 因为邻接表表中只是往下面执行，删除的点的上面的连通块可能是最大的连通块，* 所以需要用总数减去我们下面所统计出来的最大的连通块* 然后将最大的连通块的值赋值给res* **/res = Math.max(res,n-sum); //然后将每个次的最大值进行比较，留下最小的最大值ans = Math.min(res,ans);return sum;}    public static void main(String[] ags){Scanner scan = new Scanner(System.in);n = scan.nextInt();//这里是将每一个头节点都赋值成-1for(int i = 1 ; i < N ; i++ ){h[i] = -1;}//案例输入输出for(int i = 0 ; i < n - 1 ; i ++){int a = scan.nextInt();int b = scan.nextInt();//因为是无向边，所以就两个数同时指向对方add(a,b);add(b,a);}dfs(1);//从1开始//最后输出的是最小的最大值System.out.println(ans);}
}

4. 树与图的bfs(最短路)

在这里插入图片描述

10. 图中点的层次( 无权最短路 )

原题链接
原题链接

import java.util.Scanner;
public class Main{static int N = 100010,n,m,idx,hh,tt;static int[] h = new int[N],e = new int[N],ne = new int[N];static int[] d = new int[N],q = new int[N];//这个是单链表的模板public static void add(int a,int b){e[idx] = b;ne[idx] = h[a];h[a] = idx++;}public static int bfs(){hh = 0 ; tt = -1;d[1] = 0; // 第一个点是距离为0q[++tt] = 1; //然后将第一个点加进去//如果队列不是空的while(hh <= tt){int t = q[hh++]; //取出队头//然后遍历一下单链表for(int i = h[t] ; i != -1 ; i = ne[i]){int s = e[i]; //然后这个点用一个变量表示if(d[s] == -1){ //如果这个点是没走过的d[s] = d[t] + 1; //然后将这个点距离加上1q[++tt] = s;//然后将第二步的点加入到队尾中}}}return d[n]; //最后返回1到n的最短距离d}public static void main(String[] args){Scanner scan = new Scanner(System.in);n = scan.nextInt();m = scan.nextInt();//这里需要将距离跟头结点都赋值成-1for(int i = 1 ; i < N ; i++){h[i] = -1;d[i] = -1; }for(int i = 0 ; i < m ; i ++ ){int a = scan.nextInt();int b = scan.nextInt();add(a,b);}System.out.println(bfs());}
}

5. 拓扑排序

11. 课程表

力扣链接
acwing链接

class Solution {private static final int N = 5001;private static int[] e;private static int[] ne;private static int[] h;private static int[] cnt;private static int idx;private static void add(int a,int b) {e[idx] = b;ne[idx] = h[a];cnt[b]++;h[a] = idx++;}public boolean canFinish(int numCourses, int[][] prerequisites) {e = new int[N];ne = new int[N];h = new int[N];cnt = new int[N];idx = 0;Arrays.fill(h,-1);for (int[] temp : prerequisites) {add(temp[1],temp[0]);}Queue<Integer> queue = new LinkedList<>();for (int i = 0; i < numCourses; i++) {if (cnt[i] == 0) {queue.add(i);}}int sum = 0;while (!queue.isEmpty()) {int r = queue.remove();sum++;for (int i = h[r]; i != -1; i = ne[i]) {int j = e[i];cnt[j]--;if (cnt[j] == 0) {queue.add(j);}}}if (sum == numCourses) {return true;} else {return false;}}
}

import java.util.*;
public class Main{static int N =  100010,n,m,hh,tt,idx;static int[] e = new int[N],ne = new int[N],h = new int[N];static int[] q = new int[N];static int[] d = new int[N];public static void add(int a,int b){e[idx] = b;ne[idx] = h[a];h[a] = idx++;}public static boolean bfs(){hh = 0 ; tt = -1;for(int i = 1 ; i <= n ; i ++ ){ if(d[i] == 0){     //首先将所有入度为0的点全部插入q队列中q[++tt] = i;}}while(hh <= tt){int t = q[hh++]; //拿出队头for(int i = h[t] ; i != -1; i = ne[i]){ //遍历一下队列中所有的边int s = e[i]; //然后将这个边拿出来d[s] -- ; //将这个边的入度数减1if(d[s] == 0){q[++tt] = s; //如果减完之后s的入度数为0；就将他插入队列中}       }}return tt == n - 1; //最后返回，如果队列中的tt等于n-1个数，说明就是正确的的}public static void main(String[] args){Scanner scan = new Scanner(System.in);n = scan.nextInt();m = scan.nextInt();for(int i = 0 ; i < N ; i ++ ){h[i] = -1; }while(m -- > 0){int a = scan.nextInt();int b = scan.nextInt();add(a,b);d[b] ++;}if(bfs()){//队列刚好队头删除的点就是我们的拓扑序列，因为我们只是将hh往后面移动，但是它具体前面的值还在，直接输出就行for(int i = 0 ; i < n; i ++ ){ System.out.print(q[i] + " ");}}else{System.out.println("-1");}}
}

#include<iostream>
#include<cstring>
#include<queue>using namespace std;const int N = 1e5+10;bool st[N];
int e[N],ne[N],idx,h[N];
int b[N];//每个节点的入读int n,k;  queue<int> q,ans;void bfs()
{while(q.size()){int f = q.front();q.pop();for(int i = h[f]; i != -1; i = ne[i]){b[e[i]]--;if(b[e[i]]==0){ans.push(e[i]);q.push(e[i]);}}}}void add(int a,int b)
{e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}int main()
{ memset(h,-1,sizeof h);cin >> n >> k;for(int i = 1; i <= k; i++){int a,bb;cin >> a >> bb;add(a,bb);b[bb]++;}for(int i = 1; i <= n; i++){if(b[i]==0){//cout << i << endl;q.push(i);ans.push(i);}}bfs();if(ans.size()!=n){cout << -1;return 0;}//cout << ans.size() << endl;while(ans.size()){cout << ans.front() << ' ';ans.pop();}return 0;
}

6. 朴素dijkstra算法

12. Dijkstra求最短路 I（邻接矩阵）

在这里插入图片描述

原题链接
刷题总结

稀疏矩阵和疏密矩阵（疏密矩阵可以用邻接矩阵存储方式）
邻接矩阵直接就可以存储边距离了
d存储到1节点的距离

二刷总结

dijk就是两步：1. 在dist里选出最小值 2.遍历dist更新
如何选(如下)

int t = -1;
for (int j = 1; j <= n; j ++ )if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;


import java.util.*;
public class Main{static int N = 510,n,m, max = 0x3f3f3f3f;static int[][] g = new int[N][N];//存每个点之间的距离static int[] dist = new int[N];//存每个点到起点之间的距离static boolean[] st = new boolean[N];//存已经确定了最短距离的点public static int dijkstra(){Arrays.fill(dist,max);//将dist数组一开始赋值成较大的数dist[1] = 0; //首先第一个点是零//从0开始,遍历n次，一次可以确定一个最小值for(int i = 0 ; i < n ; i ++ ){ int t = -1; //t这个变量,准备来说就是转折用的for(int j = 1 ; j <= n ; j ++ ){/**** 因为数字是大于1的，所以从1开始遍历寻找每个数* 如果s集合中没有这个数* 并且t == -1，表示刚开始 或者 后面的数比我心找的数距离起点的距离短* 然后将j 的值赋值给 t***/if(!st[j] && (t == -1 || dist[j] < dist[t])){t = j; }}st[t] = true;//表示这个数是已经找到了确定了最短距离的点//用已经确认的最短距离的点来更新后面的点//就是用1到t的距离加上t到j的距离来更新从1到j的长度for(int j = 1 ; j <= n ; j ++ ){//dist[j] = Math.min(dist[j],dist[t] + g[t][j]);}}//如果最后n的长度没有改变，输出-1，没有找到；否则输出最短路nif(dist[n] == max) return -1;else return dist[n];}public static void main(String[] args){Scanner scan = new Scanner(System.in);n = scan.nextInt();m = scan.nextInt();//将他们每个点一开始赋值成一个较大的值for(int i = 1 ; i <= n ; i ++ ){Arrays.fill(g[i],max);}while(m -- > 0){int a = scan.nextInt();int b = scan.nextInt();int c = scan.nextInt();g[a][b] = Math.min(g[a][b],c);//这个因为可能存在重边，所以泽出最短的}int res = dijkstra();System.out.println(res);}
}

普通方法：bfs

import java.util.*;class Main {static int N = 510;static int[][] p = new int[N][N];public static void main(String[] args) {Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();for (int i = 0; i < p.length; i++) {Arrays.fill(p[i], 50000000);}for (int i = 0; i < m; i++) {int a = scan.nextInt();int b = scan.nextInt();int c = scan.nextInt();p[a][b] = Math.min(p[a][b],c);}int[] d = new int[N];Arrays.fill(d,(int)5e7);Queue<Integer> queue = new LinkedList<>();d[1] = 0;queue.add(1);while (queue.size() > 0) {int t = queue.poll();for (int i = 1; i <= n; i++) {if (p[t][i] != 50000000 && d[i] > d[t] + p[t][i]) {d[i] = d[t] + p[t][i];queue.add(i);}}}if (d[n] == 50000000) {System.out.print(-1);} else {System.out.print(d[n]);}}
}

7. 堆优化版dijkstra

在这里插入图片描述

13. Dijkstra求最短路 II（邻接表）

原题链接

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.PriorityQueue;public class Main{static int N = 100010;static int n;static int[] h = new int[N];static int[] e = new int[N];static int[] ne = new int[N];static int[] w = new int[N];static int idx = 0;static int[] dist = new int[N];// 存储1号点到每个点的最短距离static boolean[] st = new boolean[N];static int INF = 0x3f3f3f3f;//设置无穷大public static void add(int a,int b,int c){e[idx] = b;w[idx] = c;ne[idx] = h[a];h[a] = idx ++;}// 求1号点到n号点的最短路，如果不存在则返回-1public static int dijkstra(){//维护当前未在st中标记过且离源点最近的点PriorityQueue<PIIs> queue = new PriorityQueue<PIIs>();Arrays.fill(dist, INF);dist[1] = 0;queue.add(new PIIs(0,1));while(!queue.isEmpty()){//1、找到当前未在s中出现过且离源点最近的点PIIs p = queue.poll();int t = p.getSecond();int distance = p.getFirst();if(st[t]) continue;//2、将该点进行标记st[t] = true;//3、用t更新其他点的距离for(int i = h[t];i != -1;i = ne[i]){int j = e[i];if(dist[j] > distance + w[i]){dist[j] = distance + w[i];queue.add(new PIIs(dist[j],j));}}}if(dist[n] == INF) return -1;return dist[n];}public static void main(String[] args) throws IOException{BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));String[] str1 = reader.readLine().split(" ");n = Integer.parseInt(str1[0]);int m = Integer.parseInt(str1[1]);Arrays.fill(h, -1);while(m -- > 0){String[] str2 = reader.readLine().split(" ");int a = Integer.parseInt(str2[0]);int b = Integer.parseInt(str2[1]);int c = Integer.parseInt(str2[2]);add(a,b,c);}System.out.println(dijkstra());}
}class PIIs implements Comparable<PIIs>{private int first;//距离值private int second;//点编号public int getFirst(){return this.first;}public int getSecond(){return this.second;}public PIIs(int first,int second){this.first = first;this.second = second;}@Overridepublic int compareTo(PIIs o) {// TODO 自动生成的方法存根return Integer.compare(first, o.first);}
}

8. Bellman-Ford算法(遍历边)

14. 有边数限制的最短路

原题链接

b到1的距离 = min（a到1的距离 + a 到 b的距离）

import java.util.*;class Main {public static void main(String[] args) {Scanner scann = new Scanner(System.in);int n = scann.nextInt();int m = scann.nextInt();int k = scann.nextInt();int[] d = new int[n+2];Arrays.fill(d,0x3f3f3f3f);List<Edge> list = new ArrayList<>();for (int i = 0; i < m; i++) {int a = scann.nextInt();int b = scann.nextInt();int dist = scann.nextInt();Edge e = new Edge();e.a = a; e.b = b; e.d = dist;list.add(e);}d[1] = 0;for (int i = 0; i < k; i++) {int[] temp = Arrays.copyOf(d,d.length);for (Edge e : list) {int a = e.a;int b = e.b;int dist = e.d;if (temp[b] > d[a] + dist) {temp[b] = d[a] + dist;}}d = temp;}if (d[n] >= (int)0x3f3f3f3f/2) {System.out.print("impossible");} else {System.out.print(d[n]);}}static class Edge {int a;int b;int d;}}